Segment and Angle Addition: Your Complete Worksheet Guide

The world of geometry often revolves around understanding relationships between various shapes, lines, and angles. Among the most fundamental concepts for students to grasp are segment addition and angle addition. These principles are not only crucial for solving geometric problems but also for understanding the underlying mechanics of many mathematical proofs and real-world applications. In this guide, we'll delve deep into these topics, providing you with comprehensive worksheets that will boost your proficiency in geometry.
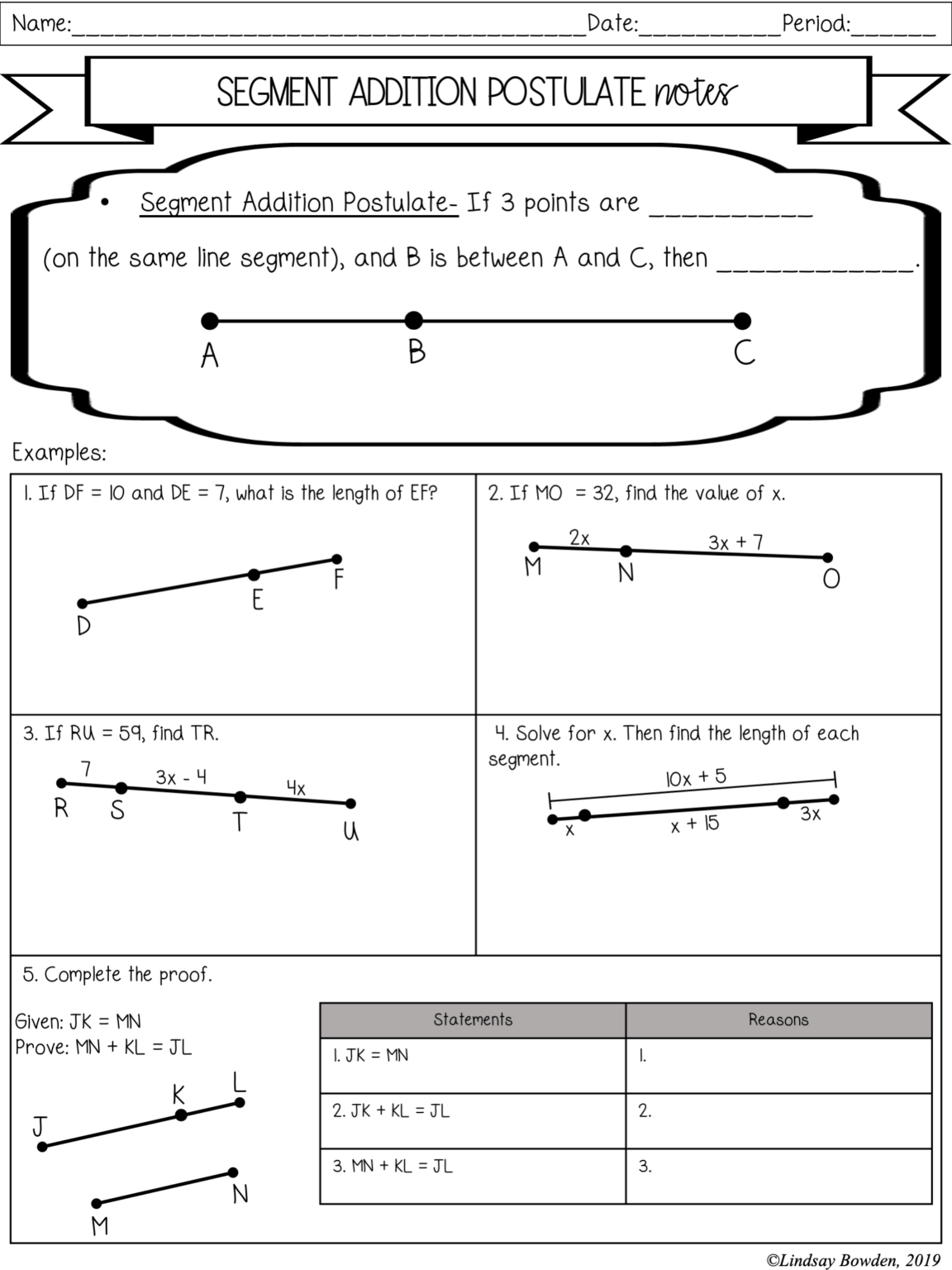
Understanding Segment Addition

Segment addition is the geometric principle that states if three points A, B, and C are collinear, with point B between A and C, then the total length of segment AC is the sum of the lengths of segment AB and BC. Mathematically, this can be expressed as:
- AB + BC = AC
This concept can be visually represented in diagrams, making it easier to solve problems related to lengths and distances. Here's an example:

To better understand this principle, here is a worksheet that you can practice:
| Problem | Solution |
|---|---|
| If AB = 5 cm and BC = 3 cm, what is AC? | AC = AB + BC = 5 cm + 3 cm = 8 cm |
| If AC = 10 cm and AB = 6 cm, what is BC? | BC = AC - AB = 10 cm - 6 cm = 4 cm |

📝 Note: Always ensure points are collinear and the middle point is between the other two.
Understanding Angle Addition

Angle addition involves adding the measures of adjacent angles to find the measure of a larger angle that encompasses both. If angle A and angle B share a common side and vertex, with angle B being adjacent to angle A, then:
- m∠A + m∠B = m∠C
Here's an illustrative diagram:

To practice this, you can use the following worksheet:
| Problem | Solution |
|---|---|
| If m∠A = 30° and m∠B = 45°, what is m∠C? | m∠C = m∠A + m∠B = 30° + 45° = 75° |
| If m∠C = 90° and m∠A = 40°, what is m∠B? | m∠B = m∠C - m∠A = 90° - 40° = 50° |
📝 Note: Adjacent angles share a vertex and a common side, but do not overlap.
Applying Segment and Angle Addition in Real-World Scenarios

Both segment and angle addition have numerous practical applications:
- Architecture and Construction: Understanding segment addition helps in calculating the total lengths of walls or beams. Angle addition is crucial in designing the angles of roofs or determining the correct alignment of walls.
- Surveying and Mapping: Surveyors use these principles to find exact distances between landmarks and to measure angles for accurate mapping.
- Art and Design: Artists and graphic designers apply these concepts when determining proportions and creating symmetrical designs or layouts.
Interactive Learning Tools

To further enhance your learning experience, consider using:
- GeoGebra: A dynamic mathematics software that allows you to create and manipulate geometric figures interactively.
- Online Geometry Games: Platforms like Khan Academy and Math Open Reference offer games that make learning segment and angle addition fun.
📝 Note: Interactive tools can provide instant feedback, which is invaluable for correcting and reinforcing understanding.
Advanced Problem-Solving

Let’s delve into some more complex problems that combine segment and angle addition:
| Problem | Solution |
|---|---|
| A triangle has side lengths AB = 7 cm, BC = 5 cm, and AC = 9 cm. Find the length of CD if D is a point on AB such that AD = 3 cm. | CD = AB - AD = 7 cm - 3 cm = 4 cm |
| In a quadrilateral, m∠A = 40°, m∠B = 120°, and m∠C = 70°. Find m∠D if ∠C and ∠D are supplementary. | m∠D = 180° - m∠C = 180° - 70° = 110° |
Worksheet Solutions for Deep Understanding

Below are further practice questions with solutions to help solidify your understanding:
| Problem | Solution |
|---|---|
| If segment XY = 15 units, and YZ = 10 units, what is XZ? | XZ = XY + YZ = 15 + 10 = 25 units |
| If m∠KLM = 60° and m∠MNP = 40°, with P on LM, what is the measure of ∠KLN? | m∠KLN = m∠KLM + m∠MNP = 60° + 40° = 100° |
The essence of mastering segment and angle addition lies not just in understanding these basic concepts but in applying them effectively to solve complex problems. By practicing with these worksheets and understanding the underlying principles, you'll be well-equipped to tackle more intricate geometric challenges. Remember, geometry isn't just about shapes; it's about understanding the relationships between parts of a whole, which is a fundamental skill in many areas of study and work.
Why is it important to understand segment and angle addition in geometry?

+
Understanding these concepts is crucial for problem-solving in geometry, especially for proofs involving lengths and angles. They are foundational for more advanced topics like coordinate geometry and trigonometry.
How can segment addition help in real life?
+
It’s used in various fields like architecture for determining distances, in computer graphics for rendering, and even in everyday situations like cutting fabric for sewing or planning space in a room.
Can you recommend some interactive resources for practicing angle addition?

+
Interactive tools like GeoGebra, Desmos, and the “Geometry Playground” on Khan Academy are excellent for visualizing and practicing angle addition in an engaging way.
What’s the difference between segment addition and angle addition?

+
Segment addition involves adding lengths of collinear segments, while angle addition involves adding measures of adjacent angles to find the measure of a larger encompassing angle.