5 Essential Tips for Mastering Scientific Notation

Understanding Scientific Notation

Before we delve into the specifics, let’s ensure we grasp what scientific notation is. This mathematical notation simplifies the way we write very large or very small numbers, making them more manageable for calculations or visual representation. Scientific notation expresses numbers as a product of two factors: a coefficient (ranging from 1 to less than 10) and a power of 10 exponent. Here’s how it works:
- Coefficient: A number between 1 and 10 (inclusive of 1, exclusive of 10).
- Power of 10: An exponent (denoted as ‘e’ or ‘×10^’) that signifies how many places the decimal point must move to form the number in standard decimal form.
Tip 1: Learn to Recognize When to Use It


Scientific notation is incredibly useful when dealing with:
- Very large numbers: such as the distance to celestial bodies or the population size of microorganisms.
- Very small numbers: like the mass of an electron or the time it takes for a chemical reaction to occur.
- Data comparison and analysis where standard notation might be cumbersome.
- Mathematical operations where standard notation could lead to significant figure errors.
Tip 2: Practice Converting to and from Scientific Notation

The key to mastering scientific notation is to become proficient in converting numbers:
- To Scientific Notation:
- Determine the decimal point’s initial position.
- Move the decimal point to the right or left to make it between 1 and 10.
- Count the number of places the decimal was moved and use this as the exponent.
- Add or subtract this number from the coefficient depending on the direction of movement.
- From Scientific Notation:
- Take the coefficient and move the decimal point left or right according to the exponent.
- If the exponent is positive, move the decimal point to the right; if negative, to the left.
- Replace the ‘×10^’ with zeros if necessary to reflect the actual number.
💡 Note: When moving the decimal point, ensure you keep track of the number of places it moves as this affects the exponent.
Tip 3: Understand the Rules for Operations

Operations in scientific notation follow specific rules to maintain accuracy:
- Multiplication: Multiply the coefficients and add the exponents.
- Division: Divide the coefficients and subtract the exponents.
- Addition/Subtraction: Convert numbers to have the same power of 10 (through adjustment of the decimal), then perform the operation on the coefficients.
⚙️ Note: Remember that when adding or subtracting, converting to the same exponent ensures accuracy in the coefficient manipulation.
Tip 4: Know the Decimal Rules

The placement of the decimal in scientific notation is crucial:
- When converting a number greater than or equal to 10 to scientific notation, move the decimal left until the coefficient is between 1 and 10, and use a positive exponent.
- For numbers less than 1, move the decimal to the right until the coefficient is between 1 and 10, and use a negative exponent.
Here’s a table to illustrate:
| Number | Scientific Notation |
|---|---|
| 1200 | 1.2 × 10^3 |
| 0.0045 | 4.5 × 10^-3 |

Tip 5: Practice with Real-World Examples

Engage with scientific notation through practical examples:
- The speed of light in a vacuum is approximately 299,792,458 meters per second or 2.99792458 × 10^8 m/s.
- The mass of the earth is about 5.97219 × 10^24 kilograms.
This practice will reinforce your understanding and make scientific notation second nature.
By mastering these essential tips, you'll unlock the power of scientific notation. It simplifies dealing with extreme values, which is particularly useful in scientific and mathematical fields. From understanding fundamental concepts to executing operations with confidence, these tips are your key to seamless navigation through numbers that stretch beyond everyday comprehension. Remember, practice and application are key to internalizing scientific notation, allowing you to communicate complex data with ease.
Why is scientific notation useful?

+
Scientific notation helps simplify the representation of very large or very small numbers, making it easier to perform mathematical operations and comparisons.
How do you add numbers in scientific notation?

+
When adding numbers in scientific notation, first ensure that the exponents are the same. Convert one number if necessary, then add the coefficients directly.
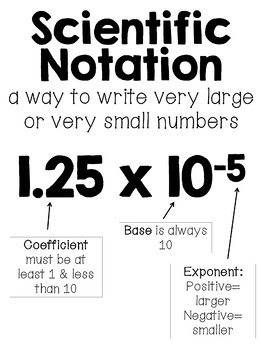
What does a negative exponent mean in scientific notation?
+
A negative exponent indicates that the number in decimal form will be less than one, moving the decimal point to the left.