5 Essential Tips for Rounding to Significant Figures

When dealing with numbers in science and engineering, the concept of significant figures becomes crucial. Rounding to the correct number of significant figures is not just about simplifying numbers; it's about maintaining precision where it matters. This detailed guide will explore five essential tips to master rounding to significant figures effectively, enhancing both accuracy and presentation in your numerical reports and calculations.

1. Understand the Basics of Significant Figures

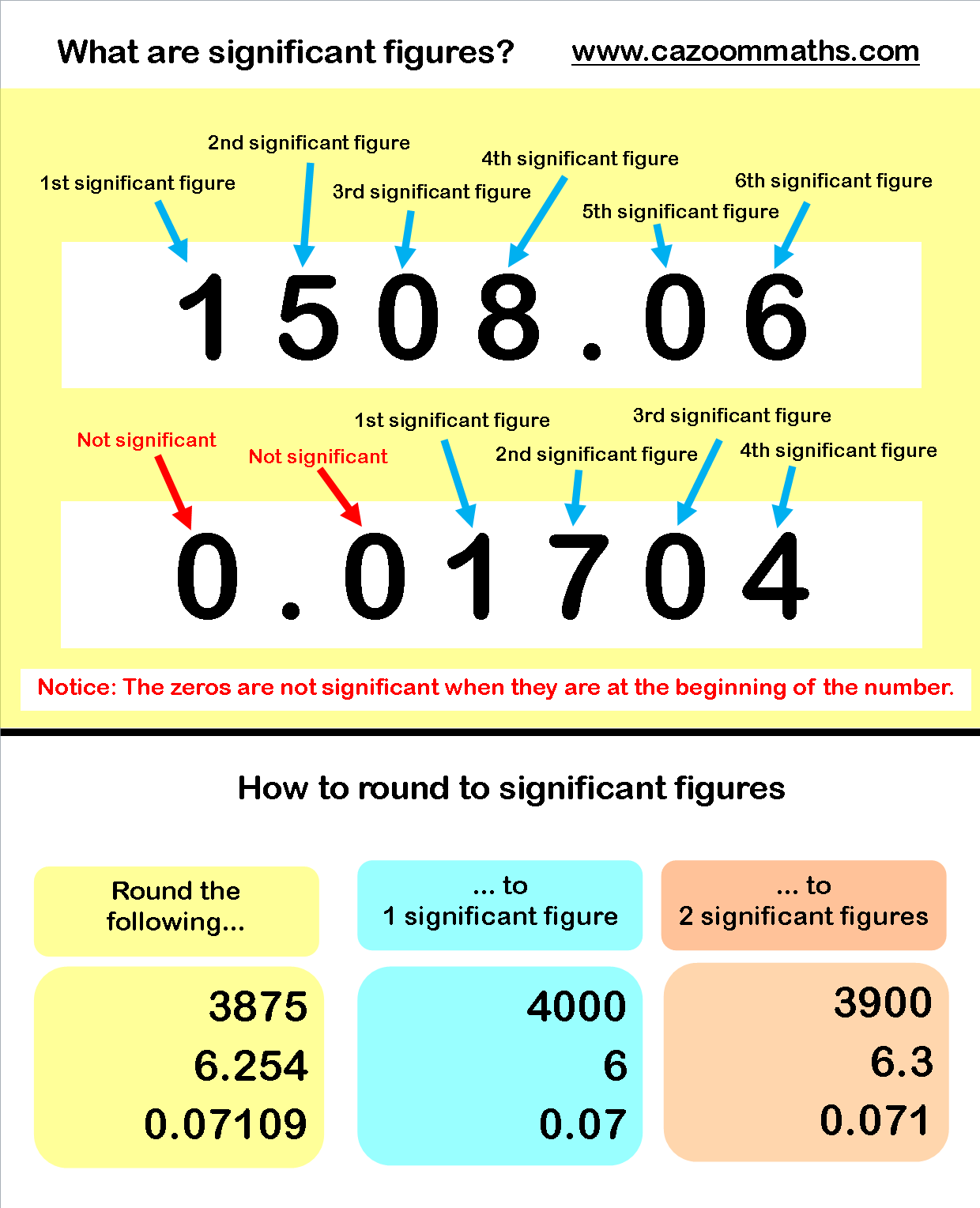
Significant figures (sig figs) represent the digits in a number that carry meaning in terms of precision. Here’s a breakdown:

• All non-zero digits are significant. For example, 345 has three significant figures.
• Zeros between non-zero digits are significant. Like in 503, the zero is significant, making the number three significant figures.
• Zeros before the decimal point in numbers less than 1 are not significant. For example, 0.0025 has two significant figures.
• Zeros at the end of a number without a decimal point are ambiguous. To clarify, use scientific notation; for example, 200 has one significant figure unless written as 2.00 x 10², where it has three.

2. The Art of Rounding

The process of rounding to a specific number of significant figures involves:

• Identifying the position of the last significant figure.
• If the next digit to this position is 5 or greater, round up the last significant figure.
• If it’s less than 5, leave the last significant figure unchanged.

Let’s illustrate with an example:

When rounding 34.678 to three significant figures, the number 4 is our focus. Since 6 follows, we round up:

3. Dealing with Zeros in Rounding

Rounding to significant figures often involves decisions about trailing zeros:

• Keep trailing zeros after rounding to maintain clarity: If you round 2350 to two significant figures, you might write 2400 to show it’s rounded, not an exact number.
• Use decimal points when necessary: To avoid ambiguity, write 24.0 instead of 24 when rounding 24.16 to two significant figures.

🔍 Note: Writing numbers in scientific notation can eliminate confusion about trailing zeros and improve the precision of your figures.

4. Rounding Calculations

In a series of calculations involving multiple steps, follow these rules:

• After each step, round to the least number of significant figures involved: If you multiply 2.15 (three sig figs) by 3.0 (two sig figs), the result should have only two significant figures, which is 6.5.
• However, retain extra digits until the final calculation: Keep extra digits during intermediate steps to minimize rounding errors. Only round to the least number of significant figures at the end.

5. Verification and Consistency

Always check your work:

• Use scientific calculators that can set the number of significant figures or manually verify your results.
• Be consistent in the presentation of your results. If you’re working within a team or reporting data, ensure everyone is rounding in the same way to maintain consistency.

The practice of rounding to significant figures is integral to accurate data representation. By mastering these tips, you'll ensure that your work reflects both precision and clarity in numeric representation. Remember, precision in your data helps to tell a more accurate story, fostering trust in the results you present.

Why is it important to round to significant figures?

+

Rounding to significant figures ensures the precision of your measurements or calculations is accurately conveyed. It helps in eliminating unnecessary digits, making the data easier to read and understand.

What if I have a number like 100,001?

+

The trailing 1 is the most significant, making the number six significant figures. If rounding to three significant figures, it would become 100,000.

Can significant figures change with scientific notation?

+

Scientific notation doesn’t change the number of significant figures; it only changes how the number is written. For example, 200 can be 2 x 10² with one significant figure or 2.00 x 10² with three, depending on how it’s interpreted or presented.