Master Rotation: 90 Degrees Counterclockwise Worksheet

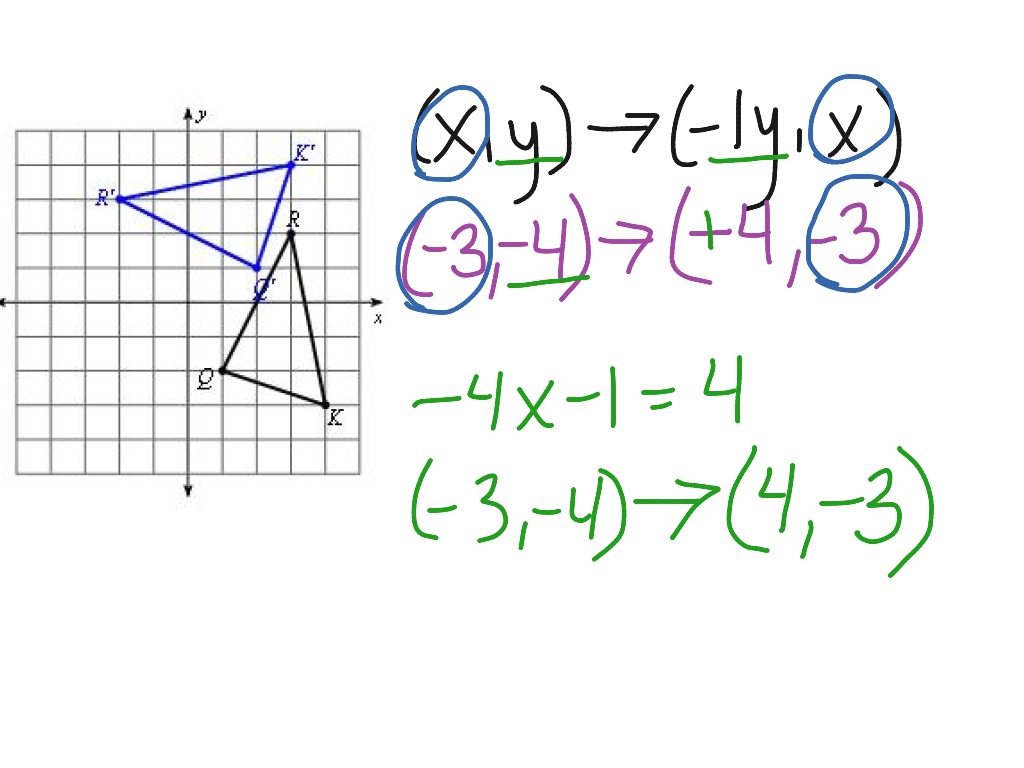
Understanding the Concept of 90 Degrees Counterclockwise Rotation

The concept of rotating a point or an object 90 degrees counterclockwise involves a fundamental geometric transformation where each point or vertex is moved around a pivot point in such a manner that the angle between its initial position and its new position is 90 degrees less than the original. This type of rotation can be visualized on a coordinate plane where you move points, lines, or shapes from their original positions to new positions at a right angle to their starting points.

In geometry, this transformation is vital for understanding not just the orientation but also the spatial relationships between different objects or points. Here's how it works:

• The x-coordinates become the y-coordinates and the y-coordinates become the negative of the original x-coordinates.
• The origin (0,0) serves as the center of rotation.

Step-by-Step Guide to Performing a 90-Degree Counterclockwise Rotation

To illustrate the process, let's rotate a point (x, y) by 90 degrees counterclockwise:

1. Identify the initial coordinates of the point or shape you wish to rotate.
2. Take the current x-coordinate and make it the new y-coordinate.
3. Take the current y-coordinate, negate it, and make it the new x-coordinate.
4. The new point after rotation will be (-y, x).

Example:

Consider a point (2, 3). Applying the 90-degree counterclockwise rotation:

• The new x-coordinate would be -3 (negative of the original y-coordinate).
• The new y-coordinate would be 2 (original x-coordinate).

The new coordinates are now (-3, 2).

Practical Application of 90-Degree Counterclockwise Rotation

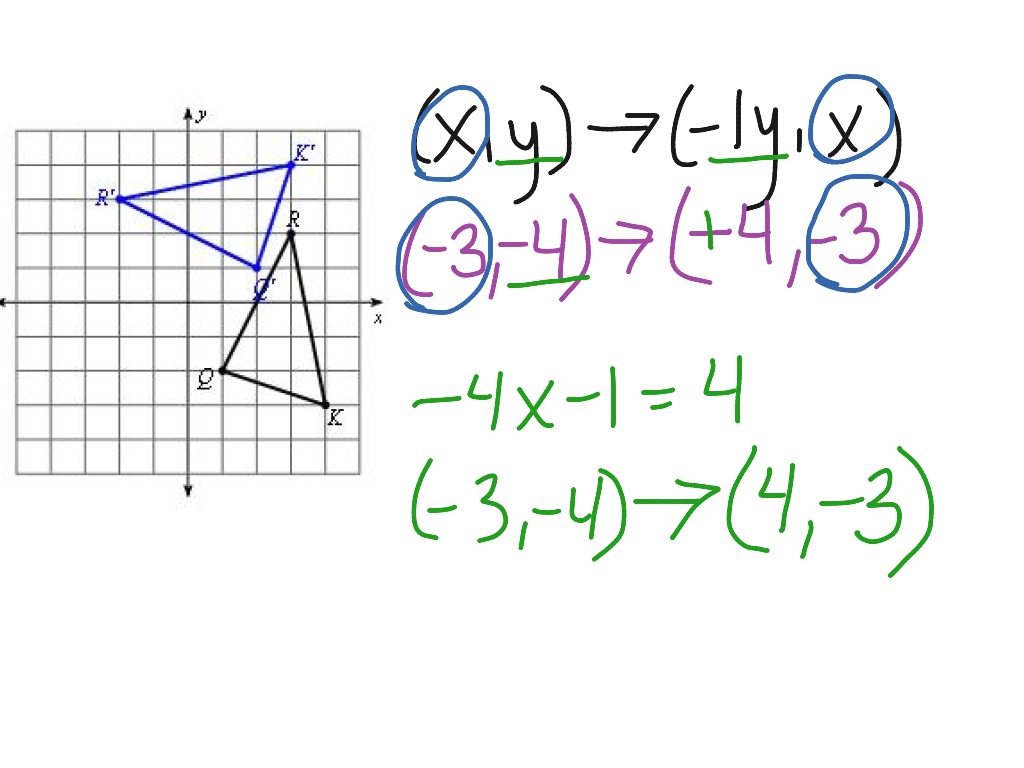
Let's delve into how this transformation can be applied:

Rotating Shapes

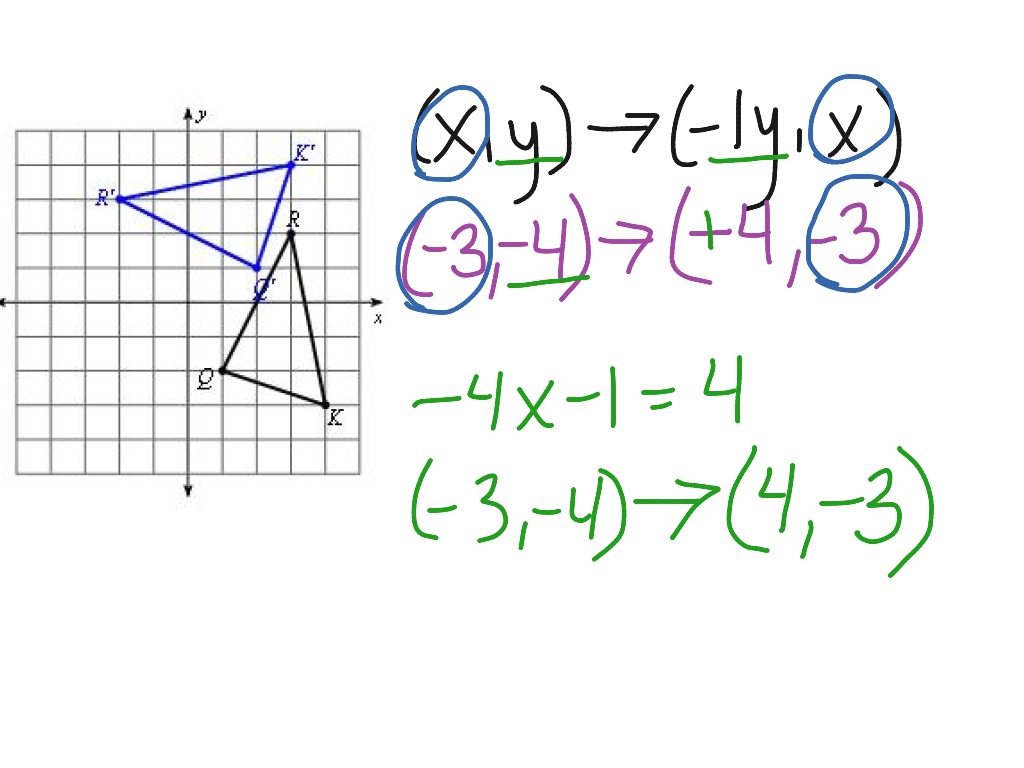
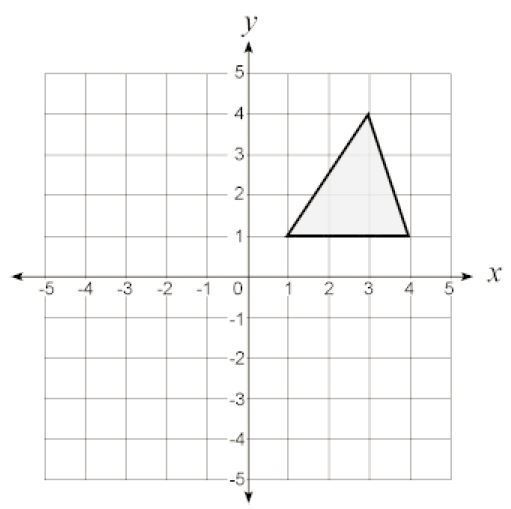
When rotating a shape like a triangle or a square, each vertex undergoes this transformation:

• If (A(1,4), B(5,4), C(3,2)) are the vertices of a triangle:
• Rotate A: (1,4) becomes (-4, 1)
• Rotate B: (5,4) becomes (-4, 5)
• Rotate C: (3,2) becomes (-2, 3)

The rotated triangle will have new coordinates (-4, 1), (-4, 5), and (-2, 3).

Rotating Axes

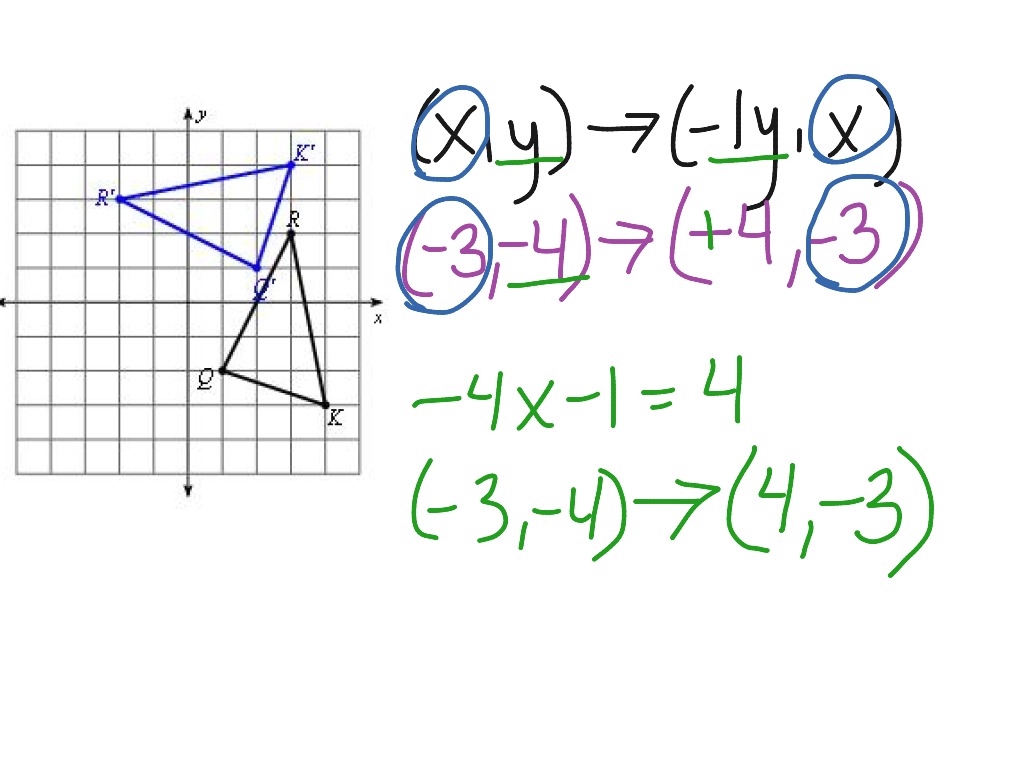
Understanding rotation can also extend to axes:

• Rotate the x-axis by 90 degrees counterclockwise; it becomes the y-axis.
• Similarly, rotate the y-axis to get a negative x-axis.

Creating a 90 Degrees Counterclockwise Rotation Worksheet

A worksheet designed to practice this concept could include the following components:

Exercises:

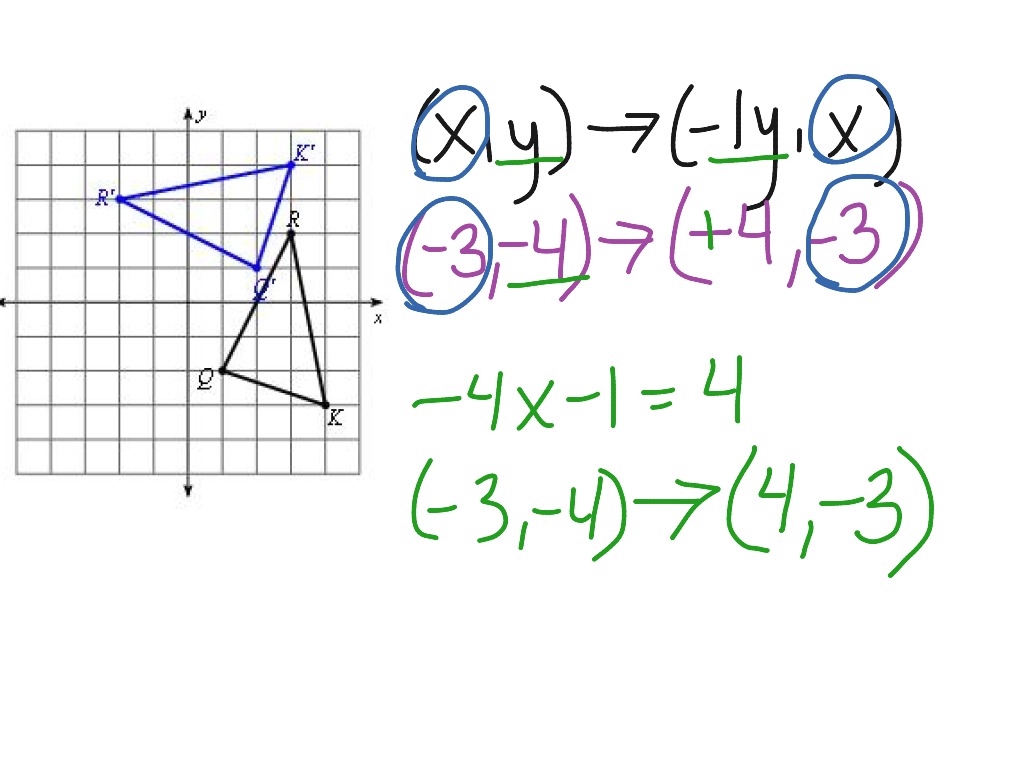
• Rotate simple points to understand the transformation better.
• Rotate shapes and compare original and rotated shapes.
• Draw rotations with given points or shapes.

Blank Coordinate Grids:

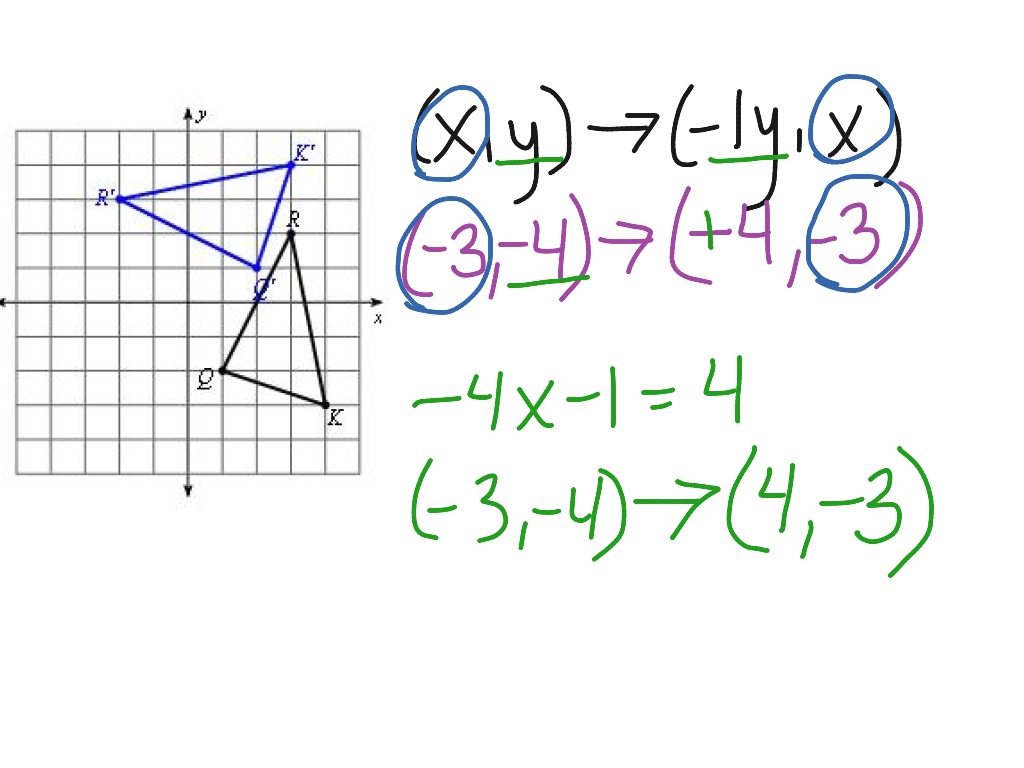
These are essential for students to perform their rotations and visualize the result:

Important Notes

✨ Note: Remember that when you rotate points or shapes counterclockwise, the orientation of your shape might appear reversed if you are using a mirror or are looking from the other side.

Incorporating a 90 degrees counterclockwise rotation worksheet into your teaching or learning can significantly enhance spatial awareness and the understanding of geometric transformations. By engaging with such exercises, students and enthusiasts can develop a more profound comprehension of how objects move in space, which is crucial for fields like engineering, computer graphics, and various branches of applied mathematics.

As we wrap up this exploration of 90-degree counterclockwise rotation, it's clear that this transformation is not just a simple shift but a fundamental aspect of geometric reasoning. Understanding how to rotate points and shapes around a pivot point, whether it's the origin or another designated point, opens up a world of spatial manipulation and design, equipping learners with the tools to navigate both abstract and real-world problems where such transformations play a key role.

What happens to the x and y coordinates in a 90-degree counterclockwise rotation?

+

In a 90-degree counterclockwise rotation, the x-coordinate becomes the y-coordinate, and the y-coordinate becomes the negative of the original x-coordinate. The new coordinates of a point (x, y) would be (-y, x).

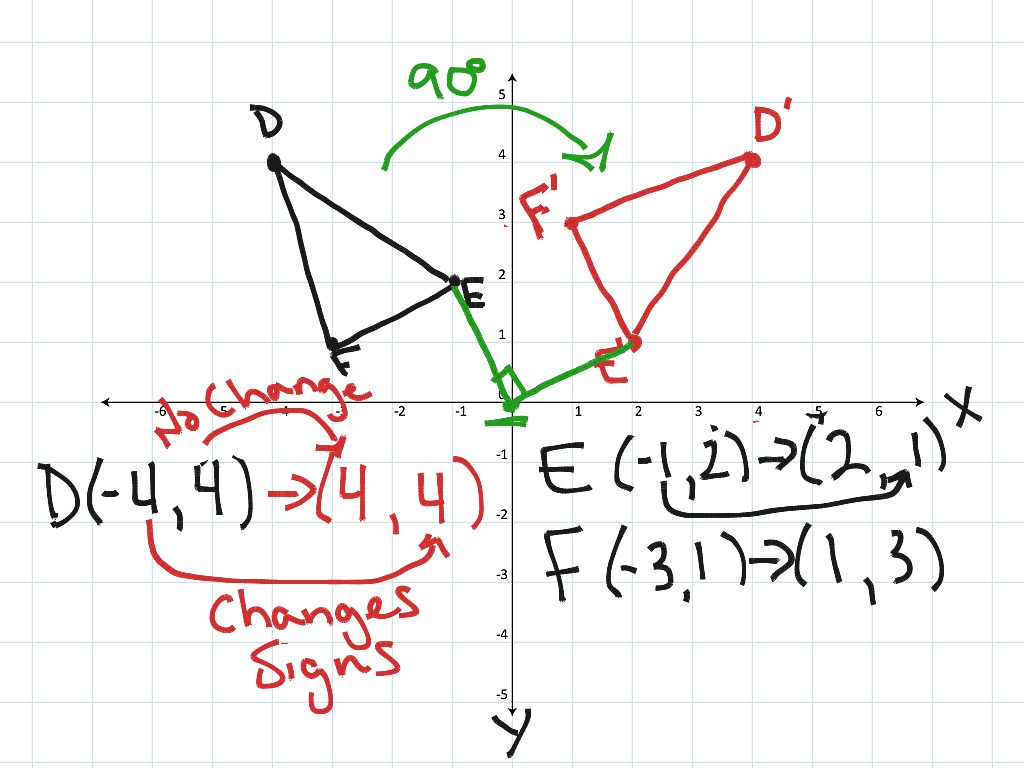
Can shapes be rotated by 90 degrees counterclockwise?

+

Yes, entire shapes can be rotated by applying the same transformation rules to each vertex of the shape. For example, each vertex of a triangle or square would be rotated using the formula (-y, x).

Is the 90-degree counterclockwise rotation the same as the 270-degree clockwise rotation?

+

Yes, rotating an object 270 degrees clockwise results in the same final position as rotating it 90 degrees counterclockwise. Both transformations essentially achieve the same end result.