Master Rise Over Run with Answer Worksheets
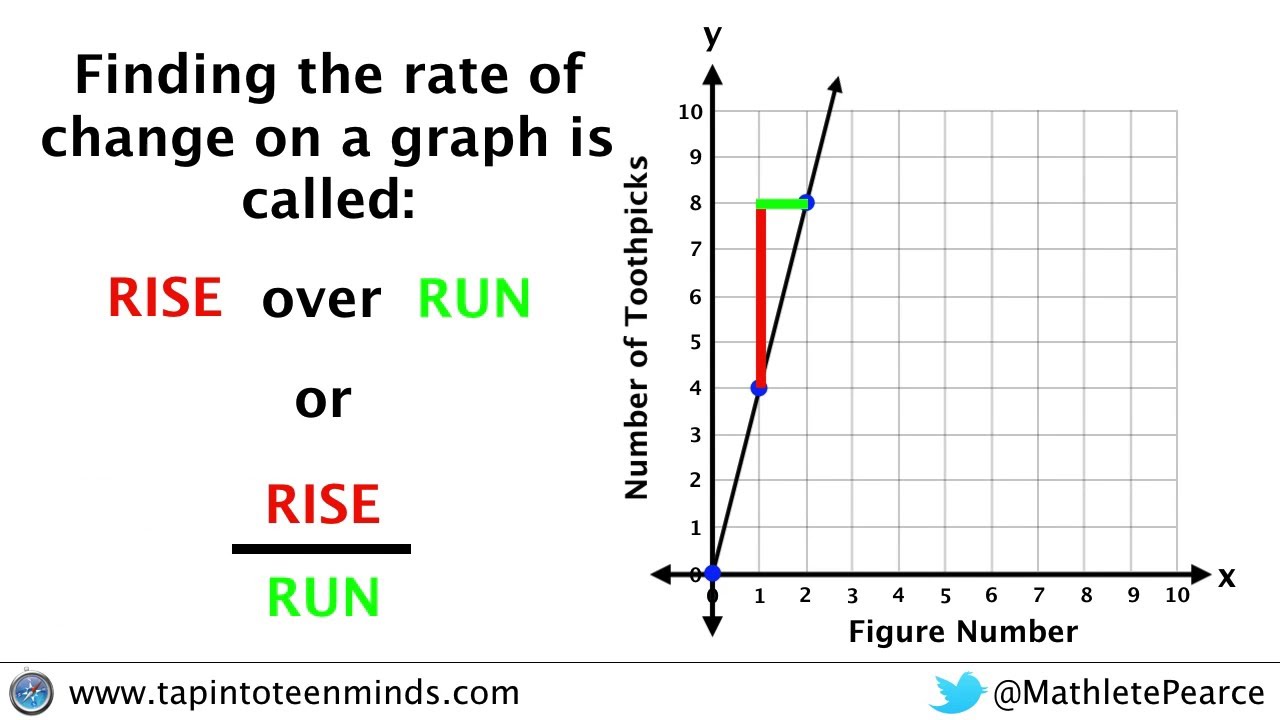
Understanding the concept of slope or 'rise over run' is fundamental in mathematics, especially when you delve into areas like algebra, geometry, and even calculus. The slope defines how steep a line is, which is vital in real-world applications such as designing infrastructure, analyzing trends, or simply solving everyday problems. Let's explore this concept in depth with practical examples and exercises in this blog post.
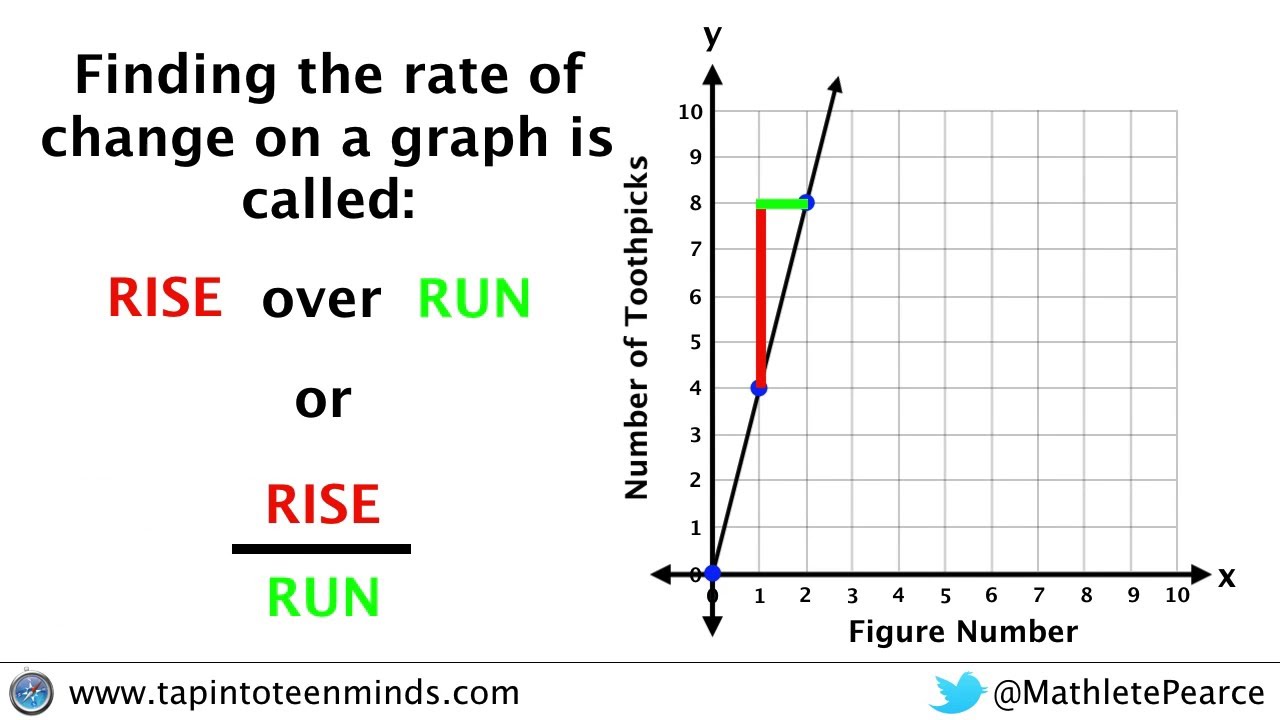
What is Rise Over Run?

Rise over run is a way to express the slope of a line. Here’s how it works:
- Rise: The vertical distance between two points on the line.
- Run: The horizontal distance between those same two points.
The slope (m) of a line can be calculated using the formula:
[ m = \frac{\text{Rise}}{\text{Run}} ]Let's look at a simple example to understand this better:
- If point A is at (2, 3) and point B is at (4, 5), then:
- The rise (vertical distance) from A to B is 5 - 3 = 2.
- The run (horizontal distance) from A to B is 4 - 2 = 2.
- So, the slope m = \frac{2}{2} = 1 .
Calculating Slope from Graphs

When you have a graph, calculating the slope is as straightforward as looking at the lines:
| Line Type | Slope Description | Example |
|---|---|---|
| Horizontal line | Slope is 0 | y = 3 (no change in y-values) |
| Vertical line | Slope is undefined | x = -2 (no change in x-values) |
| Positive Slope | Rising from left to right | y = 2x + 3 (up 2, right 1) |
| Negative Slope | Falling from left to right | y = -3x + 4 (down 3, right 1) |

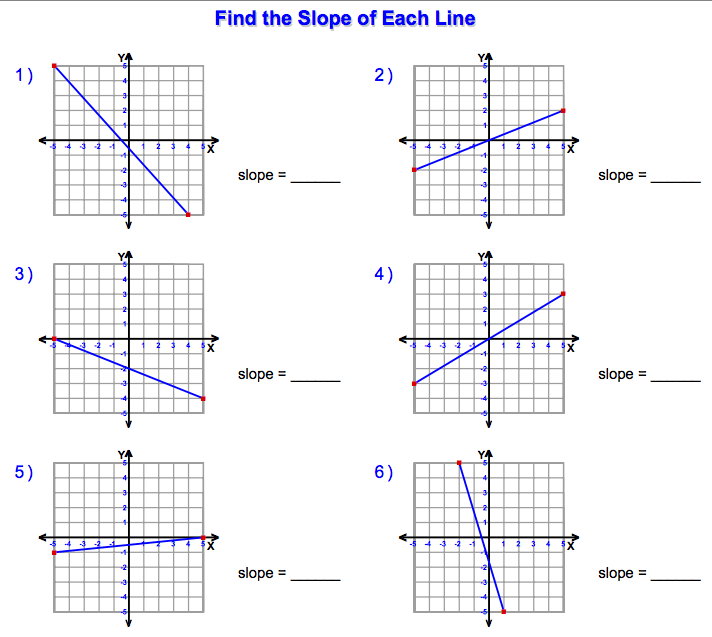
Worksheets for Slope Calculation

To solidify your understanding, let’s go through some exercises. Here’s how you can tackle these worksheets:
- Choose two points: From a line on the graph, select any two points.
- Calculate the rise: Subtract the y-coordinates (y2 - y1).
- Calculate the run: Subtract the x-coordinates (x2 - x1).
- Divide: Divide the rise by the run to get the slope.
📝 Note: If you're working on a worksheet, make sure to label your answers clearly.
Real-Life Applications of Slope
The concept of slope isn’t just an academic exercise; it has real-world implications:
- Architecture: Slope determines the pitch of a roof, affecting drainage and stability.
- Engineering: In transportation, gradients and slopes are crucial for road design, track alignments, etc.
- Economics: To understand how variables like price and demand change relative to each other.
Positive vs. Negative Slopes
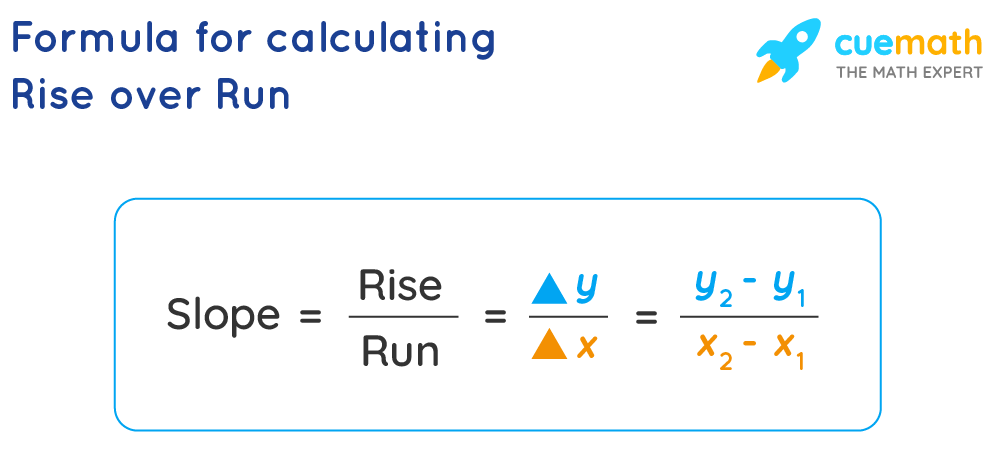
Understanding the behavior of a line:
- Positive Slope: As x increases, y increases. This indicates an upward trend.
- Negative Slope: As x increases, y decreases. This shows a downward trend.
To sum up, the concept of rise over run or slope is a fundamental tool in mathematics, offering insights into the relationship between two variables. Whether you're working through worksheets or applying the concept in real-life scenarios, understanding slope will make you adept at interpreting and analyzing graphical data. Always remember, slope helps us navigate the mathematical landscape with precision and clarity.
What does a slope of 0 mean?
+
A slope of 0 means that the line is horizontal, and there is no change in the y-value as you move along the x-axis. All points on this line share the same y-coordinate.
Can slope be negative?
+
Yes, a negative slope means that the line is falling or descending from left to right. This indicates a decreasing trend where y decreases as x increases.
Why is understanding slope important in real life?

+
Slope is vital for understanding rates of change, designing physical structures, optimizing travel routes, and interpreting data trends in various fields.