Master Right Triangle Trigonometry with Our Free Worksheet

In the field of mathematics, trigonometry holds a unique place, especially when it comes to understanding right-angled triangles. These triangles are not just fundamental for basic geometry but also for various scientific and engineering applications, from calculating heights and distances to designing safe and sturdy structures. Whether you're a high school student, an engineer, or a hobbyist in mathematics, mastering trigonometry is pivotal. Here, we'll explore the art of trigonometry through a free, comprehensive worksheet that helps you grasp the core concepts in an interactive manner.
Understanding Trigonometric Ratios

Let’s start at the root, which is understanding the three fundamental trigonometric ratios:
- Sine (sin): Opposite / Hypotenuse
- Cosine (cos): Adjacent / Hypotenuse
- Tangent (tan): Opposite / Adjacent
These ratios are the backbone of trigonometry:
| Angle | Sin | Cos | Tan |
|---|---|---|---|
| 30° | 0.5 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 0.5 | √3 |
🔍 Note: These ratios are for right-angled triangles, and the hypotenuse is always the longest side.
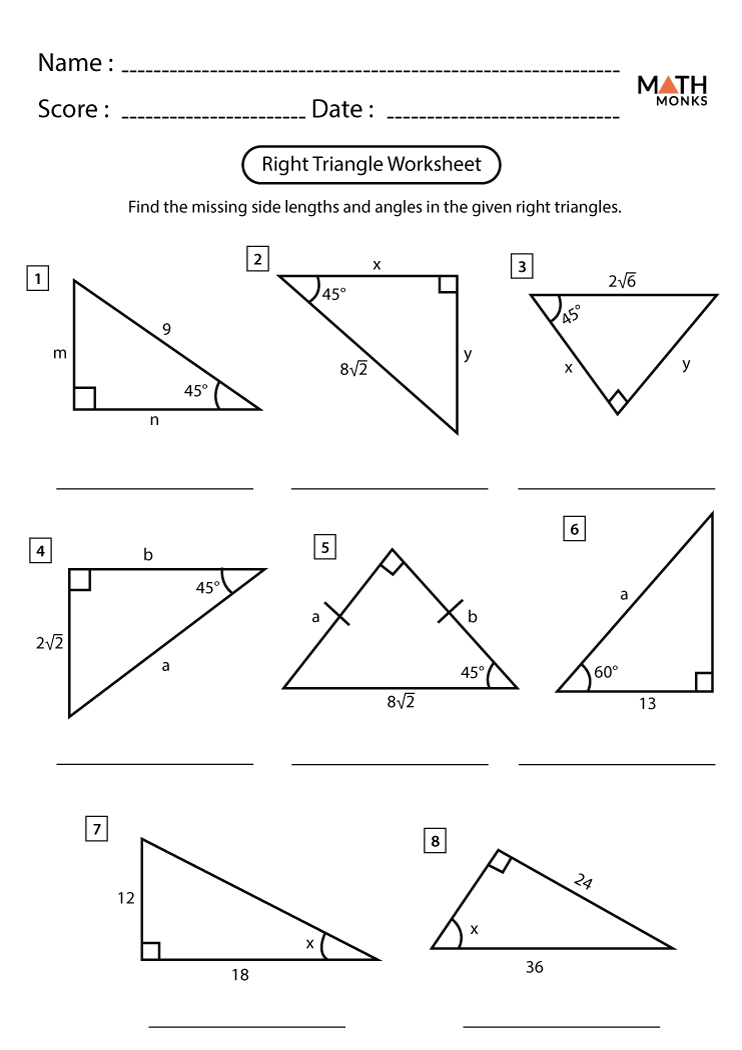
Interactive Trigonometry Worksheet
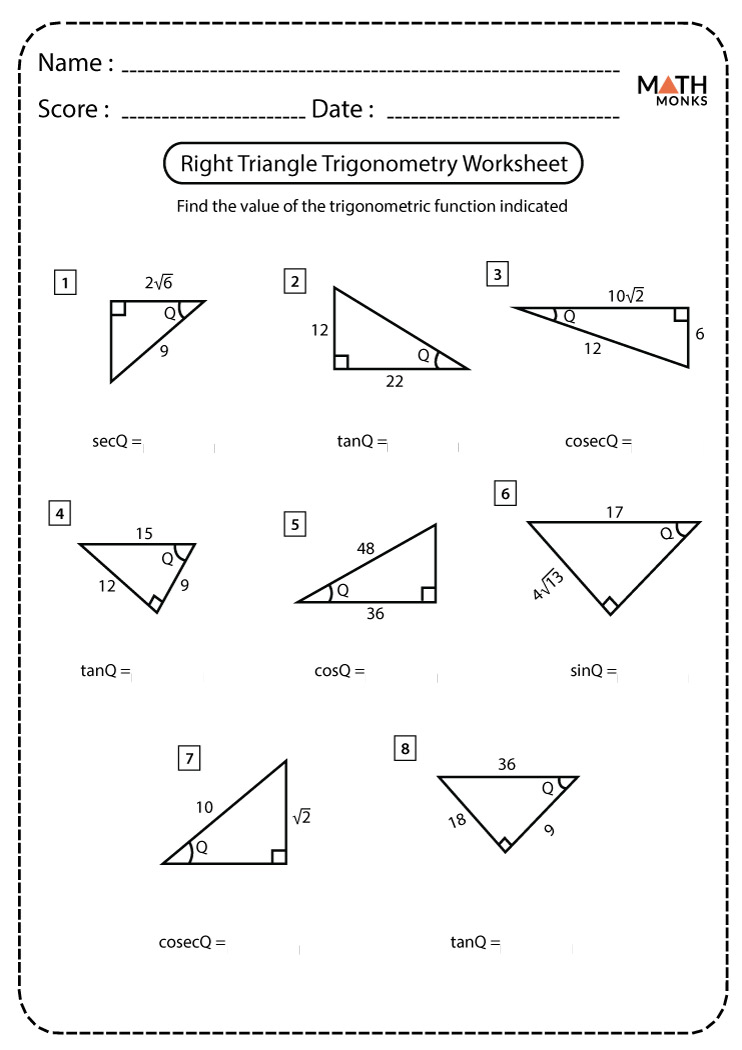
Our worksheet is designed to reinforce these ratios through practical exercises:
- Solving for unknown sides using trigonometric ratios.
- Calculating angles from known sides.
- Using the pythagorean theorem in conjunction with trigonometric functions.
The worksheet includes:
- Diagrams of various right triangles for visual reference.
- Problems ranging from basic to more complex scenarios.
- Worked examples to guide you through the solutions.
Practical Applications

The real-world application of trigonometry in right triangles is vast:
- Architecture: Calculating the height of a building or roof pitch.
- Surveying: Determining land elevations and distances.
- Navigation: Determining distances and positions, especially useful in aviation and maritime navigation.
Advanced Trigonometric Concepts

Once the basics are understood, students can dive into more advanced topics:
- Trigonometric identities like sin²(x) + cos²(x) = 1.
- The use of inverse trigonometric functions to find angles from trigonometric ratios.
- Pythagorean theorem's relationship with trigonometric ratios.
Each of these areas expands the toolset for solving more complex problems.
How to Utilize the Worksheet Effectively

To get the most out of your trigonometry worksheet, consider these strategies:
- Step-by-Step Approach: Work through each problem systematically, writing down the steps you’re using.
- Check Your Work: Always verify your answers using multiple methods or the provided solutions.
- Revise: Go back to the worksheet periodically to refresh your memory on the key concepts.
- Collaborate: Work in groups to discuss and solve problems for a deeper understanding.
Your journey through the world of trigonometry using our worksheet will not only make these abstract concepts tangible but will also enhance your problem-solving skills.
Understanding right triangles and their trigonometry is not just about solving problems for a math class. It's about grasping a fundamental aspect of geometry that plays a critical role in countless real-world scenarios. With practice, patience, and our comprehensive worksheet, you can master this essential area of mathematics, applying it confidently in various fields.
Why are right triangles so important in trigonometry?

+
Right triangles are essential in trigonometry because the ratios of their sides (sine, cosine, tangent) form the basis for all trigonometric functions, enabling us to calculate lengths, angles, and solve real-world problems involving angles.
How can I improve my understanding of trigonometric ratios?

+
To enhance your understanding, practice frequently, use visualization aids like diagrams, and relate ratios to real-world applications. Regularly solving different problems will reinforce these concepts.
What are the real-world applications of trigonometry?

+
Trigonometry is applied in architecture for designing structures, in surveying to measure land, in navigation for calculating distances, and in engineering and physics for solving problems involving forces and angles.



