5 Essential Rhombus Properties Worksheet Tips

A rhombus, often mistaken for a diamond shape, has some very distinct properties that set it apart in the world of geometry. Understanding these properties is not just fascinating but can also be quite useful, especially when you're solving mathematical puzzles or designing intricate patterns in fields like architecture or art. Here, we've compiled a worksheet with tips to help you master the essential properties of a rhombus. Let's dive right in.
Tip 1: All Sides are Equal


One of the most fundamental properties of a rhombus is that all its sides are of equal length. This means if you measure one side, you automatically know the length of all four sides. This characteristic is especially useful when you’re solving geometric problems involving rhombi or when you’re using rhombi in design:
- Measure one side to get the perimeter.
- Use the side length to calculate the height if the diagonals are known.
Tip 2: Opposite Angles are Equal
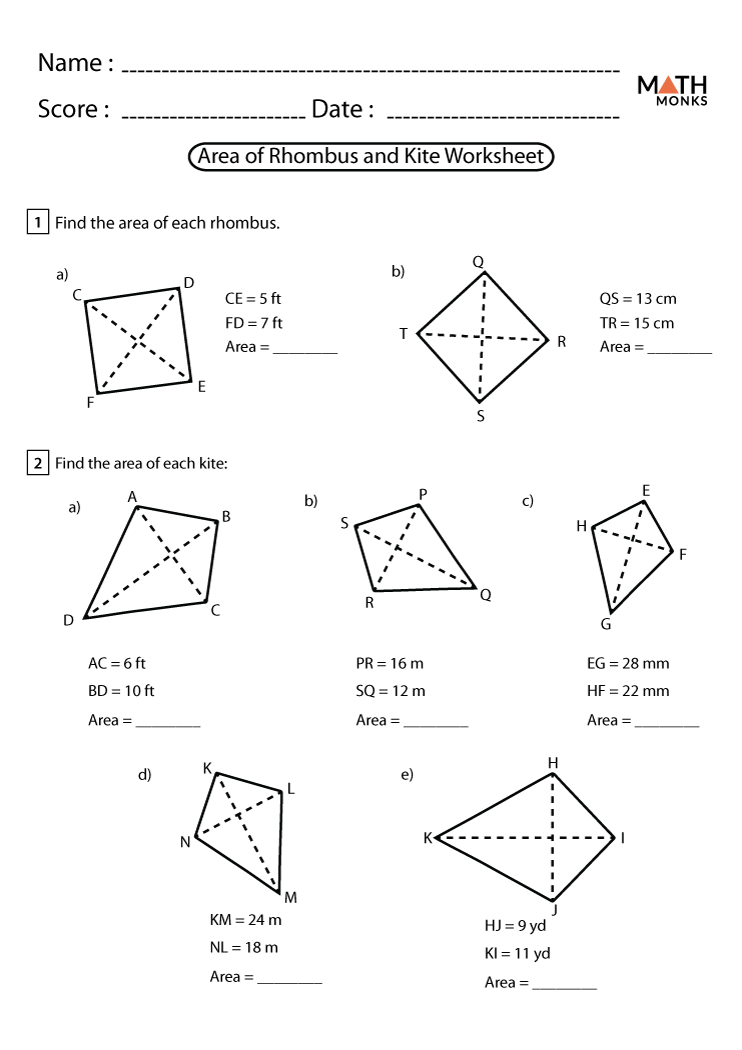
The rhombus has a unique symmetry where opposite internal angles are equal. This property makes rhombi particularly appealing for symmetry-based designs:
- Identify one angle to know the opposite angle instantly.
- Angles at the ends of the same diagonal are supplementary (sum up to 180 degrees).
Tip 3: Diagonals Bisect Each Other at Right Angles


This tip might seem basic, but its implications are profound. The diagonals of a rhombus not only bisect each other but do so at 90 degrees. Here’s how this property comes into play:
- Helps in finding the area of a rhombus when the lengths of the diagonals are known.
- Provides a framework for constructing perfect right angles in various applications.
Tip 4: Understanding the Symmetry

⭐ Note: Knowing the symmetry is crucial for solving problems related to rhombus and for creating symmetrical patterns in art.
A rhombus exhibits rotational symmetry of 180 degrees, which means you can rotate the shape by 180 degrees, and it will still look the same. Here's how this symmetry helps:
- Simplifies the calculation of angles within the rhombus.
- Assists in visualizing and sketching rhombi accurately.
| Property | Significance |
|---|---|
| Symmetry at 180 degrees | Facilitates sketching and solving rhombus-based problems. |

Tip 5: Identifying and Constructing Rhombi


To identify or construct a rhombus, you only need to ensure four sides are of equal length, and the opposite angles are equal. This tip is vital when you are working with limited information or constructing geometric shapes:
- Use a ruler to measure four sides.
- Verify the opposite angles to confirm the shape.
💡 Note: Sometimes, identifying a rhombus can be tricky in real-world scenarios where measurements might not be perfectly precise.
To sum up, by understanding and applying these key properties of a rhombus, you can significantly enhance your problem-solving skills in geometry. Whether you're tackling intricate math problems, designing, or simply exploring the beauty of geometric shapes, these worksheet tips provide a robust foundation to work from. These properties not only define what makes a rhombus unique but also show how this shape can be used effectively in various applications.
What makes a shape a rhombus?

+
A shape is a rhombus if all its four sides are equal in length, and the opposite angles are congruent. These characteristics distinguish a rhombus from other parallelograms.
Can a square be considered a rhombus?

+
Yes, a square is a special kind of rhombus. It has all the properties of a rhombus, plus all angles are right angles (90 degrees), making it a perfect example of how a rhombus can have additional properties.
How do you calculate the area of a rhombus?

+
There are several ways to calculate the area of a rhombus: - Using diagonals: Multiply half the lengths of the diagonals and then multiply by 2 (since diagonals bisect at right angles). - Using base and height: Simply base (side length) times height. - Using side and an angle: Using the formula: A = (a^2) * sin(θ), where a is the side length and θ is one of the angles.
Are all rhombi parallelograms?

+
Yes, all rhombi are parallelograms by definition because opposite sides are parallel and equal in length. However, not all parallelograms are rhombi, as not all have all sides equal.