5 Essential Tips for Mastering Slope Worksheets
Conquering slope worksheets can often feel like navigating a steep hill, but with the right approach and tools, you can turn this task into a manageable and even rewarding experience. Whether you're a student aiming to ace your math exams, a tutor seeking effective teaching strategies, or someone who just loves algebra, mastering slope worksheets is key to understanding linear equations and functions. Here are five essential tips to help you ascend the challenge of slope worksheets with confidence.
Practice Identifying Types of Slopes
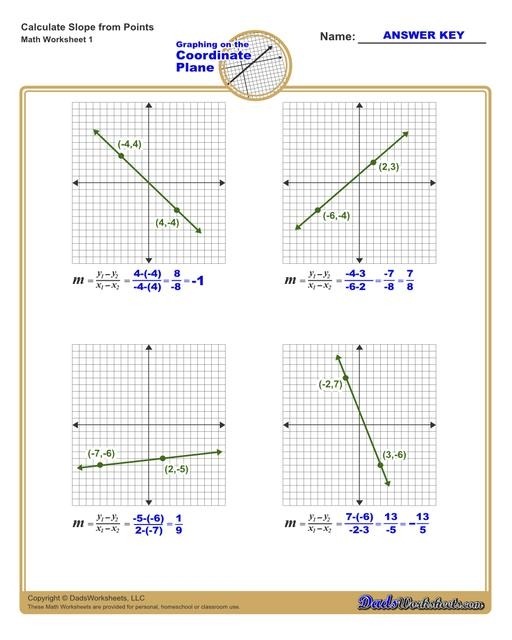

Slopes come in four main types: positive, negative, zero, and undefined. Here’s how to identify each:
- Positive Slope: The line ascends from left to right. For every unit increase in the x-axis, there is a proportional increase in the y-axis.
- Negative Slope: The line descends from left to right. For every unit increase in the x-axis, there is a corresponding decrease in the y-axis.
- Zero Slope: This is a horizontal line. The slope is zero because the y-coordinate remains constant regardless of the x-coordinate change.
- Undefined Slope: Vertical lines have an undefined slope since any change in y without a change in x leads to an infinite or undefined value.
Understand the Formula

The slope formula, often written as m = (y2 - y1) / (x2 - x1), is your compass for navigating through slope worksheets. Here’s how to effectively apply it:
- Choose Points Wisely: Pick two points from the graph or table of values that are easy to work with. If you’re dealing with a line segment, these are typically labeled endpoints.
- Calculate Differences: Subtract the y-coordinates first, then subtract the x-coordinates. This step gives you the rise and run respectively.
- Divide and Conquer: Divide the difference in y by the difference in x to get the slope (m).
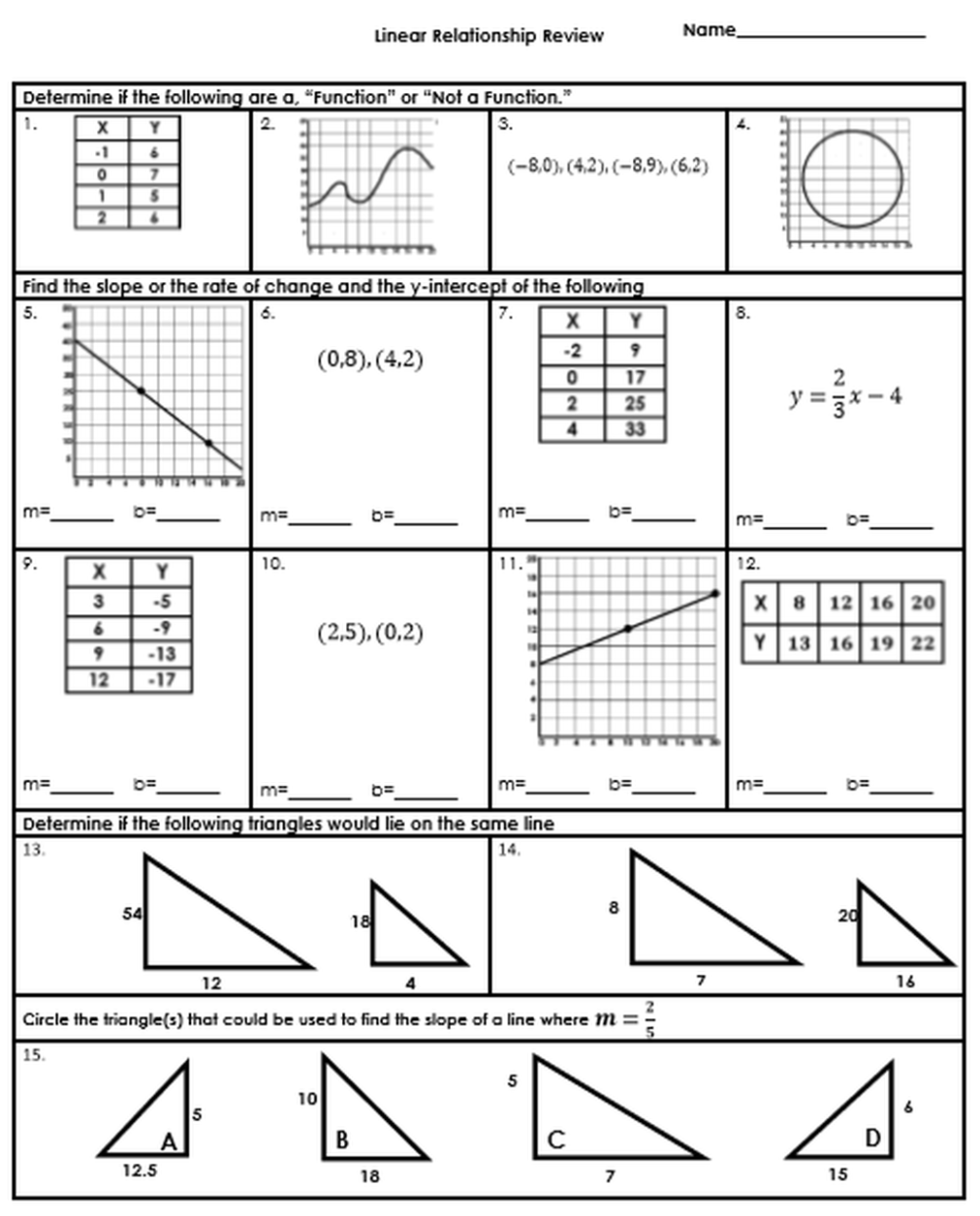
Visualize with Graphing


Graphing is an excellent way to visualize and understand slope. Here’s how:
- Set Up Your Graph: Use graph paper or digital graphing tools to plot your points accurately.
- Plot Points: After choosing two points, plot them on the graph.
- Draw the Line: Connect the points with a straight line. The angle and direction of this line will visually represent the slope:
- Positive slope lines will point upwards from left to right.
- Negative slope lines will point downwards from left to right.
- Horizontal lines will show zero slope.
- Vertical lines depict undefined slopes.
- Check Your Work: Use the graph to cross-check your slope calculations. The steeper the line, the larger the absolute value of the slope.
Work Through Slope Intercept Form

| Equation | Slope | Y-Intercept |
|---|---|---|
| y = mx + b | m | b |
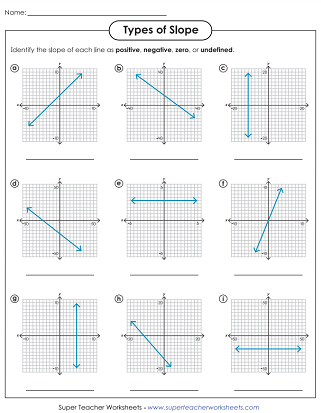
The slope-intercept form of a line’s equation, y = mx + b, is a fundamental tool for understanding slope and y-intercept directly from an equation:
- Identify the Slope (m): Directly read the coefficient of x. This is your slope.
- Locate the Y-Intercept (b): The constant term in the equation represents where the line crosses the y-axis.
- Practice Rearranging: Often, equations will not be in slope-intercept form. Practice rearranging linear equations to this form to quickly see the slope and y-intercept.
Utilize Slope Worksheets

Worksheets are like training manuals for mastering slopes:
- Look for Variety: Use worksheets that cover various slope scenarios, from basic to advanced. This includes finding slopes from given points, interpreting graphs, and applying the formula in real-life situations.
- Review Common Errors: Watch out for common mistakes like miscalculation of differences or confusing positive with negative slopes.
- Implement Timed Exercises: Practice under time constraints to simulate exam conditions, which can improve speed and accuracy.
- Create Your Own: Challenge yourself by making up your own slope problems. This not only reinforces your learning but also boosts problem-solving skills.
⚠️ Note: Always double-check your calculations to avoid sign errors and division by zero, which can lead to an undefined slope or incorrect solutions.
In sum, mastering slope worksheets requires a mix of understanding concepts, visualizing, practicing, and reviewing common mistakes. By identifying different slope types, understanding the slope formula, graphing, working with slope-intercept form, and utilizing varied worksheets, you'll climb the slope of difficulty with ease. Remember, every step you take in learning about slopes builds your foundation in algebra and beyond, preparing you for more complex mathematical explorations.
What if my slope calculation gives me a fraction?

+
When your slope calculation results in a fraction, it means the line is not as steep as when the slope is an integer. It’s still valid; just ensure you simplify the fraction if possible. For example, a slope of 2⁄4 can be simplified to 1⁄2.
How do I find the slope of a curve?

+
The slope of a curve at a specific point requires calculus to find the derivative of the function, which gives you the slope of the tangent line at that point. This topic goes beyond the basics of linear slopes discussed in this article.
What are some real-life applications of slope?

+
Slope has numerous real-life applications: architecture (roof pitch), road engineering (road grade), economics (demand curves), physics (ramp incline), and even sports analytics for understanding performance trends.