8 Ways to Master Reflections Worksheet 8th Grade

The reflections worksheet for 8th grade students often presents a challenging yet critical aspect of geometry. It's crucial for young mathematicians to not only understand the concept of reflections but also master the application through worksheets. Here, we'll explore eight effective strategies to help 8th graders excel in tackling reflections in their math assignments.
Understanding Reflections: The Basics

Before diving into the strategies, let’s ensure we’re on the same page regarding what a reflection is:
- A reflection is when an object is flipped over a line, known as the line of reflection.
- The original figure and its reflection are congruent, but they appear as mirror images of each other.
Reflections are commonly performed across:
- The x-axis
- The y-axis
- A diagonal line
Understanding the principles of reflections sets the stage for advanced learning and problem-solving.
1. Visualization Techniques

Visualize the Reflection: Encourage students to imagine the figure being folded along the line of reflection. This can help in:
- Understanding the direction of movement.
- Estimating the distance from the original shape to the reflected shape.
2. Practice with Tracing Paper

Physical manipulation can enhance learning:
- Trace the original shape on tracing paper, fold it over the line of reflection, and trace the reflected shape.
- This helps students grasp how the image aligns with the original after the reflection.
3. Use of Coordinate Geometry
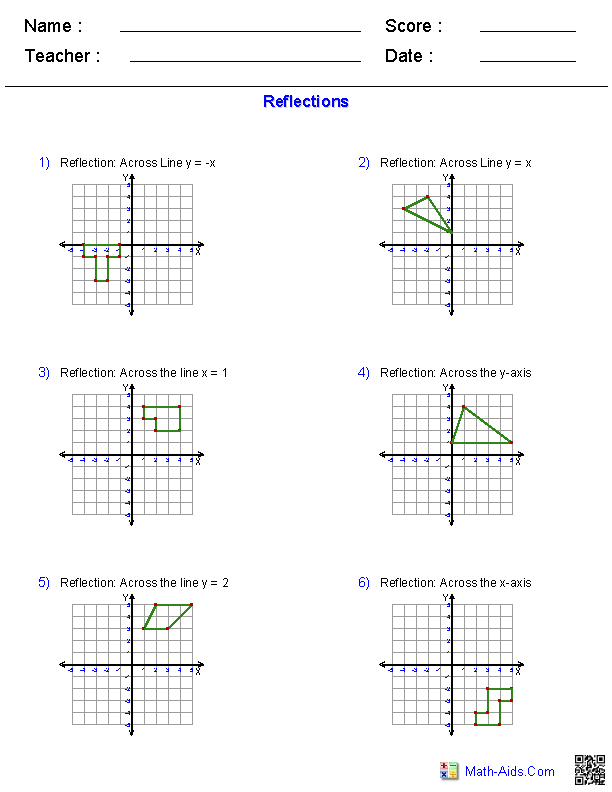
Coordinate geometry provides a precise method to perform reflections:
- Reflect over the x-axis: Change the sign of the y-coordinate.
- Reflect over the y-axis: Change the sign of the x-coordinate.
- Diagonal Reflections: Depending on the line of reflection, formulas are used to calculate the coordinates of the reflected point.
| Original Point | Reflection over X-axis | Reflection over Y-axis |
|---|---|---|
| (x, y) | (x, -y) | (-x, y) |

✏️ Note: Coordinate formulas for diagonal reflections can be complex. Encourage students to derive them with a teacher's guidance for better understanding.
4. Employing Graphing Tools
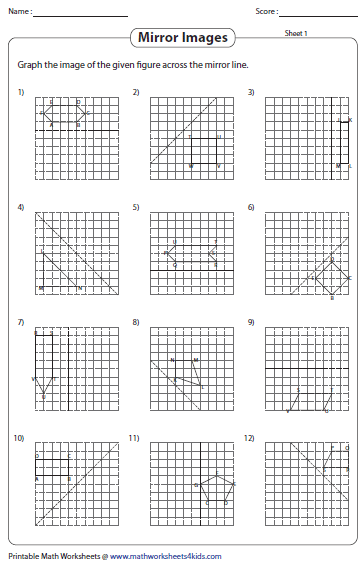
Modern technology can be an ally in teaching reflections:
- Use graphing calculators or software like GeoGebra to illustrate reflections instantly.
- Students can see how the original figure is manipulated, making the abstract concept more concrete.
5. Symmetry and Real-Life Applications

Linking reflections to real life:
- Symmetry: Show how reflections relate to symmetrical objects, from natural patterns to man-made structures.
- Real-Life Examples: Mirrors, water reflections, and artistic compositions provide everyday applications of reflections.
6. Step-by-Step Guided Practice
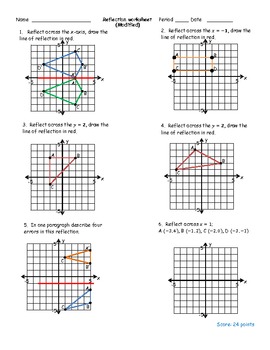
Detailed walkthroughs:
- Start with simple shapes like triangles or squares, gradually introducing complexity.
- Walk students through each step of reflecting a shape, asking them to verbalize the process.
7. Peer Learning and Teaching

Group work can be powerful:
- Allow students to explain reflections to each other, enhancing understanding through teaching.
- Pairing a struggling student with a peer who grasps the concept can be mutually beneficial.
8. Reflection Assessments and Feedback

Regular, constructive feedback:
- Give instant feedback on reflection exercises to reinforce learning.
- Use quizzes, worksheets, or even verbal quizzes to assess understanding and provide tailored feedback.
By employing these strategies, 8th graders can confidently tackle reflections worksheets. Keep in mind that mastering this skill involves not only understanding the concept but also practice, real-world application, and peer interaction. It's a journey from visualization to concrete mathematical problem-solving, enriched by every step along the way.
What is the purpose of reflections in geometry?

+
Reflections in geometry are used to understand symmetry, congruence, and transformation in space. They help in visualizing and understanding how objects or shapes change when flipped or mirrored.
How do you know if a shape has been reflected correctly?

+
A shape has been reflected correctly if:
- It maintains the same size (congruent).
- Its distance from the line of reflection is the same on both sides.
- Each point on the reflected shape is equidistant from its corresponding point on the original shape relative to the line of reflection.
What are some real-life examples of reflections?

+
Real-life reflections include:
- Mirror images
- Reflections in water (e.g., a pond or a lake)
- Architectural designs with symmetry, like buildings or bridges
- Symmetrical patterns in nature, like butterfly wings or the human face
💡 Note: Regular, structured practice will help students internalize these strategies effectively.



