Mastering Geometry with Reflections Worksheet Fun

Geometry has always been an essential part of mathematics, bridging the abstract to the practical world through shapes, angles, and transformations. Among these transformations, reflection stands out as both a fundamental concept and a fun tool for learning. In this comprehensive guide, we'll explore reflections in geometry through engaging worksheets and interactive activities that not only enhance understanding but also make learning an enjoyable experience.
Understanding Reflections in Geometry
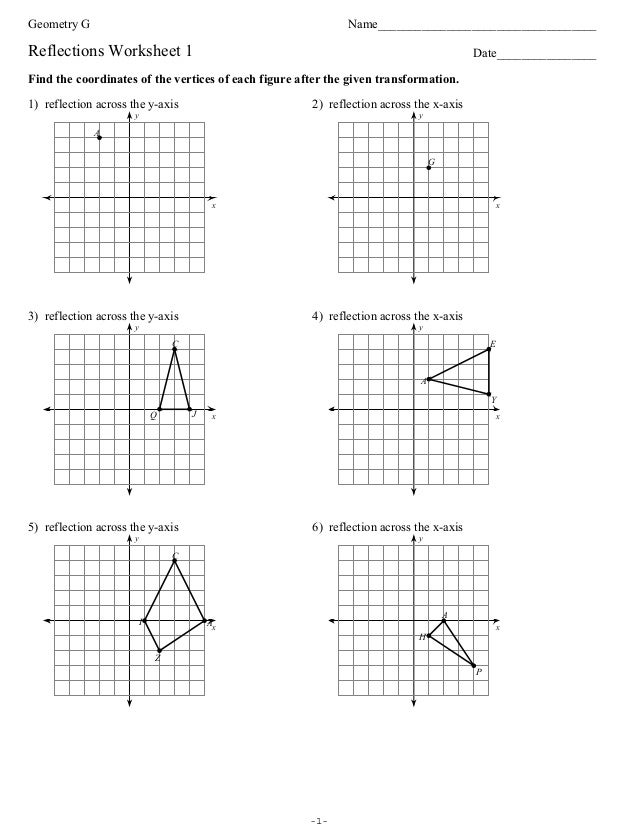
Reflection, also known as a flip or mirror transformation, involves creating a mirror image of a geometric shape across a line known as the line of reflection. Here’s how reflections work:
- Every point on one side of the line of reflection has a corresponding point an equal distance away on the other side.
- The shape of the figure remains identical, but its orientation changes.
- Distances, areas, and angles are all preserved in a reflection.
Reflecting a shape can be visualized by imagining that each point on the shape is being flipped over an imaginary line like a mirror. This transformation is used widely in art, design, and real-world scenarios like architecture or even in nature through the reflection of mountains in lakes.
Why Use Worksheets for Learning Reflections?

Worksheets provide a practical, hands-on approach to mastering geometry concepts:
- Reinforce Understanding: Worksheets allow students to practice the concept of reflections repeatedly, helping to solidify their understanding.
- Visual Learning: Geometry, being visual by nature, benefits from worksheets where learners can see and manipulate shapes.
- Interactive Learning: Worksheets can be designed to be interactive, where students might physically fold the paper to create reflections or use digital tools to simulate the process.
Worksheet Activities for Reflection Mastery

Simple Reflections
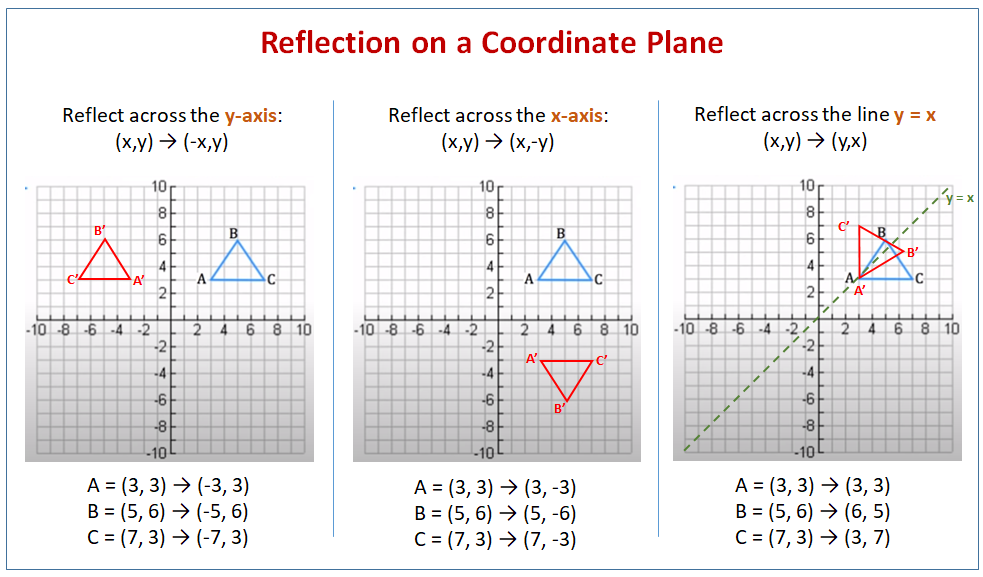
Start with basic shapes like squares, triangles, or letters of the alphabet. Provide students with:
- A worksheet with various shapes on one side of a dashed line.
- Ask them to draw the reflection of each shape on the other side of the line.
Here is a sample of how the worksheet might look:
_______
/ /|
/_______/ |
| | |
|_______|/
|
_______
/ /|
/_______/ |
| | |
|_______|/
|

📝 Note: Students can use a mirror or fold the worksheet to check their work.
Complex Reflections
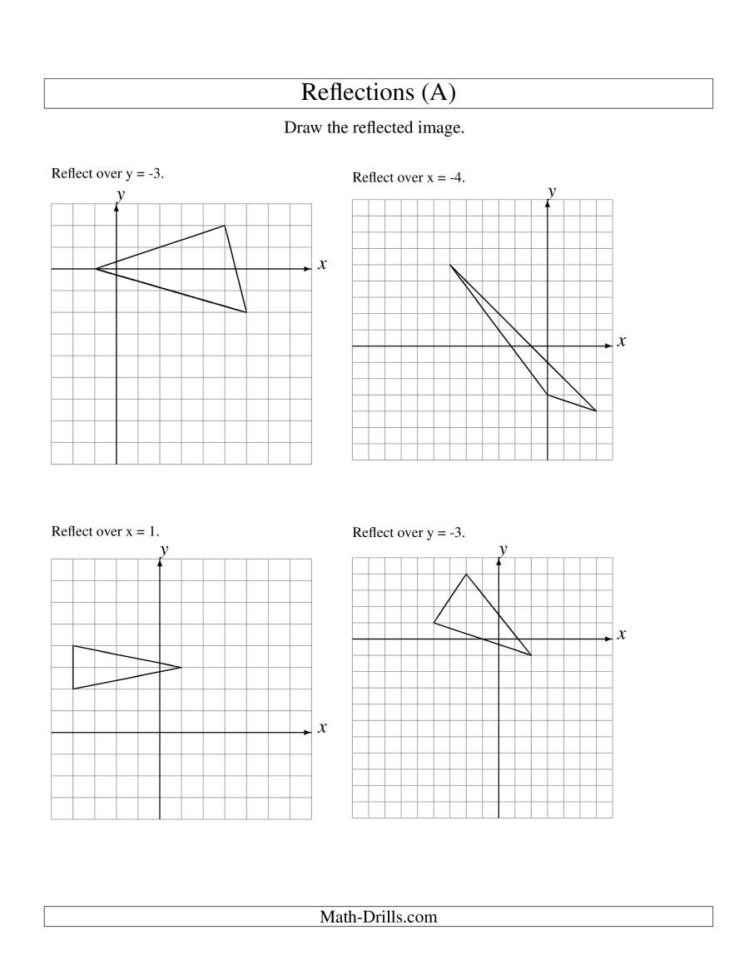
Move on to more complex shapes or scenarios:
- Reflect complex polygons or irregular shapes.
- Use grids to draw reflections of figures that intersect the line of reflection at various angles.
Reflection with Multiple Axes

This exercise introduces the concept of reflections across different axes:
- Provide a grid with a shape and multiple axes of reflection.
- Students reflect the shape across each axis one at a time and see how the final result changes.
Real-World Applications

To make learning more relatable:
- Have students reflect images of common objects like cars or buildings.
- Discuss how reflections appear in daily life (e.g., in mirrors, in photography).
Creating Interactive Reflection Worksheets

Here are some innovative ways to engage students:
- Use technology: Interactive online tools allow students to drag shapes across a line to see real-time reflections.
- Physical Engagement: Provide cut-outs or puzzles where students must match pieces with their reflections.
- Art and Design: Encourage students to create symmetrical art or logos by reflecting shapes in creative ways.
In sum, worksheets play a pivotal role in understanding reflections in geometry. They provide a structured yet creative space for students to explore, practice, and enjoy this fascinating aspect of math. Through a combination of traditional paper-based activities and modern digital tools, learners can develop a deep comprehension of how shapes relate in our mirrored world.
By integrating visual, interactive, and real-world applications into geometry education, students not only learn the mechanics of reflections but also develop a deeper appreciation for the beauty and precision of geometric transformations. Whether you're an educator looking to enhance your teaching methods or a student aiming to better understand geometry, reflections offer a versatile and engaging pathway to mastering this mathematical field.
What is a line of reflection?
+
A line of reflection is an imaginary line across which every point in a shape is flipped to create its mirror image. The original point and its reflected point are equidistant from this line.
How can you check if a reflection is correct?

+
To verify if a reflection is correct, you can use a mirror or physically fold the paper along the line of reflection. If the shapes align perfectly when viewed or aligned with the mirror or fold, the reflection is accurate.
Are reflections the same as rotations?

+
No, reflections and rotations are different transformations. While reflection flips an object over a line, rotation turns an object around a fixed point. Both transformations preserve shape and size but change orientation in different ways.
Can reflections change the size of shapes?

+
No, reflections preserve the size, shape, angles, and distances of the original figure. Only the orientation changes.
Why are reflections important in real life?

+
Reflections are used in many fields such as art, design, and architecture for symmetry and aesthetic purposes. They are also fundamental in optics, where the reflection of light off surfaces is studied. In everyday life, reflections appear in mirrors, water bodies, and even in our perception of spatial orientation.