Transform Geometry Skills: Reflection of Shapes Worksheet
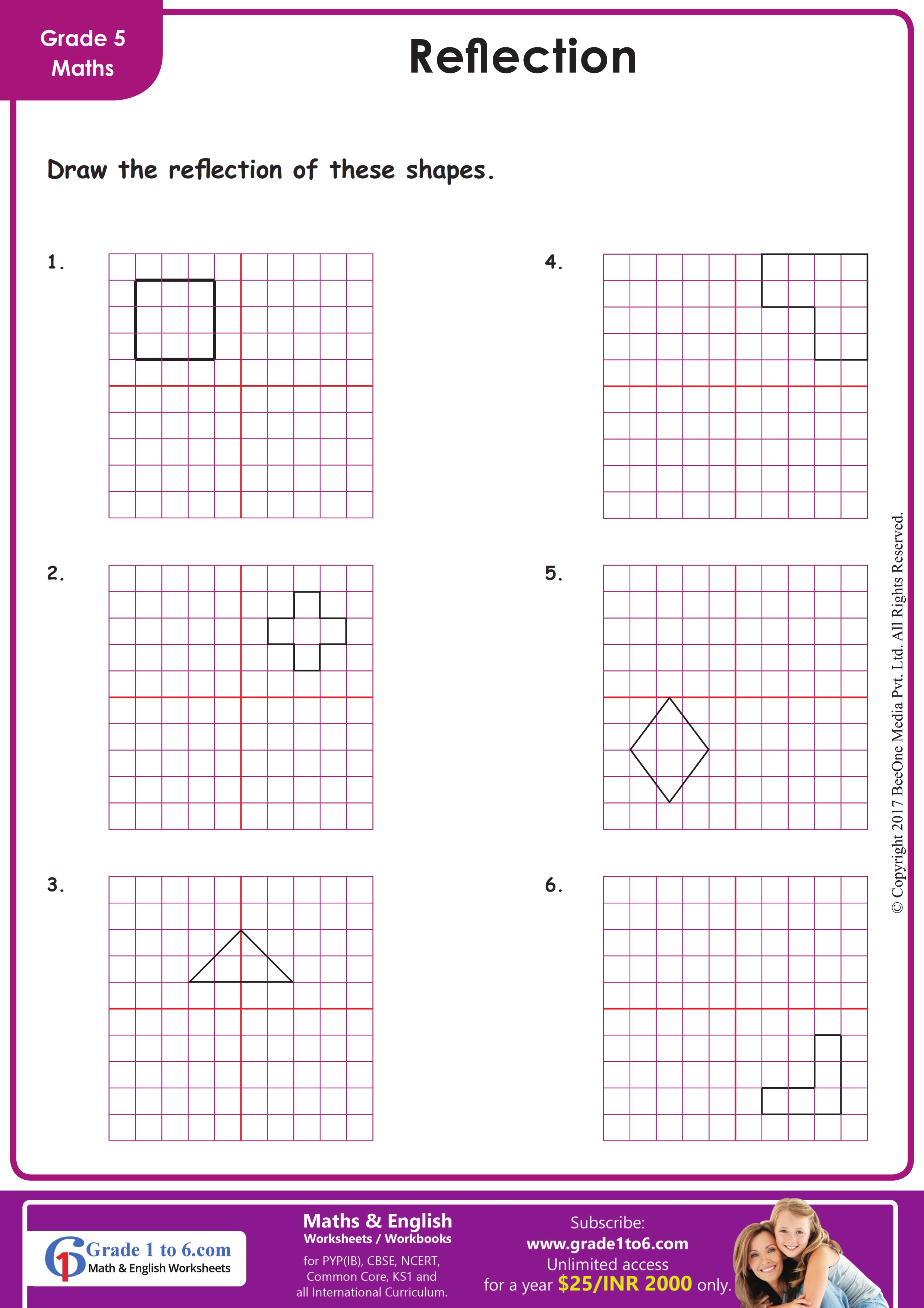
In the vast and intricate world of geometry, one of the fundamental transformations that students need to master is the reflection of shapes. Reflection, often referred to as a "flip," involves creating a mirror image of an object across a line known as the reflection axis or line of reflection. This transformation is essential in understanding symmetry and is a key aspect in various fields such as art, design, architecture, and of course, mathematics. In this comprehensive exploration, we will delve into what reflection of shapes entails, how to identify and perform this transformation, and how to practice it effectively through reflection worksheets.
Understanding Reflection in Geometry

Reflection, as a geometric transformation, preserves the size and shape of the object but changes its orientation. Here's a breakdown of what reflection involves:
- Line of Reflection: This is an imaginary line where the shape would fold to match its reflection.
- Mirror Symmetry: The reflected shape and the original shape are identical but opposite, like an object and its mirror image.
- Distance Preservation: Every point of the shape is equidistant from the line of reflection as its mirrored counterpart.
✍️ Note: The line of reflection does not have to be vertical, horizontal, or even straight; it can be any line in the plane.

Identifying Reflections

To identify if a shape has been reflected, consider the following steps:
- Check Orientation: The orientation of the shape changes; for example, if the top of the original shape was pointing upwards, the top of the reflected shape will point downwards.
- Distance Check: Each point of the shape should be the same distance from the line of reflection as its corresponding point after reflection.
- Matching Features: Features of the shape like corners or vertices should match their positions relative to the line of reflection.
How to Reflect Shapes

The process of reflecting a shape across a line involves several steps:
Step 1: Identify the Line of Reflection

Determine where the line of reflection will be. This could be a horizontal, vertical, or diagonal line, or even an edge of the shape itself.
Step 2: Choose Points

Choose key points of the shape, like vertices or midpoints. For example, if it’s a triangle, you might choose all three vertices.
Step 3: Measure the Distance

From each point, measure the perpendicular distance to the line of reflection.
Step 4: Plot Corresponding Points

Extend the perpendicular line past the reflection line by the same distance on the opposite side to plot the new point.
Step 5: Connect the Points

Connect the newly plotted points to form the reflected shape. Ensure the new shape mirrors the original in terms of size and form.
⚠️ Note: If the line of reflection passes through a point of the original shape, that point will remain fixed in the reflected shape.
Practical Examples of Reflection

To better illustrate reflection, here are a few scenarios:
- Mirror Image: Reflect a letter 'L' across a vertical line. The reflected 'L' would look like a 'J' with the top pointing down.
- Symmetrical Objects: Look at a butterfly or a face. These objects often exhibit reflective symmetry across a central line.
- Architectural Designs: Many buildings are designed with elements reflected across an axis, enhancing the visual appeal through symmetry.
Reflection Worksheets for Practice

Reflection worksheets are an excellent tool for practicing and understanding this transformation. Here's how you can make the most out of them:
- Tracing: Use graph paper or tracing paper to trace the original shape, then fold the paper along the line of reflection to see the reflection directly.
- Grid Reflection: Plot shapes on a grid and reflect them across grid lines, making sure to keep the shape's orientation and proportions correct.
- Freehand Reflection: After mastering grid-based reflections, try freehand reflections to hone your intuitive sense of symmetry.
Here is a simple table to understand the process of reflection better:
| Step | Description |
|---|---|
| 1. Identify | Determine the line of reflection. |
| 2. Measure | Measure the distance from each point to the line. |
| 3. Plot | Plot the corresponding point on the other side. |
| 4. Reflect | Connect these points to form the reflected shape. |

🎨 Note: Reflection worksheets often include activities like drawing symmetrical designs or patterns which can foster a deeper understanding and appreciation of symmetry in art and nature.
The Importance of Reflection in Real-World Scenarios

Understanding reflection goes beyond academic exercises; here are a few practical applications:
- Art and Design: Artists use reflection to create visually pleasing symmetrical images.
- Photography and Cinematography: Reflections can be used creatively for storytelling or to add depth to images.
- Geophysics: Seismic reflection is used to explore subsurface layers of the earth.
- Computer Graphics: Reflections are integral to realistic rendering and virtual reality.
In conclusion, mastering the reflection of shapes in geometry not only enhances one's understanding of symmetry but also lays a foundation for various applications in real life. Through practice with reflection worksheets, one can improve their spatial reasoning, intuitive grasp of geometry, and even their artistic abilities. The process, while straightforward, fosters critical thinking and precision, essential skills in many disciplines.
What is the difference between reflection and rotation?

+
Reflection and rotation are both geometric transformations, but they differ fundamentally. Reflection creates a mirror image of an object across a line, maintaining its size but changing its orientation. Rotation, on the other hand, involves turning an object around a point or axis, keeping its shape and size but altering its direction or facing. Reflection flips, while rotation turns.
Can any shape be reflected?

+
Yes, any two-dimensional shape can be reflected across a line. However, complex shapes might require more steps or calculations to reflect accurately. The key is to ensure every point on the original shape has a corresponding mirrored point on the reflected shape.
How can reflection worksheets help in learning?

+
Reflection worksheets provide a practical, visual, and hands-on approach to understanding symmetry and transformation in geometry. They encourage active learning, help develop spatial awareness, and can be tailored to different skill levels, making them an effective tool in educational settings.