5 Tips for Mastering Reference Angles Quickly

Mastering reference angles in trigonometry can seem like a daunting task at first glance. However, with the right approach, you can quickly gain proficiency in understanding and using reference angles to solve trigonometric problems. In this blog, we delve into five practical tips that will help you master reference angles swiftly and effectively.
Understand the Concept of Reference Angles

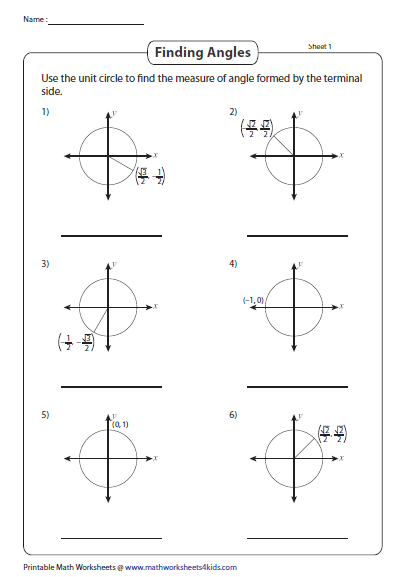
Reference angles are an essential part of trigonometry, particularly when working with angles outside the standard 0-90 degrees range. Here are the basic steps to find the reference angle:
- Identify the Quadrant: Determine which quadrant the angle falls into. Here’s how:
- First Quadrant: 0° to 90°
- Second Quadrant: 90° to 180°
- Third Quadrant: 180° to 270°
- Fourth Quadrant: 270° to 360°
- Find the Reference Angle:
- For angles in the First Quadrant, the reference angle is the angle itself.
- In the Second Quadrant, subtract the angle from 180°.
- In the Third Quadrant, subtract 180° from the angle.
- For angles in the Fourth Quadrant, subtract the angle from 360°.
📝 Note: Remember, the reference angle is always between 0° and 90°.
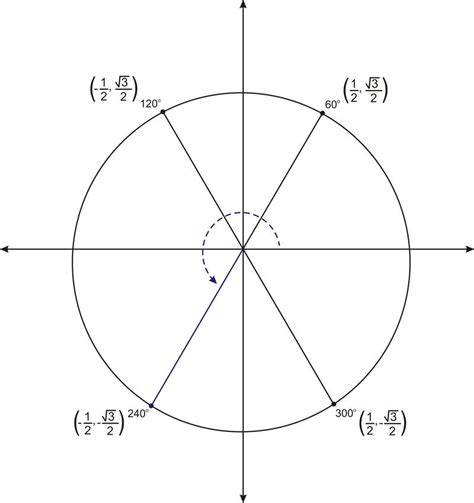
Utilize Unit Circle Relationships

Visualizing the unit circle can make finding reference angles intuitive:
- Angles in the First Quadrant are their own reference angles.
- Second Quadrant angles' reference angles are reflected over the y-axis.
- In the Third Quadrant, reference angles are found by subtracting from 180° or by reflection over the x-axis.
- Fourth Quadrant angles are the angle's distance from 360°.
🔗 Note: Memorizing common angles on the unit circle helps in quick reference angle calculation.
Practice with Trigonometric Functions
Using trigonometric functions like sin, cos, and tan can reinforce your understanding:
- sin(θ) = sin(Reference Angle) for angles in the First and Second Quadrants.
- cos(θ) = ±cos(Reference Angle) for all quadrants, with positive in First and Fourth, negative in Second and Third.
- tan(θ) = ±tan(Reference Angle), where the sign depends on the quadrant.
Here is a table to illustrate how trigonometric functions relate to reference angles:
| Quadrant | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| First | + | + | + |
| Second | + | - | - |
| Third | - | - | + |
| Fourth | - | + | - |

Use Symmetry to Your Advantage

Trigonometric functions often exhibit symmetry, which can be used to simplify calculations:
- cosine is even, meaning cos(-θ) = cos(θ).
- sine is odd, so sin(-θ) = -sin(θ).
- Angles with the same reference angle but in different quadrants often yield related results.
By recognizing these patterns, you can quickly determine the reference angle without tedious calculations.
Solve Real-world Applications
Applying reference angles to real-world scenarios can solidify your understanding:
- Projectile Motion: For calculating maximum height or range, understanding reference angles helps in determining the angle of projection relative to the horizontal.
- Engineering: When dealing with forces or vectors, reference angles are crucial for resolving components.
- Navigation: Bearing angles can be converted into reference angles for mathematical analysis.
⚙️ Note: Reference angles are not just a mathematical abstraction; they have practical applications in various fields.
In summary, mastering reference angles involves understanding their fundamental concept, utilizing visual aids like the unit circle, practicing with trigonometric functions, exploiting symmetry, and applying knowledge to real-world scenarios. By following these five tips, you'll not only grasp reference angles more quickly but also enhance your overall proficiency in trigonometry. Keep in mind that consistent practice and application are key to mastering any mathematical concept.
What are the benefits of understanding reference angles?

+
Understanding reference angles simplifies trigonometric calculations, reduces error in problem-solving, and aids in visualizing angular relationships, which is beneficial for both academic and practical applications in various fields like engineering and physics.
Can reference angles be negative?

+
Reference angles themselves are always positive, as they represent the smallest angle the terminal side of an angle makes with the x-axis, which is inherently positive.
How does knowing reference angles help with solving trigonometric identities?
+
Knowing reference angles helps in simplifying complex trigonometric identities. It allows you to convert angles from one quadrant to another, making the process of identity verification more straightforward, especially for verifying co-function identities.
Why are reference angles important in real-world scenarios?

+
Reference angles are crucial for applications involving angle measurement, navigation, design, and analysis in fields like architecture, engineering, and navigation. They provide a standardized way to understand angles beyond the basic 0-90° range.
Related Terms:
- Reference angle worksheet pdf
- Reference angle worksheet with answers
- Coterminal angles worksheet with answers