5 Ways to Master Reducing Fractions Easily

Understanding how to reduce fractions is an essential math skill that not only simplifies arithmetic but also deepens one's understanding of numbers and their relationships. Let's explore five effective methods to master reducing fractions, ensuring you're equipped with the knowledge to handle these mathematical tasks with ease.
1. Using the Greatest Common Divisor (GCD)
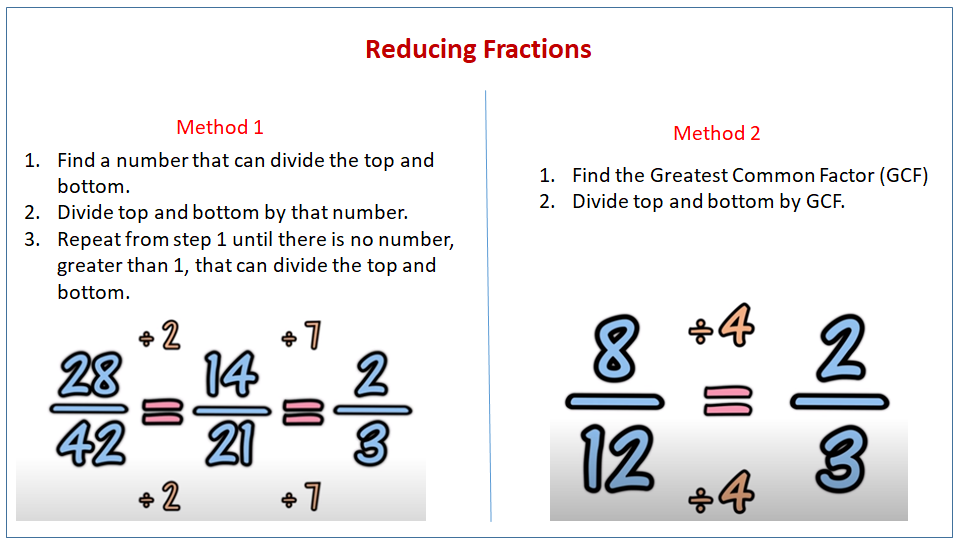

The most foundational way to reduce fractions is by finding the greatest common divisor (GCD) of the numerator and the denominator. Here's how to do it:
- List the factors: Write down all the factors of both numbers.
- Identify the GCD: Find the largest number that both lists share.
- Divide: Use the GCD to divide both the numerator and the denominator.
Consider the fraction 36/48:
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- GCD: 4
- Reduced Fraction: 36 ÷ 4 = 9, 48 ÷ 4 = 12. The reduced fraction is 9/12.
🔍 Note: If the GCD is 1, the fraction is already in its simplest form.
2. Cancel Out Common Factors


Another approach is to cancel out common factors step-by-step:
- Prime Factorization: Break down both the numerator and denominator into their prime factors.
- Cancel: Cross out any common prime factors in the numerator and the denominator.
- Multiply: Multiply the remaining factors to get the reduced fraction.
Using the same fraction 36/48:
- Prime factorization of 36: 2 \times 2 \times 3 \times 3 = 36
- Prime factorization of 48: 2 \times 2 \times 2 \times 2 \times 3 = 48
- Canceling out: 2 \times 2 \times \cancel{3} \times 3 / (2 \times 2 \times 2 \times \cancel{3})
- Reduced Fraction: 3 / 4 = 3/4
📝 Note: This method becomes especially efficient with larger numbers, where factoring directly into primes can be less intimidating.
3. Using the Euclidean Algorithm


This sophisticated yet simple method uses division to find the GCD:
- Divide: Divide the larger number by the smaller one to get the quotient and the remainder.
- Substitute: Replace the larger number with the smaller, and the smaller with the remainder.
- Repeat: Continue until the remainder is zero. The divisor at that point is the GCD.
Using 36/48:
- 48 ÷ 36 = 1, Remainder: 12
- 36 ÷ 12 = 3, Remainder: 0
- GCD: 12
- Reduced Fraction: 36 ÷ 12 = 3, 48 ÷ 12 = 4. The reduced fraction is 3/4.
4. Using a Calculator or Online Tools


In our digital age, you can also use calculators or online tools to reduce fractions:
- Enter the Fraction: Type in the fraction you want to simplify.
- Calculate: Use the simplify or reduce function.
- Read the Result: The tool will provide the reduced form of the fraction.
Here's a basic example for the fraction 36/48:
| Original Fraction | Reduced Fraction |
|---|---|
| 36/48 | 3/4 |

🔧 Note: Using tools can save time but does not offer the learning experience of manually reducing fractions.
5. Continuous Division by Small Primes

A method that works well for smaller fractions or when teaching others involves dividing both the numerator and the denominator by the smallest primes (2, 3, 5, etc.):
- Divide by 2: Continue until both numbers are not divisible by 2.
- Move to 3: If possible, divide by 3 repeatedly.
- Continue: Proceed with other small primes until no further reduction is possible.
Let's reduce 36/48:
- Divide by 2: 18/24
- Divide by 2: 9/12
- Divide by 3: 3/4
This method ensures you find the lowest terms of the fraction by systematically eliminating common factors.
Mastering these five ways to reduce fractions will not only enhance your problem-solving skills but also help you understand the mathematical relationships at play. Each method offers a unique approach, from foundational techniques like using the GCD or Euclidean Algorithm to more practical steps like using technology or dividing by small primes. By practicing these methods, you'll develop a deeper appreciation for the elegance and efficiency of fraction simplification.
What does it mean to reduce a fraction?

+
Reducing a fraction means finding the simplest form of that fraction where the numerator and denominator share no common factor other than 1. This process simplifies the fraction, making it easier to work with mathematically.
Why is it important to reduce fractions?

+
Reducing fractions simplifies arithmetic operations, which is crucial in understanding concepts like equivalent fractions, comparing fractions, and performing calculations efficiently. It also aids in understanding the proportional relationships between numbers.
Can a reduced fraction ever have a larger numerator or denominator than the original?

+
No. When you reduce a fraction, both the numerator and the denominator will always be less than or equal to the original values, assuming the fraction is not already in its simplest form.
Are there fractions that can’t be reduced?

+
A fraction cannot be reduced if the numerator and the denominator are coprime (they share no common factors other than 1). For example, 7⁄8 cannot be further reduced.
How can I check if my reduced fraction is correct?

+
To verify the reduced fraction, you can multiply both the numerator and the denominator by the GCD you found to ensure you return to the original fraction. Alternatively, use a calculator or online tools for cross-verification.