Simplify Fractions Easily: Lower Terms Worksheet Guide

Understanding how to simplify fractions is a crucial skill in math, with practical applications ranging from cooking and carpentry to engineering and daily decision-making. But while the concept might be simple, simplifying fractions often becomes a point of confusion for many. In this comprehensive guide, we will delve into the art of simplifying fractions, focusing particularly on the Lower Terms Worksheet approach. Here, you'll learn effective techniques for reducing fractions to their simplest form, ensuring clarity in all your math work. By mastering these techniques, you'll enhance your number sense, improve your algebraic skills, and gain a more intuitive grasp of proportions and ratios.
Understanding Fractions and Simplification

Before we dive into the specifics of the Lower Terms Worksheet, let's briefly revisit the basics of fractions. A fraction represents a part of a whole, written as a/b, where a (the numerator) signifies the number of parts we have, and b (the denominator) denotes how many parts make up the whole. Simplifying or reducing a fraction means finding an equivalent fraction where the numerator and denominator share no common factors other than one, essentially stripping away unnecessary complexity.
Why Simplify Fractions?

- Clarity: Simplified fractions are easier to read and understand, making them preferable in everyday use.
- Efficiency: Working with smaller numbers can be more straightforward and less prone to errors.
- Comparison: It's easier to compare fractions when they are in their simplest form.
The Lower Terms Worksheet Technique

The Lower Terms Worksheet method is a structured approach to simplifying fractions. Here’s how it works:
Step 1: Identify Common Factors

Begin by finding the common factors of the numerator and denominator. This can be done manually or by using tools like the Euclidean algorithm, but for simplicity, we'll focus on the worksheet method:
- List the factors of the numerator and denominator.
- Identify the highest number that both lists share.
Step 2: Divide by the Greatest Common Divisor (GCD)
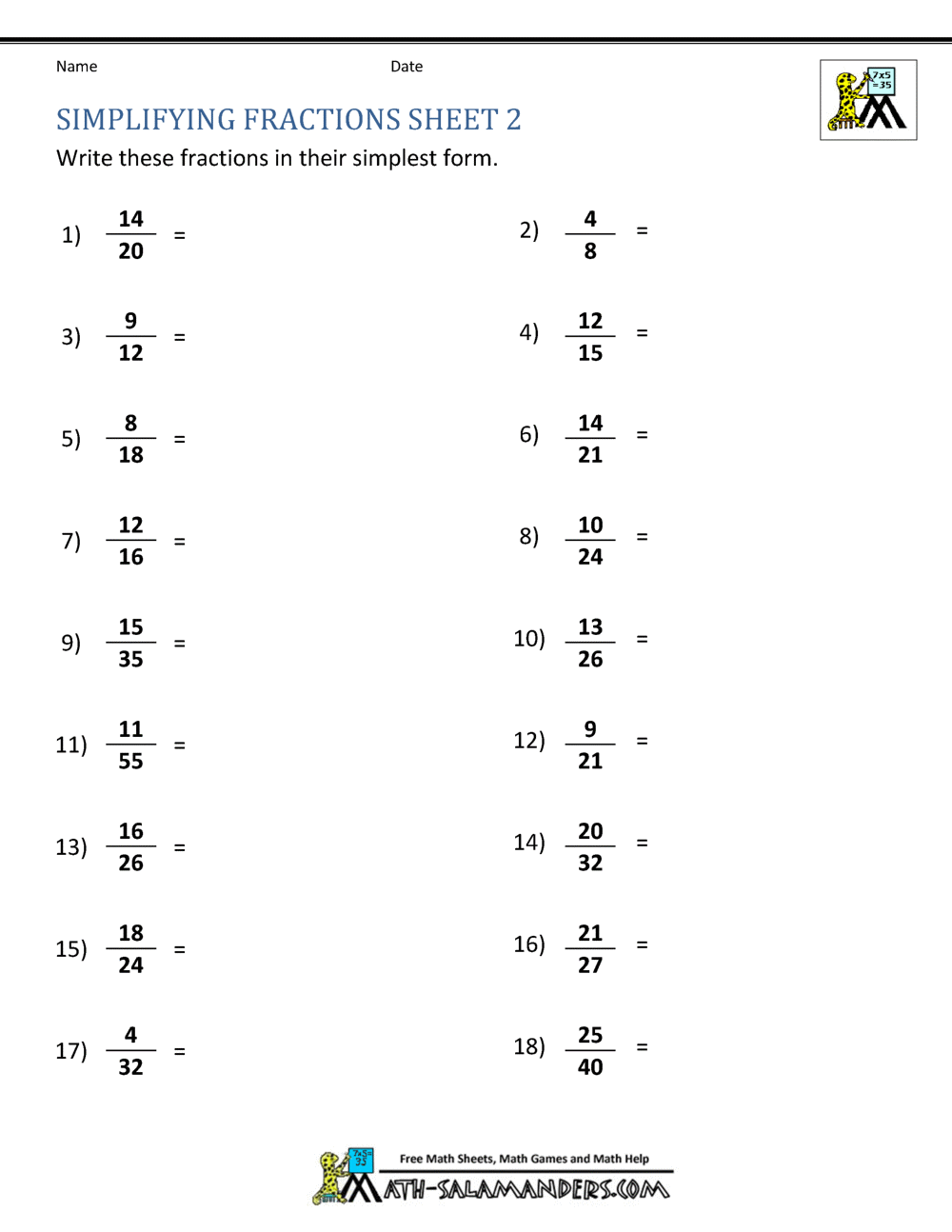
Divide both the numerator and the denominator by their greatest common divisor (GCD):
| Numerator | Denominator | Divided by |
|---|---|---|
| Original | Original | GCD |
| Result | Result | N/A |

💡 Note: In the case of mixed numbers, convert them to improper fractions first before simplifying.
Step 3: Validate the Simplification

After performing the division, check that:
- The new fraction is smaller than the original.
- The new numerator and denominator share no common factors other than one.
- Ensure the sign of the fraction remains consistent.
Practical Example
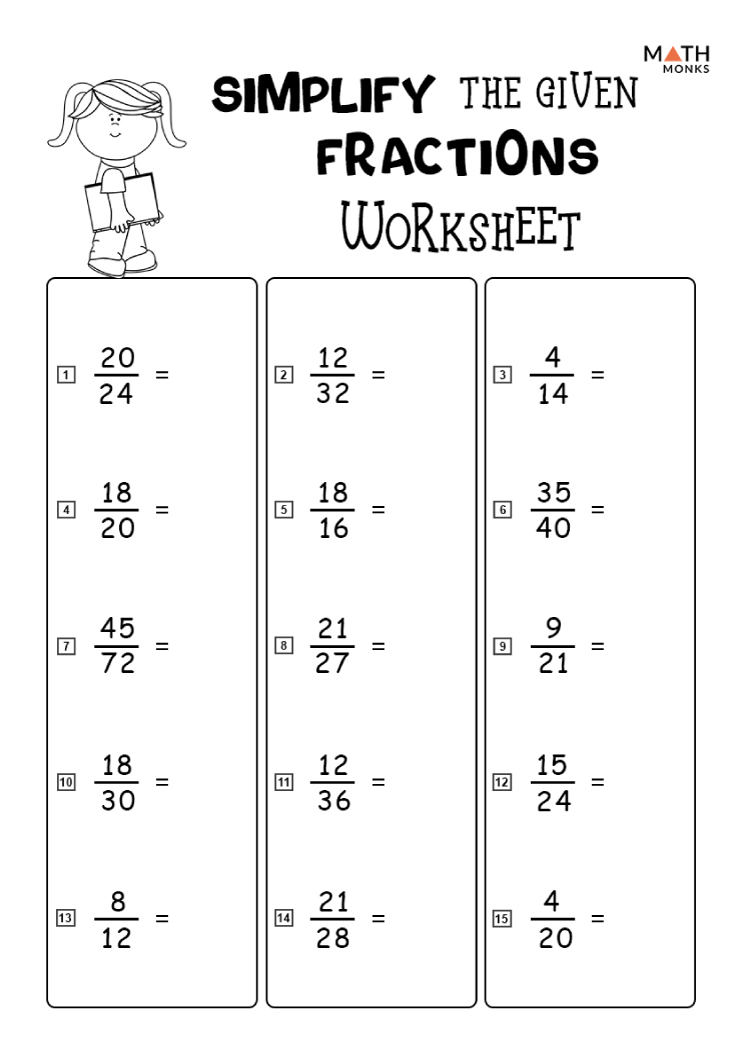
Let's simplify the fraction 48/64 using the Lower Terms Worksheet approach:
Step 1: Identify Common Factors
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
The factors of 64 are: 1, 2, 4, 8, 16, 32, 64.
The GCD is 16.
Step 2: Divide by the GCD
Divide both numerator and denominator by 16:
| Numerator | Denominator | Divided by |
|---|---|---|
| 48 | 64 | 16 |
| 3 | 4 | N/A |
So, 48/64 simplifies to 3/4.
Handling Improper Fractions

When working with improper fractions, it's often necessary to convert them back to mixed numbers if the context requires it. Here's how:
- Perform the simplification as usual.
- If the fraction is still improper, divide the numerator by the denominator to find the whole number part.
- Place the remainder over the denominator as the fractional part.
Example: 12/8 simplifies to 3/2, which converts to 1 1/2.
Conclusion
In this guide, we've explored a practical, worksheet-based approach to simplifying fractions, demonstrating how the Lower Terms Worksheet technique can make a seemingly complex task straightforward and systematic. By identifying the greatest common divisor of the numerator and denominator and dividing both by this number, we reduce fractions to their simplest form, enhancing clarity, efficiency, and ease of comparison in all mathematical operations involving fractions. Regular practice with this method will strengthen your ability to quickly reduce fractions and increase your confidence in handling fractions in a variety of real-world applications.
What if my fraction has large numbers?

+
For large numbers, using prime factorization or online tools to find the GCD can make the process more manageable. Remember, the goal is to find the largest number that divides both numerator and denominator without leaving a remainder.
Can I simplify negative fractions?

+
Yes, you can simplify negative fractions by focusing on the absolute values of the numerator and denominator. The sign of the fraction remains the same after simplification.
Why is it important to simplify fractions?

+
Simplifying fractions makes them easier to work with, especially in calculations, comparisons, and when presenting data in a clear and understandable format. It also reduces the chance of errors when dealing with fractions in various mathematical operations.