Rectangular Prism Surface Area Fun Worksheet

Exploring Rectangular Prisms

Let's embark on a fun and educational journey through the world of rectangular prisms. These fascinating shapes are not just basic building blocks of geometry but are integral in understanding three-dimensional space. Whether you're teaching, learning, or simply curious about geometry, understanding how to calculate the surface area of a rectangular prism can be both practical and fun.
Understanding Surface Area

The surface area of a rectangular prism (or cuboid) is the sum of the areas of all its faces. Here's a straightforward breakdown:
- There are six faces in a rectangular prism, but we essentially calculate the areas of three pairs of identical sides:
- Two rectangles with dimensions L x W
- Two rectangles with dimensions L x H
- Two rectangles with dimensions W x H
Thus, the formula for surface area of a rectangular prism is:
Surface Area = 2(LW + LH + WH)
where:- L is the length
- W is the width
- H is the height
⚠️ Note: Don't forget to double each face's area since there are two of each!
Interactive Worksheet: Fun with Surface Area

Here's an interactive worksheet designed to not only teach but also entertain:
Activity 1: Label and Find
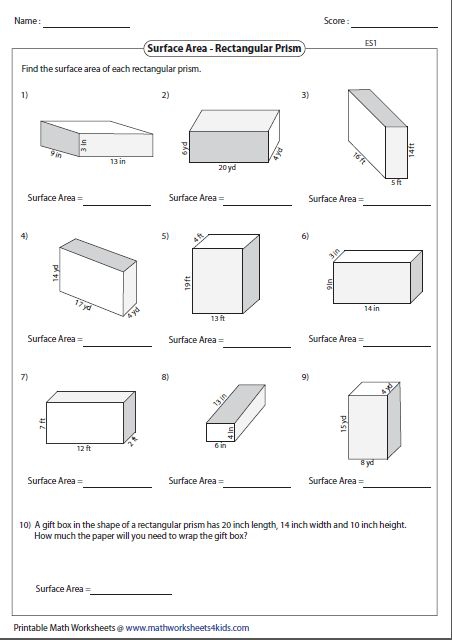
| Dimension | Value (in cm) |
|---|---|
| Length (L) | Enter length here |
| Width (W) | Enter width here |
| Height (H) | Enter height here |
| Surface Area | Enter calculation result here |

Enter the dimensions of a rectangular prism in the table above, calculate the surface area, and see how your results compare with your peers or a pre-set answer!
Activity 2: Real-Life Application
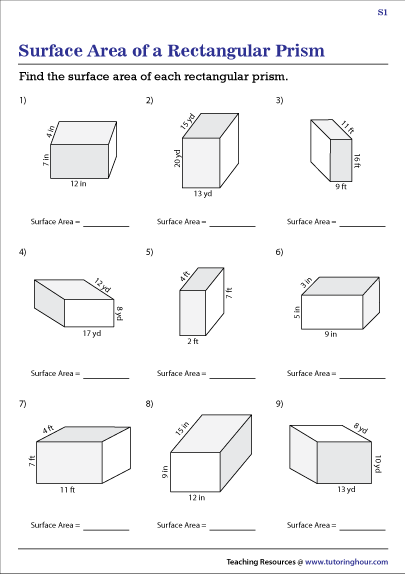
- Consider a box that you might use for packaging or storage:
- What if the box has a length of 12 cm, a width of 8 cm, and a height of 6 cm?
- Calculate the surface area using the formula.
- Now imagine you're wrapping this box. How much wrapping paper would you need? Here's a hint: you need to cover all the faces, but you might leave a bit of overlap for taping or folding.
Enhancing Your Learning Experience

Geometry isn’t just about numbers and equations; it’s about visualizing and understanding shapes in our three-dimensional world. Here are some tips to make your learning process engaging:
- Use physical objects like books or boxes to visualize prisms.
- Practice with various shapes and sizes to understand how dimensions affect the surface area.
- Play math games that involve calculating areas or volumes, which can make learning fun and competitive.
Revisiting Key Points

The journey through calculating the surface area of rectangular prisms has shown us how to:
- Use the formula 2(LW + LH + WH) effectively.
- Apply geometry in real-life situations like packaging or design.
- Understand how each dimension contributes to the overall size and area of a 3D object.
Why do we double the area of each face when calculating the surface area?
+
Because a rectangular prism has two faces of each type, and we need to account for the entire external area.
Can the surface area of a rectangular prism ever be zero?

+
No, because all dimensions must be positive, resulting in positive surface areas for all faces.
How does the surface area change if one dimension is zero?

+
If any dimension (L, W, or H) is zero, the shape effectively becomes a 2D plane, and the surface area calculation simplifies significantly.
Is there any practical application of knowing the surface area?

+
Yes, it’s used in manufacturing, packaging, construction, and even art to determine how much material is needed to cover or construct objects.
What’s the difference between surface area and volume in prisms?

+
Volume tells you how much space a shape occupies, while surface area measures how much outside surface the shape has.
Related Terms:
- Triangular prism surface area Worksheet