Real Number System Worksheet Answer Key: 5 Quick Checks
Understanding the Real Number System

The real number system encompasses various types of numbers that together form a complete system used in mathematics, science, and everyday life. These include:
- Natural Numbers: Counting numbers from 1 to infinity.
- Whole Numbers: Natural numbers including zero.
- Integers: Both positive and negative whole numbers, plus zero.
- Rational Numbers: Numbers that can be expressed as a fraction or ratio, where the numerator and denominator are integers, and the denominator is not zero.
- Irrational Numbers: Numbers that cannot be expressed as a simple fraction; their decimal expansions are non-repeating and non-terminating.
- Real Numbers: All rational and irrational numbers combined.
Classify the Numbers

Understanding how to classify numbers within the real number system is crucial for various mathematical operations:
- Whole Number? A number is considered a whole number if it's a positive integer or zero.
- Integer? An integer can be positive, negative, or zero but must not have a decimal or fraction.
- Rational Number? If it can be written as a fraction of two integers, where the denominator is not zero.
- Irrational Number? These numbers cannot be expressed as a fraction or ratio of integers and have infinite non-repeating decimal expansions.
- Real Number? All numbers that aren't imaginary are real numbers, encompassing all the categories above.
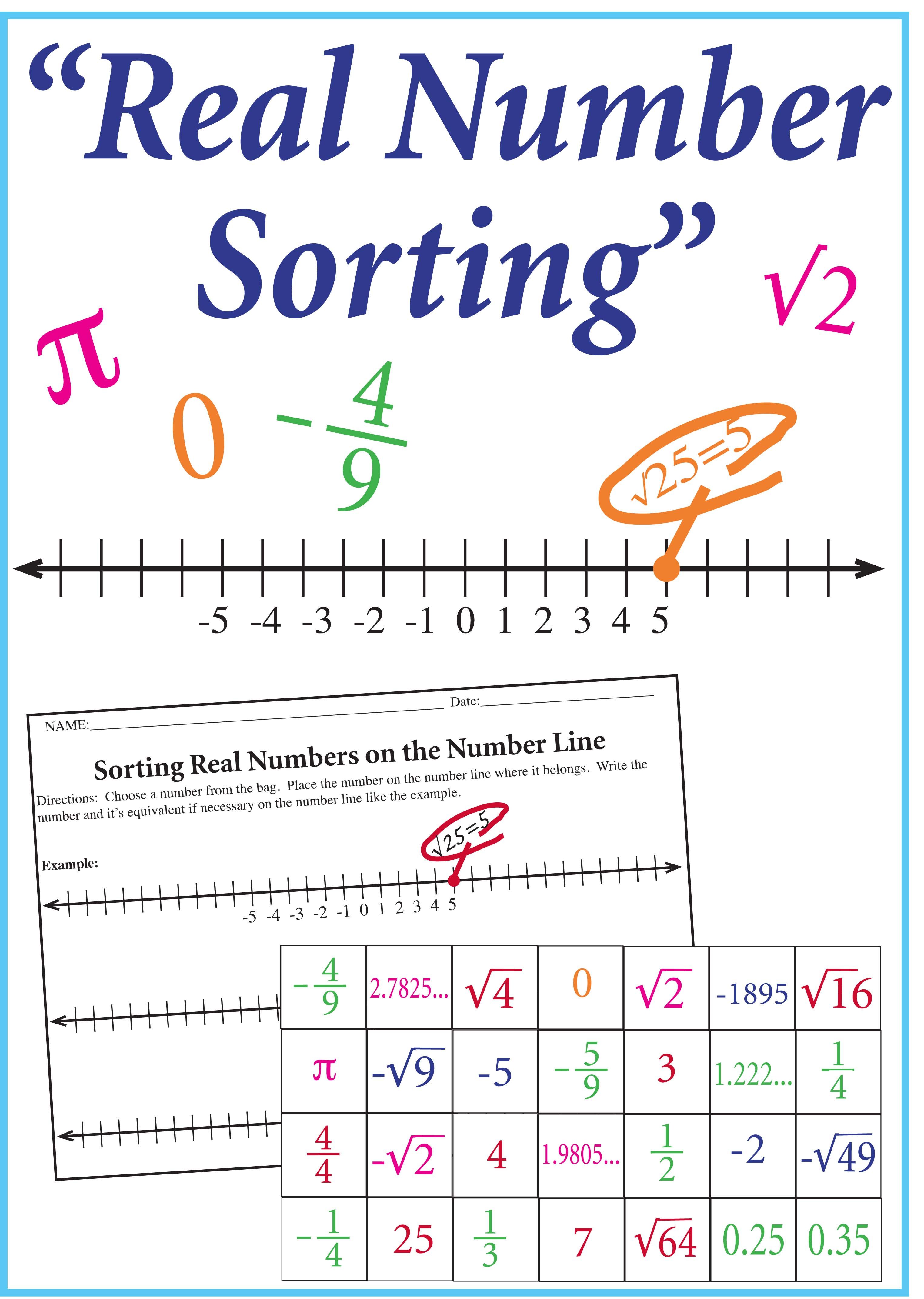
✏️ Note: When dealing with square roots, an integer is rational if it's a perfect square like √4, otherwise, it's irrational like √2.
Operations with Real Numbers

Here’s how to perform basic operations on real numbers:
- Addition and Subtraction: Combine or subtract like terms (rational or irrational).
- Multiplication: Rational times rational is always rational; however, irrational times irrational might yield rational or irrational.
- Division: When dividing, rational by rational gives rational; irrational by rational or vice versa gives irrational; irrational divided by irrational can go either way.
- Powers and Roots: Powers can make rational numbers irrational or vice versa, and taking the square root of a perfect square results in a rational number, otherwise, it's often irrational.
Place on the Number Line

To place numbers on the number line:
- Identify whether the number is positive, negative, or zero.
- For integers and whole numbers, marking is straightforward.
- For fractions, convert to a decimal and approximate the location.
- Plotting irrational numbers requires estimation or simplification to an approximate location.
Real Number Properties

The following are some key properties of real numbers:
- Closure: Addition, subtraction, multiplication, and division of two real numbers yield another real number (with the exception of division by zero).
- Commutative: Numbers can swap places without changing the result (a+b = b+a, a*b = b*a).
- Associative: Operations grouped in any way will still yield the same result [(a+b)+c = a+(b+c)].
- Distributive: Multiplication distributes over addition [a(b+c) = ab+ac].
- Identity Elements: There exists an identity for addition (0) and multiplication (1).
- Inverse Elements: Each real number has an additive and multiplicative inverse except for zero, which has no multiplicative inverse.
- Denseness: Between any two real numbers, there are infinitely many other real numbers.
In summary, understanding the real number system, classifying numbers, performing operations, placing numbers on a number line, and recognizing their properties are foundational for mathematical proficiency. This knowledge enables one to solve complex problems, understand advanced topics in algebra, and grasp the behavior of real numbers in various contexts.
What are the differences between rational and irrational numbers?

+
Rational numbers can be expressed as the ratio of two integers (e.g., 1⁄2, 0.5), while irrational numbers cannot be expressed this way and have non-repeating, non-terminating decimal expansions (e.g., π, √2).
How do you classify square roots as rational or irrational?

+
A square root of an integer is rational if it’s a perfect square (e.g., √4 = 2). If not, the result is irrational (e.g., √2 is irrational).
What’s the importance of knowing the real number properties?

+
Understanding these properties aids in simplifying calculations, proving mathematical statements, and navigating through algebraic operations smoothly.
Are there any real numbers that are neither rational nor irrational?

+
No, all real numbers are either rational or irrational. They cover all possible numbers from negative infinity to positive infinity, including zero.
How does the denseness property affect the number line?

+
Denseness means that between any two real numbers, there are infinitely many other real numbers. This property ensures that we can always find a number between any two chosen numbers, making the real number line continuous.