5 Fun Ways to Identify Rational vs. Irrational Numbers

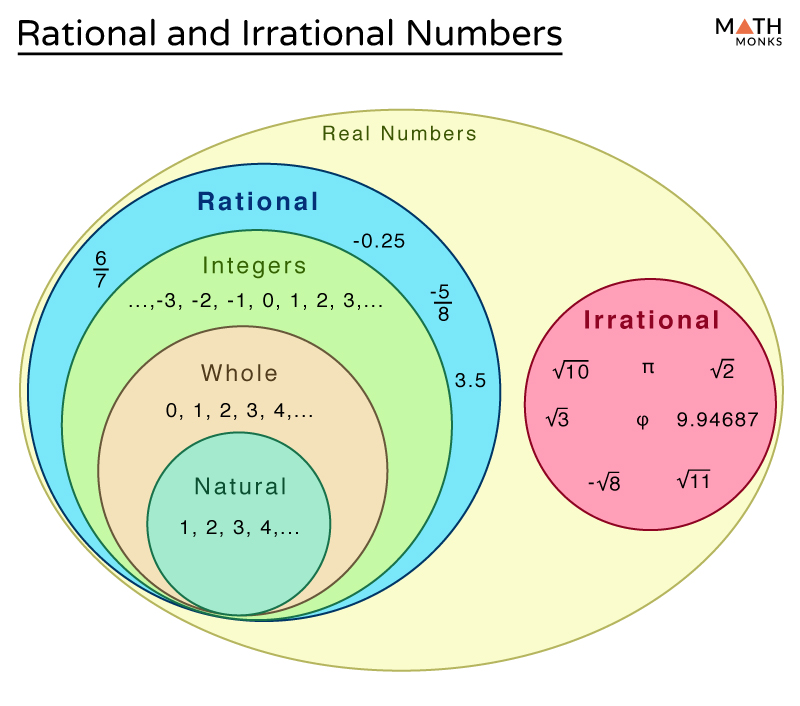
The Basics of Rational Numbers

To kick off our journey into the world of mathematics, let's first delve into the basics of rational numbers. A rational number is any number that can be expressed as the ratio of two integers, where the denominator is not zero. In simpler terms, rational numbers are those numbers that can be written in the form \frac{a}{b}, where a and b are integers and b \neq 0.
Here are some key characteristics of rational numbers:
- They can be either positive, negative, or zero.
- They can be expressed in decimal form, which either terminates or repeats infinitely.
- Examples include fractions like \frac{3}{4}, integers like 7 (which can be written as \frac{7}{1}), and decimals like 0.25 (which is \frac{1}{4} in fraction form).
The Intriguing World of Irrational Numbers


In stark contrast, irrational numbers are numbers that cannot be expressed as a simple fraction. They possess an endless, non-repeating decimal sequence which makes them impossible to express as a ratio of two integers. These numbers are the wild cards of the number system, including famous examples like \pi (approximately 3.14159), the square root of 2 (approximately 1.41421356), and e (Euler's number, roughly 2.71828).
Key characteristics of irrational numbers:
- They are real numbers that are not rational.
- Their decimal representations go on forever without repeating.
- They are typically represented by symbols or special names due to their unique nature.
Fun Ways to Identify Rational vs. Irrational Numbers

1. The Repeating Decimal Test

The most straightforward way to identify a rational number is by checking if its decimal representation either terminates or repeats.
- Take the number 0.6666... (repeating infinitely). This is \frac{2}{3}, a rational number because its decimal repeats.
- In contrast, \sqrt{2} gives a non-terminating and non-repeating decimal, which signifies an irrational number.
🧮 Note: Not all repeating decimals are rational numbers. For example, the decimal representation of 1/7 (approximately 0.142857142857...) also repeats, but it's a rational number.
2. The Perfect Square Test
This method involves checking if a square root can be expressed as the square of an integer:
- If a number can be squared to give an integer, it's rational. For instance, \sqrt{9} = 3 because 3 \times 3 = 9, so \sqrt{9} is rational.
- If not, such as \sqrt{2} or \sqrt{3}, then the number is irrational. You can't multiply any integer by itself to get 2 or 3.
| Rational Number Examples | Irrational Number Examples |
|---|---|
| \sqrt{1} = 1 | \sqrt{2} ≈ 1.41421356 |
| \sqrt{4} = 2 | \sqrt{3} ≈ 1.7320508 |
| \sqrt{9} = 3 | \sqrt{5} ≈ 2.236068 |

3. The Factorization Method

Another engaging way to distinguish between rational and irrational numbers is through factorization:
- If a number can be broken down into prime factors and then put back together as a ratio of integers, it's rational.
- If the prime factorization reveals an infinite, non-repeating pattern, the number is likely irrational.
Let's look at an example:
- Factorize \frac{8}{15}:
- 8 = 2 × 2 × 2
- 15 = 3 × 5
💡 Note: In practice, this method becomes complex with large numbers or numbers with many prime factors.
4. The Continued Fraction Technique

Continued fractions are a mathematical representation of numbers in which a number is expressed as a fraction with a series of fractions in the denominator. Here's how you can use them to identify irrational numbers:
- Rational numbers have a finite continued fraction.
- Irrational numbers have an infinite, non-repeating continued fraction.
For example, the continued fraction for \pi is [3; 7, 15, 1, 292, 1, \ldots], which goes on indefinitely, indicating that \pi is irrational.
📐 Note: While this method is intriguing, it might be impractical for everyday identification unless you're deeply familiar with continued fractions.
5. The Fundamental Theorem of Algebra

Finally, understanding the Fundamental Theorem of Algebra can help identify irrational numbers in algebraic expressions:
- If an equation has roots that cannot be expressed as ratios of integers, these roots are irrational.
- For example, the equation x^2 - 2 = 0 has solutions \sqrt{2} and -\sqrt{2}, both of which are irrational because they can't be expressed as fractions.
This theorem essentially helps in recognizing that complex polynomials can lead to irrational roots, thereby identifying irrational numbers within algebraic contexts.
This exploration into rational and irrational numbers offers a nuanced understanding of how numbers work, and how we can playfully interact with the math in our daily lives. From checking repeating decimals to examining the behavior of square roots or applying advanced techniques like continued fractions, there's a method to suit everyone's curiosity and mathematical level.
In summary, rational numbers are those that can be expressed as simple fractions or have decimal representations that terminate or repeat. Irrational numbers, on the other hand, are infinitely non-repeating and cannot be written as a simple fraction. By using these various techniques, you can easily identify which category a given number falls into, making mathematics both fun and accessible.
What is the difference between a rational and an irrational number?

+
The primary difference is that a rational number can be expressed as a ratio of two integers, whereas an irrational number cannot. Rational numbers have decimal representations that either terminate or repeat, while irrational numbers have non-terminating, non-repeating decimals.
Why is the square root of 2 an irrational number?
+
The square root of 2 is irrational because it cannot be expressed as a ratio of two integers. When you try to express (\sqrt{2}) as a fraction, the decimal representation goes on forever without repeating or terminating.
Can you name some famous irrational numbers?

+
Some famous irrational numbers include (\pi), (\sqrt{2}), (\sqrt{3}), and (e) (Euler’s number). These numbers are well-known for their non-repeating and non-terminating decimal sequences.