5 Fun Worksheets to Master Rational and Irrational Numbers

Introduction to Rational and Irrational Numbers

Welcome to our exploration of rational and irrational numbers, a fundamental concept in mathematics. Understanding these numbers is essential for anyone looking to master algebra, geometry, or even advanced math topics. In this blog, we dive into five fun and engaging worksheets that will help students of all ages cement their understanding of these number types. By the end, you’ll have the tools to tackle any problem involving rational and irrational numbers with confidence.
Why Rational and Irrational Numbers Matter

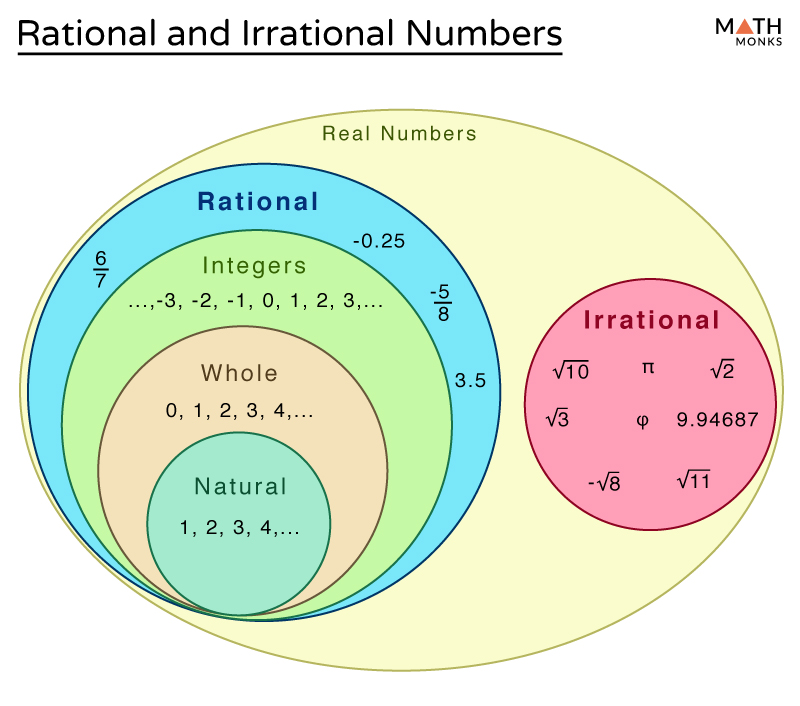
Rational numbers can be expressed as a fraction or ratio of two integers, like 1⁄2, -3, or 7⁄5. They include all integers, fractions, and any terminating or repeating decimal. Irrational numbers, however, can’t be written as a simple fraction; their decimal expansions neither terminate nor repeat. Notable examples are π, e, and √2.
Understanding these differences is vital:
- To solve equations involving roots and surds.
- For geometric calculations where irrational numbers often appear.
- In real-world applications like architecture, engineering, and computer science.
Worksheet 1: Identifying Rational and Irrational Numbers


This worksheet starts with the basics:
- List numbers: Provide a mix of integers, fractions, and decimal numbers. Students will classify each number as rational or irrational.
- Real-life examples: Include numbers from real-world scenarios like the height of a building or the width of a river.
- Challenge: Introduce more complex numbers like π, square roots, and repeating decimals.
📝 Note: Encourage students to explain their classification, enhancing their understanding of each number's properties.
Worksheet 2: Converting Fractions and Decimals

Converting between different forms of rational numbers is a core skill:
- Convert fractions to decimals and vice versa.
- Identify which decimals are rational and which are irrational by their behavior.
- Learn about repeating decimals and how they relate to fractions.
Key Activities:

| Action | Examples |
|---|---|
| Convert to decimal | 1⁄3, 5⁄6, 7⁄8 |
| Identify rational/irrational | √3, 1.41421356… |
| Repeating Decimals | 0.666…, 0.142857142857… |

🧮 Note: Use this worksheet to explore the concept of “rational” in decimals, which can be particularly illuminating for visual learners.
Worksheet 3: Arithmetic Operations with Rational and Irrational Numbers
Understanding how to perform operations on these numbers:
- Add, subtract, multiply, and divide rational numbers.
- Add and subtract irrational numbers.
- Understand the rules about multiplying or dividing irrational numbers.
Exercises:

- Calculate 2√2 + √2.
- Subtract √3 from 5π.
- Multiply π by π (π²).
✅ Note: Emphasize that the product of two rational numbers is always rational, and the product of two irrational numbers might be either rational or irrational.
Worksheet 4: Rational and Irrational Numbers in Geometry

Geometry provides a rich context for understanding these numbers:
- Calculate the hypotenuse of right triangles using Pythagorean theorem.
- Explore the area of circles with π.
- Investigate the golden ratio and its irrationality.
Geometry Problems:

- Find the length of the diagonal in a square with sides of length 3.
- Calculate the circumference of a circle with a radius of 5.
- Explore the Fibonacci sequence and the golden ratio.
📐 Note: Encourage students to visualize problems using diagrams or models to better grasp how irrational numbers appear in geometry.
Worksheet 5: Proofs and Properties of Rational and Irrational Numbers

Mathematical proofs provide insight into the nature of these numbers:
- Prove that √2 is irrational.
- Explore the fact that the sum or difference of a rational and an irrational number is irrational.
- Investigate that the product or quotient of a rational and an irrational number is irrational.
Proof-based Exercises:

- Prove that the sum of a rational and an irrational number is irrational.
- Show that π + √2 is irrational.
- Verify that the product of a rational and an irrational number is irrational.
✏️ Note: This worksheet enhances logical thinking and provides a deeper understanding of number theory.
In this post, we've explored five engaging worksheets designed to help students grasp the concept of rational and irrational numbers. From identification and conversion to geometric applications and proofs, each worksheet offers a different facet of learning. These exercises not only boost confidence in mathematics but also reveal the beauty and interconnectedness of numbers in our world.
What’s the difference between rational and irrational numbers?

+
Rational numbers can be expressed as a fraction of two integers (e.g., 1⁄2 or -5). Irrational numbers, like π or √2, cannot be expressed as simple fractions, and their decimal expansions neither terminate nor repeat.
Why are irrational numbers important in real life?

+
Irrational numbers play a crucial role in fields like engineering, architecture, physics, and more where precise measurements and calculations are needed, often involving π, e, and square roots.
Can you list some common irrational numbers?

+
Yes, here are some common irrational numbers: √2 (square root of 2), √3, π (pi), e (Euler’s number), and the golden ratio (φ≈1.618).