Radians to Degrees: Free Conversion Worksheet

In the realm of mathematics, particularly trigonometry and calculus, understanding the relationship between radians and degrees is essential. This post serves as a comprehensive guide to converting radians to degrees and vice versa, providing you with free, downloadable worksheets to practice this crucial skill. Whether you're a student, a teacher, or just someone interested in math, this guide will help you master the conversion process, improve your math proficiency, and understand the underlying concepts.
Why Convert Between Radians and Degrees?
Radians and degrees are two units of measuring angles:
- Degrees are what most people are familiar with. A full circle equals 360 degrees, with each degree representing 1/360th of a circle.
- Radians, on the other hand, are used in more advanced mathematical settings. A full circle equals
2\pi radians , where 1 radian is the angle subtended at the center of a circle by an arc with the same length as the radius of the circle.
Here are reasons why converting between these units is necessary:
- To solve trigonometric identities and equations where angles might be given or needed in different units.
- Some fields like physics and engineering often use radians for calculations due to their simplicity in calculus.
- Understanding the conversion helps in interpreting various mathematical functions and graphs.

The Conversion Formula
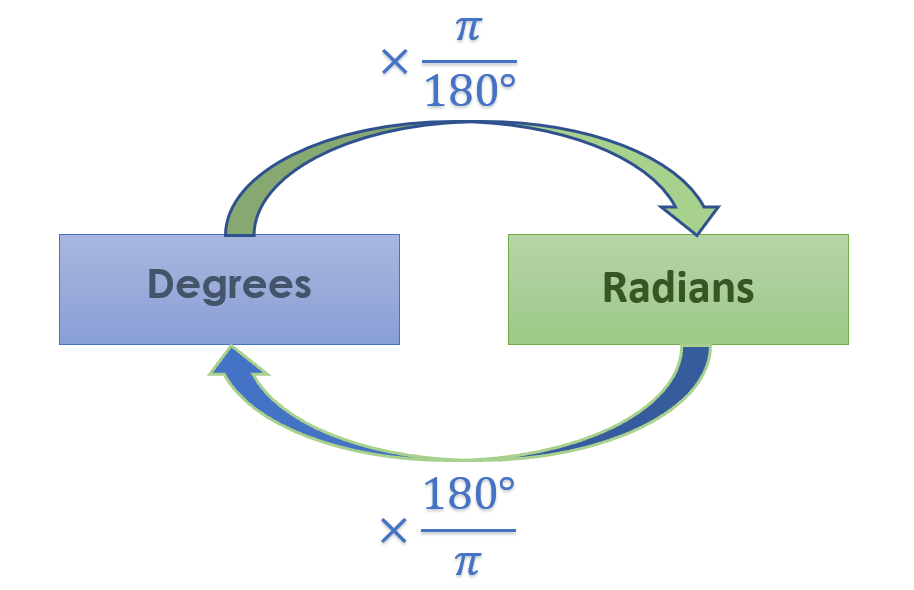
To convert from radians to degrees, use the following formula:
degrees = (radians * 180) / π
To convert from degrees to radians, the inverse is applied:
radians = (degrees * π) / 180
Step-by-Step Guide to Convert Radians to Degrees

- Identify the value in radians you wish to convert.
- Multiply this value by 180.
- Divide the result by π (approximately 3.14159).
- The result is the equivalent value in degrees.
💡 Note: Ensure your calculator is set to ‘radians’ mode when working with these conversions.
Free Conversion Worksheet
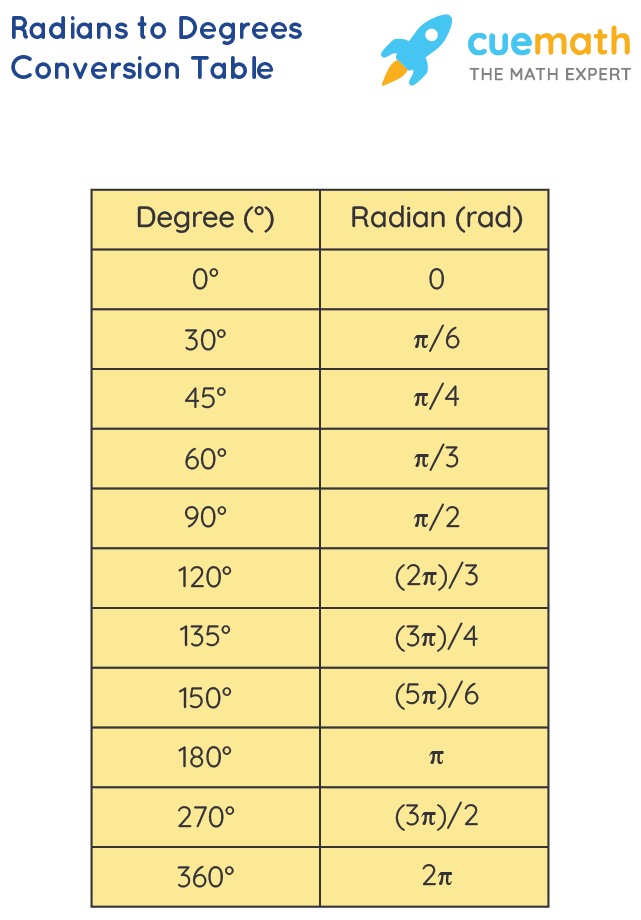
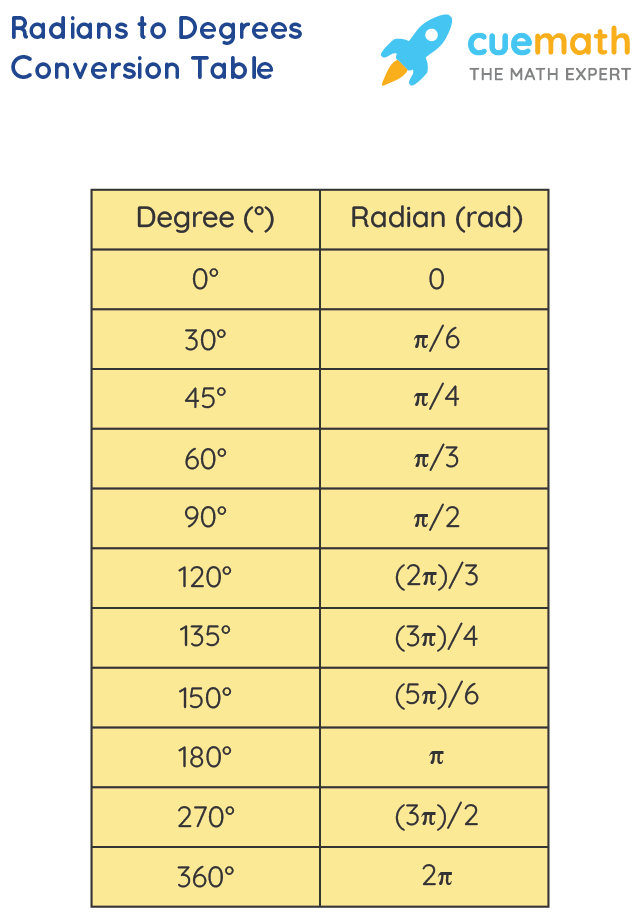
Below is a table with exercises for practicing radian to degree conversions:
| Radians | Degrees |
|---|---|
| π/2 | |
| π/4 | |
| 2π/3 |

💡 Note: You can download the full worksheet with solutions from the links at the end of this article.
Practical Examples

Here are some examples to illustrate the conversion:
- Example 1: Convert π/6 radians to degrees.
- Step 1: π/6 * 180 = 30π
- Step 2: 30π / π = 30
- π/6 radians is equivalent to 30 degrees.
- Example 2: Convert 5π/9 radians to degrees.
- Step 1: 5π/9 * 180 = 300π/3
- Step 2: 300π/3 / π = 100
- 5π/9 radians is equivalent to 100 degrees.
💡 Note: When dealing with fractions of π, it's often more convenient to leave π in the equation until the last step of division to reduce calculation errors.
Common Mistakes in Radian to Degree Conversion

Here are some common pitfalls to watch out for:
- Incorrect Calculator Setting: Not changing the calculator to radians mode.
- Multiplication/Division Errors: Mixing up the order of operations in the conversion formula.
- Approximation: Using approximations for π or not carrying through exact values, leading to errors.
Converting Degrees to Radians

The process of converting degrees to radians is essentially the inverse of radians to degrees:
- Multiply the degree value by π.
- Divide by 180.
💡 Note: When converting degrees to radians, if you end up with a fraction, simplify it before converting to radians to maintain precision.
Final Thoughts

Converting between radians and degrees is a fundamental skill that opens up numerous pathways in both theoretical and applied mathematics. The ability to seamlessly switch between these units not only enhances your problem-solving capabilities but also deepens your understanding of how angles relate to different mathematical contexts. With the provided worksheets and practical examples, you’re now equipped to practice this conversion until it becomes second nature.
What is the benefit of using radians over degrees?
+
Radians simplify many calculus operations because they measure angles directly related to the arc length of the circle’s circumference. This relationship makes trigonometric functions like sine, cosine, and tangent more intuitive and easier to differentiate or integrate.
Can I use approximations of π when converting?
+
Yes, you can use approximations of π (like 3.14159) for simple conversions, but for precision work or when exact values are required, keeping π in the calculation until the end helps minimize errors.
How often do professionals in STEM fields use these conversions?

+
In fields like engineering, physics, and computer graphics, understanding radians is crucial as calculations are often performed in radians. However, the ability to convert and interpret results in degrees is also frequently needed.