Mastering Quadrilaterals: 5 Essential Coordinate Plane Tips
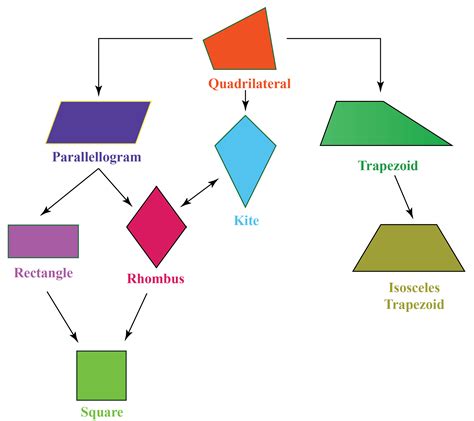
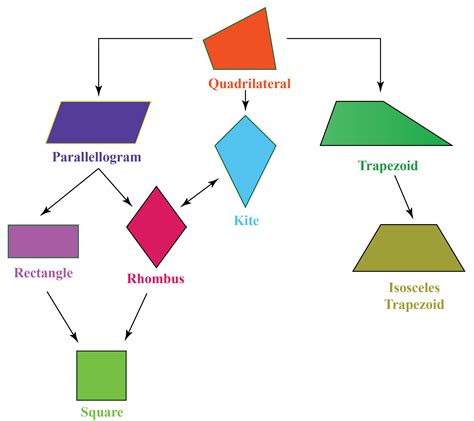
Understanding Quadrilaterals in the Coordinate Plane
Quadrilaterals are a fundamental concept in geometry, and when it comes to working with them in the coordinate plane, there are several essential tips to keep in mind. Whether you’re a student, teacher, or simply looking to improve your math skills, mastering quadrilaterals in the coordinate plane can help you tackle a wide range of problems with confidence. In this article, we’ll explore five essential tips to help you work with quadrilaterals in the coordinate plane.
Tip 1: Plotting Points and Identifying Quadrilateral Shapes

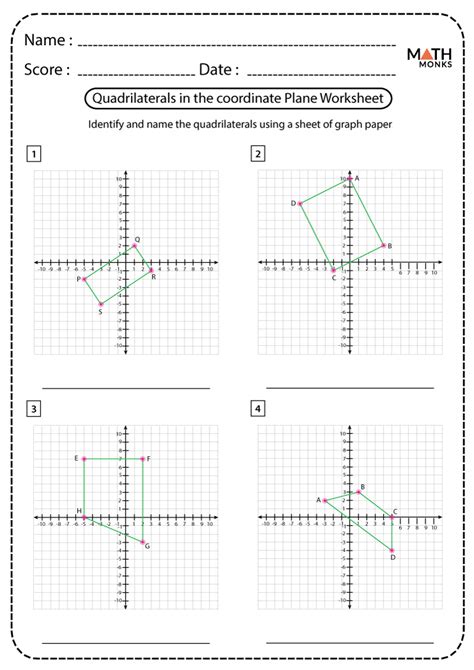
When working with quadrilaterals in the coordinate plane, it’s essential to start by plotting the points that define the shape. This can be done by using the coordinates (x, y) to locate the points on the grid. Once you’ve plotted the points, you can use the coordinates to identify the type of quadrilateral you’re dealing with.
For example, if the points are (2, 3), (4, 5), (6, 3), and (4, 1), you can use the coordinates to determine that the shape is a trapezoid. Remember to always label the points and the quadrilateral shape to ensure clarity.
Tip 2: Finding the Midpoint of a Line Segment
The midpoint of a line segment is an essential concept in coordinate geometry, and it’s particularly useful when working with quadrilaterals. To find the midpoint of a line segment, you can use the midpoint formula:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
For example, if you want to find the midpoint of a line segment with endpoints (3, 4) and (5, 6), you can use the midpoint formula to get:
Midpoint = ((3 + 5)/2, (4 + 6)/2) = (4, 5)
The midpoint formula is a valuable tool for working with quadrilaterals, so be sure to memorize it.
Tip 3: Finding the Slope of a Line Segment
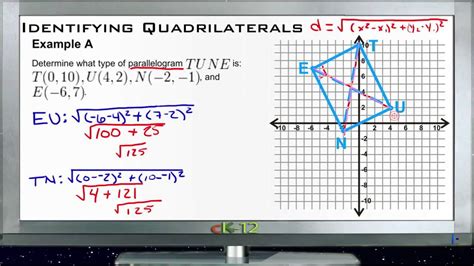
The slope of a line segment is another essential concept in coordinate geometry, and it’s particularly useful when working with quadrilaterals. To find the slope of a line segment, you can use the slope formula:
Slope = (y2 - y1)/(x2 - x1)
Where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
For example, if you want to find the slope of a line segment with endpoints (2, 3) and (4, 5), you can use the slope formula to get:
Slope = (5 - 3)/(4 - 2) = 1
The slope formula is a valuable tool for working with quadrilaterals, so be sure to memorize it.
Tip 4: Using the Distance Formula to Find the Length of a Side
The distance formula is a useful tool for finding the length of a side of a quadrilateral. To use the distance formula, you can plug in the coordinates of the endpoints of the side into the formula:
Distance = √((x2 - x1)^2 + (y2 - y1)^2)
Where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the side.
For example, if you want to find the length of a side with endpoints (3, 4) and (5, 6), you can use the distance formula to get:
Distance = √((5 - 3)^2 + (6 - 4)^2) = √(4 + 4) = √8
The distance formula is a valuable tool for working with quadrilaterals, so be sure to memorize it.
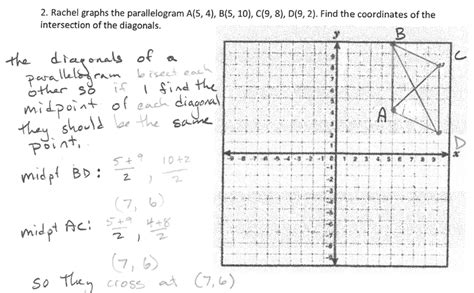
Tip 5: Using the Coordinate Plane to Prove Properties of Quadrilaterals
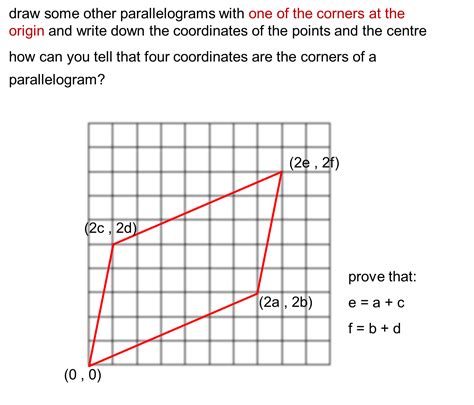
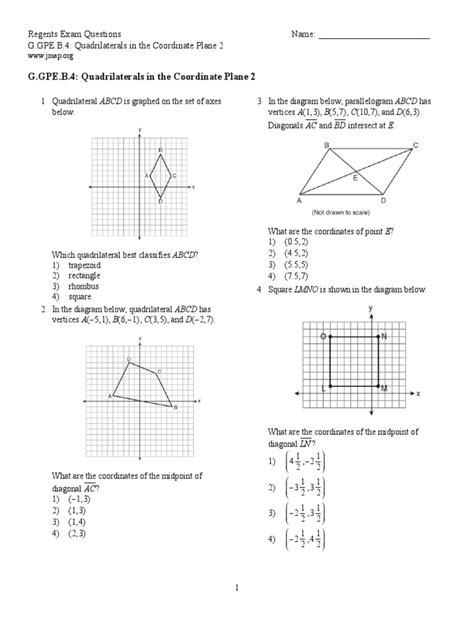
The coordinate plane can be a powerful tool for proving properties of quadrilaterals. By plotting the points that define a quadrilateral and using the coordinates to find the midpoints, slopes, and lengths of the sides, you can prove a wide range of properties.
For example, you can use the coordinate plane to prove that the diagonals of a rectangle bisect each other, or that the opposite sides of a parallelogram are equal.
By mastering the coordinate plane, you can tackle even the toughest quadrilateral problems with confidence.
📝 Note: When working with quadrilaterals in the coordinate plane, it's essential to be precise and accurate with your calculations. Double-check your work to ensure that you're getting the correct answers.
In conclusion, mastering quadrilaterals in the coordinate plane requires a combination of theoretical knowledge and practical skills. By following these five essential tips, you can improve your understanding of quadrilaterals and become more confident in your ability to work with them.
What is the midpoint formula?

+
The midpoint formula is a mathematical formula used to find the midpoint of a line segment. It is given by: Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
How do I find the slope of a line segment?
+
The slope of a line segment can be found using the slope formula: Slope = (y2 - y1)/(x2 - x1)
What is the distance formula?
+
The distance formula is a mathematical formula used to find the distance between two points in the coordinate plane. It is given by: Distance = √((x2 - x1)^2 + (y2 - y1)^2)
Related Terms:
- gpe quadrilateral coordinate plane
- coordinate proof quadrilaterals
- quadrilateral mathematics
- coordinate plane of a quadrilateral
- quadrilaterals in gpe
- coordinates of a quadrilateral