5 Tips to Master Quadrilateral Proofs Fast
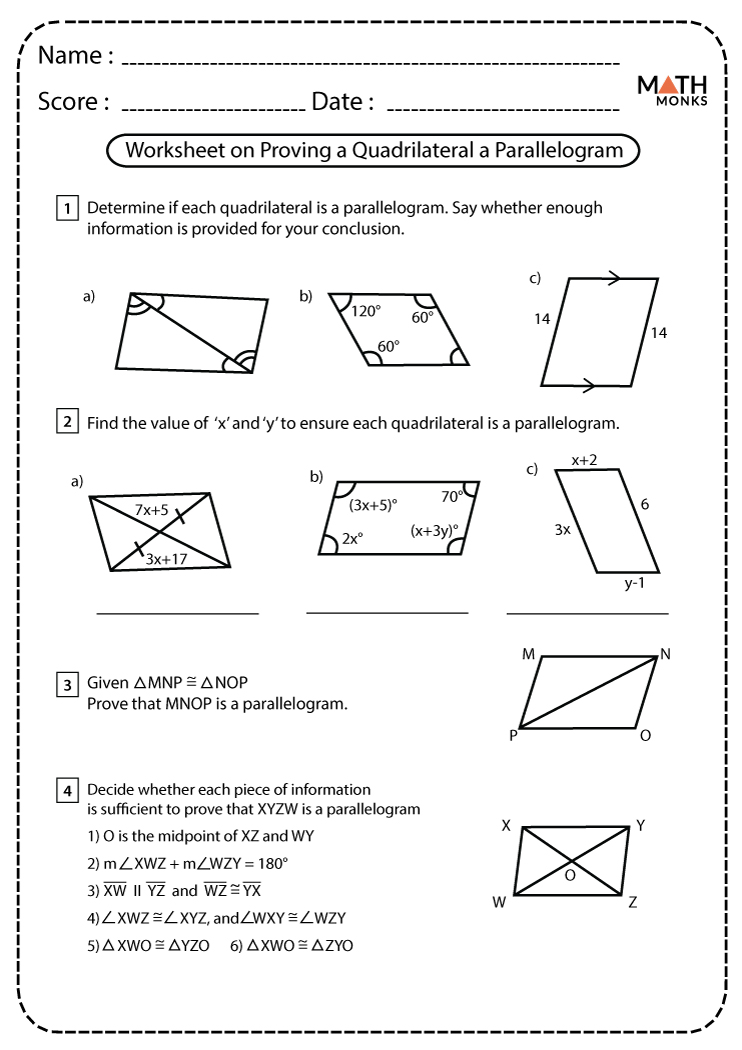
Mastering quadrilateral proofs can be a daunting task for many students in geometry. However, with the right techniques and practice, you can quickly become proficient. Here are five essential tips to help you master quadrilateral proofs faster:
Understand the Basics
Before diving into complex proofs, ensure you have a solid grasp of the fundamental properties of quadrilaterals:
- Parallelograms: Opposite sides are parallel and equal; opposite angles are equal.
- Rectangles: All angles are right angles; opposite sides are equal.
- Squares: All sides are equal; all angles are right angles.
- Rhombuses: All sides are equal; diagonals bisect each other at 90 degrees.
- Trapezoids: One pair of opposite sides are parallel.
- Kites: Two pairs of adjacent sides are equal; one diagonal bisects the other at 90 degrees.
Image here
⚡ Note: Make sure to memorize these properties as they are the building blocks for quadrilateral proofs.
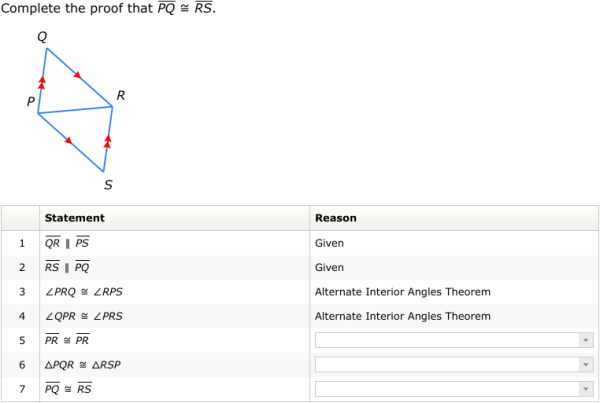
Create Diagrams and Visual Aids

Visualization is key in geometry proofs. When tackling a quadrilateral proof:
- Always draw a diagram to visualize the problem. Label all known sides, angles, and vertices.
- Use different colors or styles for different quadrilaterals to distinguish their properties visually.
- Draw in diagonals to see the relationships between angles and sides more clearly.
| Quadrilateral | Diagonals |
|---|---|
| Parallelogram | Bisect each other |
| Rectangle | Equal in length |
| Square | Bisect at 90° |
| Rhombus | Bisect each other at 90° |

Image here
👉 Note: Diagrams help to avoid mistakes by providing a visual map of your proof process.
Use Theorems and Postulates
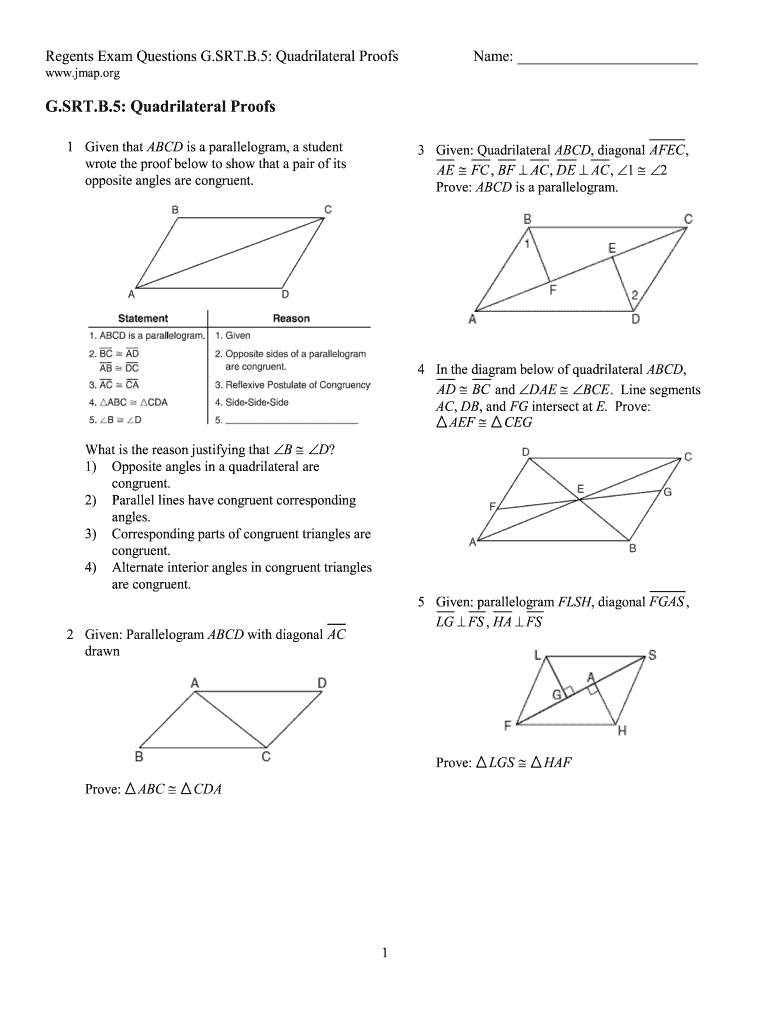
Geometry is built upon a set of postulates and theorems. For quadrilateral proofs:
- Apply the Midpoint Theorem, Perpendicular Bisector Theorem, or the Converse of the Base Angles Theorem where applicable.
- Familiarize yourself with theorems like the Isosceles Triangle Theorem, which can be useful in proving properties of kites or rhombuses.
- Use the concept of congruent triangles to establish equalities between sides or angles.
When using these tools:
- State the theorem or postulate before applying it.
- Explain how the conditions of the theorem are met in your problem.
Practice with Examples

Practice makes perfect, especially in proofs. Here are some steps to follow:
- Start with simpler proofs and work your way up to more complex ones.
- Review solved examples from textbooks or online resources to understand different methods and reasoning paths.
- Engage in problem-solving sessions where you and peers attempt proofs together, discussing strategies and alternative approaches.
Here is a simple example:
Example: Prove that the diagonals of a rectangle are equal in length.
- Draw a rectangle ABCD.
- Since ABCD is a rectangle, all angles are right angles.
- Let AC and BD be the diagonals. By the property of rectangles, diagonal AC bisects BD at point O.
- Now, consider triangles AOB and COD. They are congruent by SAS (Side-Angle-Side) since AO=CO, BO=DO, and ∠AOB=∠COD=90°.
- By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), AC=BD.
Break Down Complex Proofs
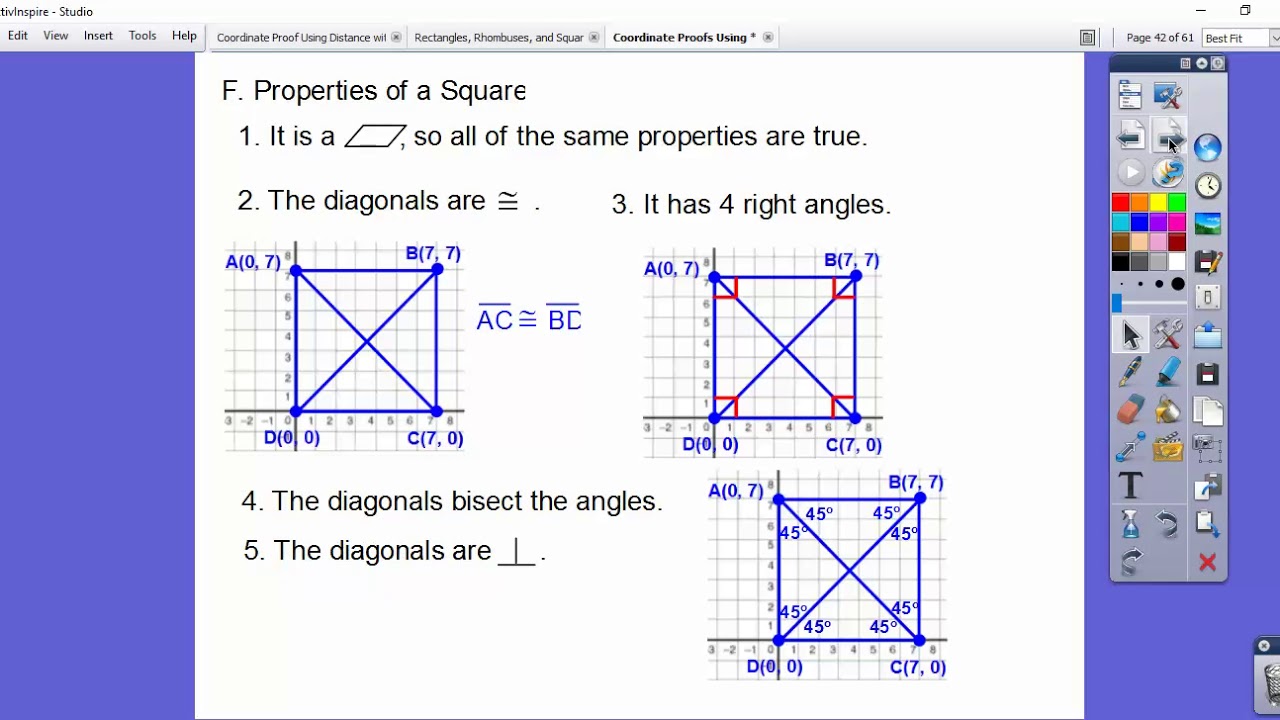
When faced with a complicated proof:
- Read the problem statement several times to understand what is given and what needs to be proven.
- Identify the type of quadrilateral involved and its properties that might help in the proof.
- Use sub-proofs to establish intermediate results that lead to the final proof.
Here are some strategies:
- Top-Down Approach: Start with what needs to be proved and work backward to the knowns.
- Bottom-Up Approach: Start with the given information and deduce forward to the statement to be proven.
- Highlighting: Use color-coding or annotations to highlight relationships and dependencies in the proof process.
In summary, mastering quadrilateral proofs involves understanding the basics, employing visual aids, utilizing geometry theorems, practicing with examples, and methodically breaking down complex problems. By following these steps, you’ll gain the confidence and skills needed to tackle any quadrilateral proof with ease.
What are the key properties I need to know about quadrilaterals for proofs?

+
Key properties include: Parallelograms (opposite sides parallel and equal, opposite angles equal), Rectangles (all angles right), Squares (all sides equal, all angles right), Rhombuses (all sides equal), Trapezoids (one pair of opposite sides parallel), and Kites (adjacent sides equal). Understanding these will form the basis for most proofs.
How can diagrams help in proving quadrilateral properties?

+
Diagrams visually represent the given and required conditions of a proof. They help in visualizing relationships between sides, angles, and diagonals, making it easier to spot applicable theorems or postulates.
What are some common mistakes in quadrilateral proofs?

+
Common mistakes include: assuming properties not given in the problem, incorrect use of congruence or similarity, and not proving intermediate steps which are critical for the proof. Careful diagramming and methodical reasoning can avoid these pitfalls.