Explore the Quadrilateral Family Tree with Our Worksheet
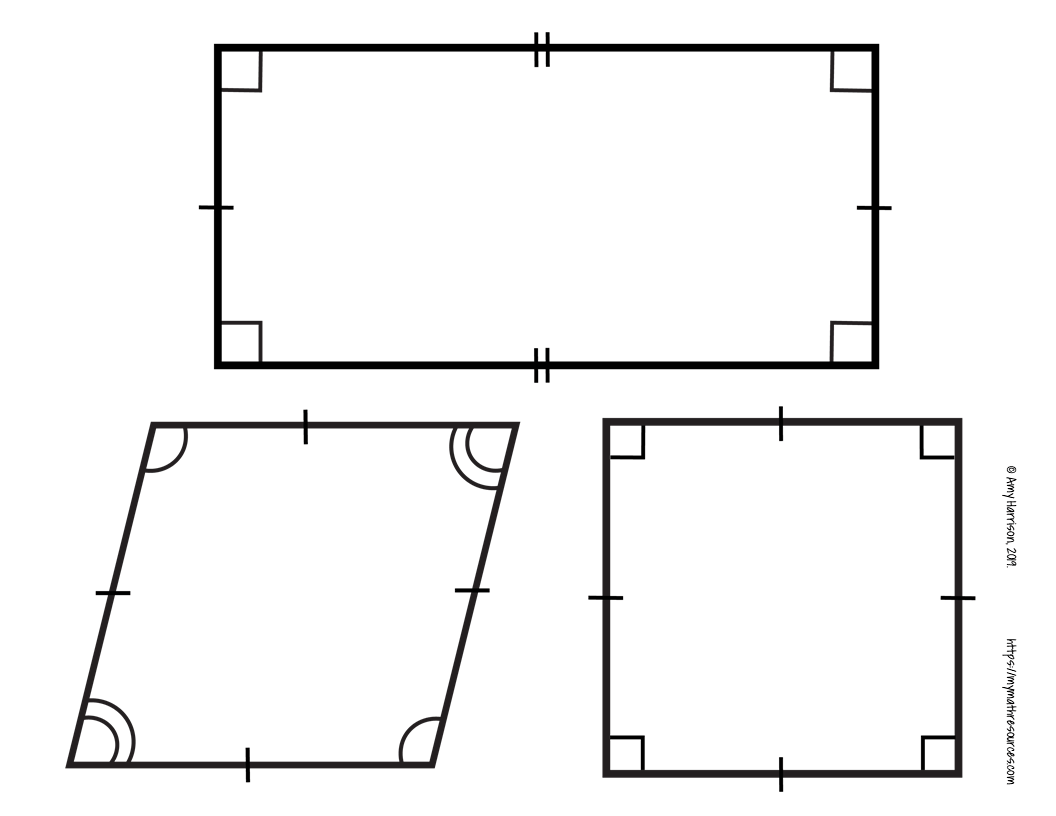
In the vast landscape of mathematics, geometry holds a special place where shapes dance and forms interlink to create patterns and formulas we use in our daily life. One branch of this fascinating subject is the study of quadrilaterals. The quadrilateral family tree is not just a list of different four-sided figures; it's a rich tapestry of relationships, properties, and classifications that make geometry an endlessly intriguing subject. Let's explore this family with our worksheet, designed to help you understand the connections and differences between various types of quadrilaterals.
The Base of the Family: The Quadrilateral

A quadrilateral is any four-sided polygon. It serves as the root of our family tree, from which all other types branch out. Here are some basic properties:
- Four vertices.
- Four sides that connect those vertices.
- Interior angles sum up to 360 degrees.
🔍 Note: Quadrilaterals are versatile and can form from various combinations of lines and angles.
Children of the Quadrilateral: Parallelograms

From the base, we move up to the parallelogram, which has these characteristics:
- Opposite sides are equal in length.
- Opposite angles are congruent.
- Opposite sides are parallel.
| Type | Properties |
|---|---|
| Rhombus | All sides equal, diagonals bisect each other at 90 degrees. |
| Rectangle | All angles are right angles (90 degrees). |

🔎 Note: The diagonal properties of a parallelogram are unique; they bisect each other, but not necessarily at right angles, unlike in a rhombus.
Descendants of Parallelograms

The Special Parallelogram: Rectangle

The rectangle adds to the parallelogram traits:
- All interior angles are right angles.
- Diagonals are equal in length.
🔐 Note: Remember, a rectangle is a special kind of parallelogram where the extra condition of having all angles right helps in identifying it.
The Rhombus: A Close Relative

Rhombuses are special in their own way:
- All sides are of equal length.
- Diagonals bisect the angles of the rhombus, forming four right-angled triangles.
🔏 Note: The diagonals of a rhombus don't have to be of the same length; it's the sides that are the key.
The Curious Case of the Square
The square unites properties from both rectangle and rhombus:
- All sides are equal (like a rhombus).
- All angles are right angles (like a rectangle).
The Opposites: Trapezoids

On another branch, we have trapezoids, characterized by:
- At least one pair of parallel sides.
- They can be isosceles if the non-parallel sides are equal in length.
Here's where it gets a bit different:
- Isosceles Trapezoid: Non-parallel sides are equal, with diagonals also equal.
- Right Trapezoid: Contains at least two right angles.
Final Thoughts

Delving into the world of quadrilaterals provides a thrilling journey through geometry. Our worksheet acts as a guide, helping you to understand how these shapes relate to one another through a blend of intriguing properties, classifications, and mathematical relationships. You've explored the foundational quadrilateral, ventured into the realm of parallelograms, discovered the unique characteristics of rectangles, rhombuses, and squares, and even explored the different flavors of trapezoids. Remember, the beauty of geometry lies in the patterns and symmetry that connect different elements, making even the most complex shapes understandable through simple rules.
What makes a quadrilateral special?

+
A quadrilateral’s uniqueness lies in its diverse forms and the properties that define them. Its four sides can create a variety of shapes, each with distinct characteristics, making it a versatile and rich area of study in geometry.
Can a square be considered a rectangle?

+
Absolutely. A square is a special rectangle because it satisfies all the rectangle’s properties: all angles are right angles, and diagonals are equal. In this case, the square also adds the extra condition of all sides being equal, making it a more specialized type of rectangle.
How do you differentiate between a rhombus and a kite?

+
A rhombus has all sides equal, whereas a kite has two pairs of adjacent sides equal. Also, while diagonals of a rhombus bisect each other at right angles, a kite’s diagonals are perpendicular, with one bisecting the other.