5 Tips to Master Quadratic Functions Worksheet

Quadratic functions are a cornerstone of algebra and are essential for a wide range of applications in mathematics, science, physics, engineering, economics, and more. Understanding how to manipulate and solve quadratic equations is not just about solving complex mathematical problems; it's also about fostering analytical thinking, problem-solving skills, and a deeper appreciation of the patterns found in nature and technology. Here are five comprehensive tips to help you master quadratic functions through worksheet practice, tailored to enhance both your conceptual understanding and practical skills.
1. Grasp the Basics: Understand the Standard and Vertex Forms

Quadratic functions can be expressed in multiple forms, each with its own advantages. Let's delve into:
- Standard Form: ax^2 + bx + c = 0, where a, b, and c are constants.
- Here, a determines the direction of the parabola (up if a > 0, down if a < 0).
- b and c affect the position and opening of the parabola.
- Vertex Form: a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
- This form directly shows the vertex, making it easy to find the minimum or maximum value of the quadratic function.
Worksheet Practice: Convert quadratic functions between standard and vertex forms. Start with simple equations and gradually increase complexity.
2. Solve Quadratic Equations Using Various Methods

Understanding different solution methods is key to mastering quadratic equations:
- Factoring: Factor the quadratic to find roots when possible.
- Completing the Square: Transform the equation into a perfect square plus a constant.
- Quadratic Formula: Use x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} for all types of quadratics.
- Graphical Method: Plot the quadratic on a graph to visually find the roots.
Worksheet Practice: Allocate different sections of the worksheet for each method. Start with equations that can be easily solved by factoring, then move to ones requiring the quadratic formula or completing the square.
📚 Note: Always double-check your solutions by substituting them back into the original equation to ensure accuracy.
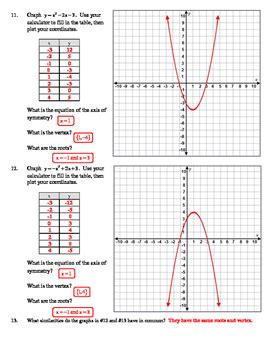
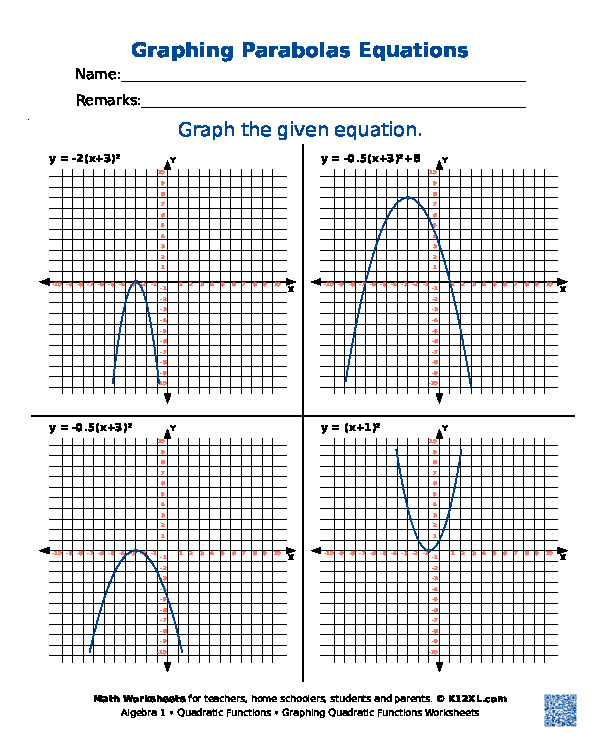
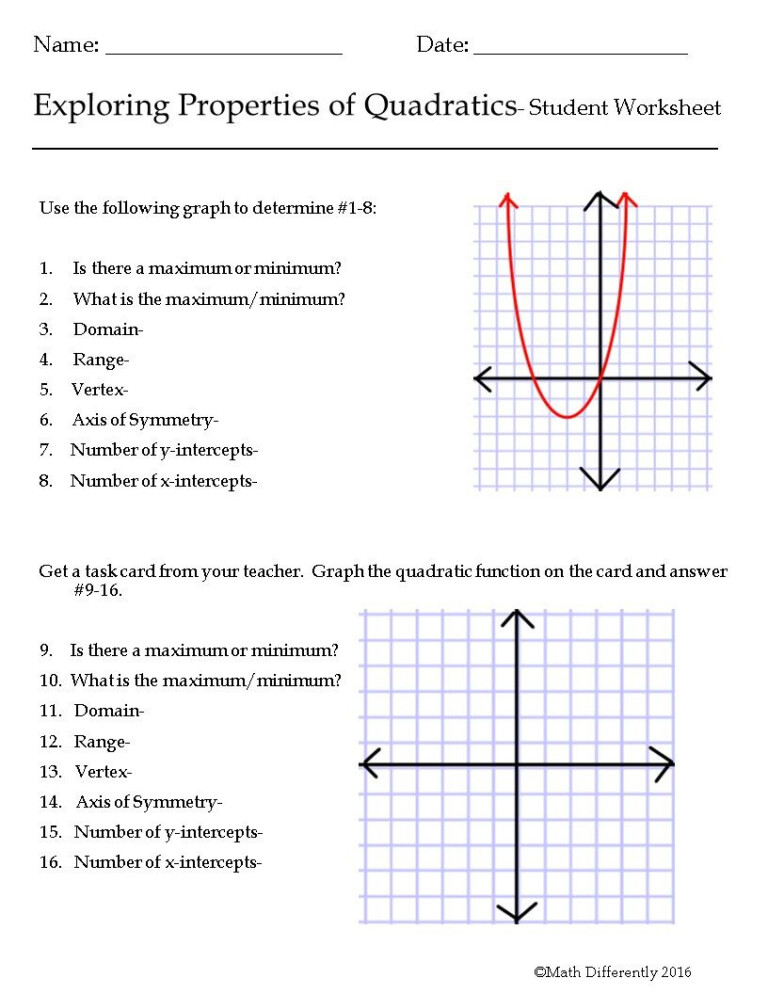
3. Analyze Quadratic Functions Graphically

Graphs provide a visual representation of quadratic functions, allowing for insights into their behavior:
- Vertex: The highest or lowest point of the parabola.
- Intercept Points: Where the graph intersects the x and y-axes.
- Direction of Opening: Positive or negative a determines this.
| Characteristic | Description |
|---|---|
| Vertex | The point (h, k) in vertex form or -\frac{b}{2a} in standard form. |
| X-intercept(s) | Where the function equals zero, giving the roots or solutions to the equation. |
| Y-intercept | The value of the function when x = 0, or simply c. |
| Axis of Symmetry | The line x = h or -\frac{b}{2a} |

Worksheet Practice: Plot various quadratic functions and identify key features. Use different forms of the equation to practice transformation of the parabola.
4. Real-World Applications and Word Problems

Quadratic functions are not just theoretical constructs; they are practical tools:
- Model physical phenomena like projectile motion, where height h(t) = -16t^2 + v_0t + h_0.
- Optimize costs or profits in economics.
- Analyze or predict the spread of diseases in epidemiology.
Worksheet Practice: Include word problems that require setting up quadratic equations to represent real-world scenarios, solving them, and interpreting the solutions.
🔬 Note: Always consider the units in real-world problems to maintain practical relevance of your solutions.
5. Review, Reflect, and Seek Feedback

Mistakes are opportunities to learn. Regular review is crucial for mastery:
- Go over past worksheets and quizzes to see where errors were made.
- Reflect on different methods used to solve quadratic equations.
- Seek feedback from teachers, peers, or online communities.
Worksheet Practice: Design worksheets that incorporate past mistakes or challenging concepts for self-assessment and improvement.
Mastering quadratic functions requires not only understanding the underlying mathematics but also the ability to apply this knowledge creatively. Through consistent practice with quadratic functions worksheets, you'll develop a robust understanding of these essential mathematical concepts. This preparation will enable you to tackle quadratic equations with confidence, ready to solve problems both in academia and in real-world situations where such mathematical tools are essential.
Why are quadratic functions important in mathematics?
+
Quadratic functions are fundamental because they represent the simplest form of polynomial equations beyond linear equations, offering insights into curves, optimization, and growth patterns in various fields like physics, economics, and biology.
What are the different methods to solve a quadratic equation?
+
There are several methods to solve quadratic equations:
- Factoring: When the equation can be factored into binomials.
- Completing the Square: To rewrite the quadratic in perfect square form.
- Quadratic Formula: Applicable to all quadratic equations.
- Graphical Method: By plotting and finding intersections.
Can quadratic functions have more than two roots?
+
Quadratic functions in standard form can have at most two real roots. If the discriminant ((b^2 - 4ac)) is zero, there is one real root (a double root), and if negative, there are no real roots (but two complex roots). Quadratic functions do not have more than two roots.



