Pythagorean Triples Worksheet: Unlock the Mystery

Exploring the Wonders of Pythagorean Triples

Pythagorean Triples are not just a part of mathematical theory but a treasure trove for both educators and students. Their unique properties provide an entry point into the world of number theory and algebra. This comprehensive guide will walk you through understanding and working with Pythagorean Triples, offering exercises and tips to demystify this fascinating mathematical concept.
What Are Pythagorean Triples?
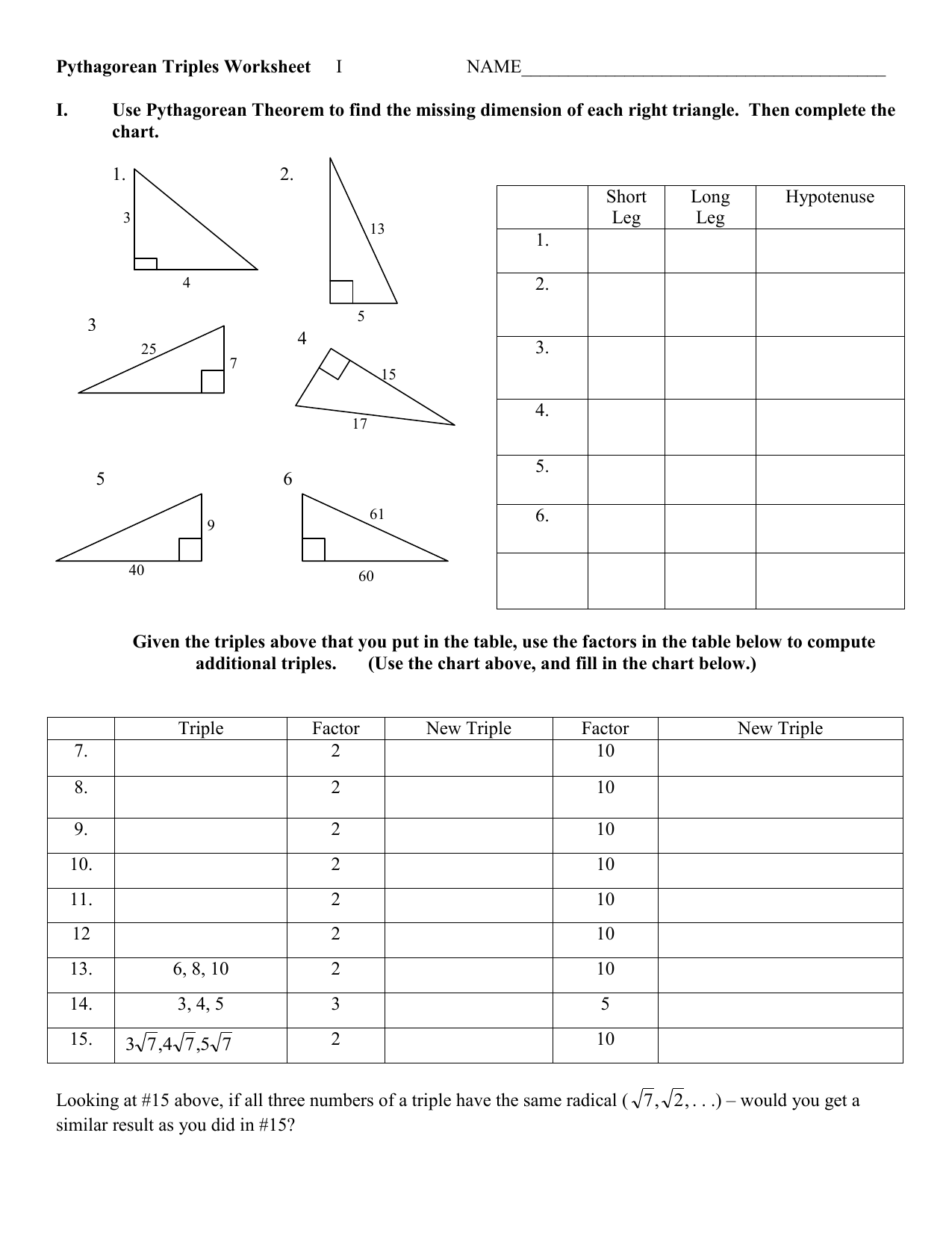
A Pythagorean Triple is a set of three natural numbers (a), (b), and (c), such that (a^2 + b^2 = c^2). These triples are named after the ancient Greek mathematician Pythagoras because of their connection to the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of squares of the other two sides. Here are some well-known examples:
- 3, 4, 5 (where (3^2 + 4^2 = 9 + 16 = 25 = 5^2))
- 5, 12, 13
- 8, 15, 17
- 7, 24, 25
Generating Pythagorean Triples

There are multiple ways to generate Pythagorean Triples. Let’s explore some of these methods:
Euler’s Formula

Euler’s formula provides a method to generate an infinite number of Pythagorean Triples:
If (m) and (n) are two positive integers with (m > n), then the Pythagorean Triple can be found using the following formulas:
- (a = m^2 - n^2)
- (b = 2mn)
- (c = m^2 + n^2)
💡 Note: Euler’s formula also guarantees that (a), (b), and (c) are coprime if (m) and (n) are coprime and of different parity (one even, one odd).
Primitive Triples

Primitive Pythagorean Triples are those in which (a), (b), and (c) have no common factor other than 1. They can be generated by:
- Picking any two natural numbers (m) and (n) such that (m > n), (m - n) is odd, and (\text{gcd}(m, n) = 1).
- Using (a = 2mn), (b = m^2 - n^2), and (c = m^2 + n^2).
Worksheet: Engaging with Pythagorean Triples

To better understand Pythagorean Triples, here’s a worksheet designed to challenge and reinforce your knowledge:
1. Identify Pythagorean Triples

Identify which of the following sets are Pythagorean Triples:
- (6, 8, 10)
- (5, 12, 13)
- (9, 40, 41)
2. Generate Triples Using Euler’s Formula

Using Euler’s formula where (m = 3) and (n = 1):
- Calculate (a), (b), and (c).
3. Creating Your Own

Choose your own (m) and (n) to generate a new Pythagorean Triple. Remember to choose coprime numbers with one even and one odd.
📝 Note: Practice not only enhances understanding but also fosters a deeper appreciation for mathematical patterns.
Incorporating Pythagorean Triples into Real-Life Scenarios

Understanding Pythagorean Triples can be more than just theoretical; they appear in many real-world applications:
- Navigation: Pilots and sailors often use Pythagorean Triples to navigate distances across a two-dimensional plane.
- Construction: Pythagorean Triples are crucial in ensuring that corners are square in building projects.
- Computer Graphics: These triples help in generating geometric figures, solving distance problems in virtual environments.
Pythagorean Triples are a testament to the elegance of mathematics, showing how simple equations can yield a plethora of number combinations. Whether you're solving a puzzle or designing a building, the principles behind Pythagorean Triples enrich your understanding of geometry and algebra.
By engaging with this worksheet and exploring these methods, you'll not only solve mathematical problems but also appreciate the symmetry and order found in numbers. Remember, the journey through Pythagorean Triples is both educational and enjoyable, unveiling patterns that have fascinated minds for millennia.
What is the significance of Pythagorean Triples in mathematics?

+
Pythagorean Triples are important in mathematics as they provide a tangible representation of the Pythagorean Theorem, helping to understand and apply geometry, number theory, and algebra. They are used to verify the right angles in triangles and have applications in various fields.
How can students benefit from working with Pythagorean Triples?

+
Working with Pythagorean Triples helps students develop number sense, logical thinking, and problem-solving skills. It also introduces them to concepts in algebra and geometric proofs, making abstract mathematics more accessible and understandable.
Are there methods to find all Pythagorean Triples?

+
While there are formulas like Euler’s to generate an infinite number of Pythagorean Triples, finding all possible triples would require considering every pair of (m) and (n) values, which is practically infinite. However, we can generate an exhaustive list for any finite set of (m) and (n).