5 Key Tips for Pythagorean Theorem Word Problems

In today's mathematics lesson, we delve into the realm of Pythagorean theorem word problems. These problems are not only fundamental in understanding the relationship between the sides of a right-angled triangle but are also a staple in many standardized tests, mathematical curricula, and real-world applications. Here, we'll explore the 5 key tips to excel in solving these problems, ensuring that students can confidently tackle any geometric challenge that comes their way.
1. Understand the Pythagorean Theorem

Before diving into word problems, it’s crucial to have a solid grasp of the Pythagorean Theorem itself. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of squares of the other two sides. Mathematically, this can be written as:
a² + b² = c²
- 'a' and 'b' represent the lengths of the legs of the triangle
- 'c' represents the length of the hypotenuse
2. Identify the Type of Problem

Pythagorean theorem problems can generally be categorized into two types:
- Finding the hypotenuse: You know the lengths of the two legs and need to find the hypotenuse.
- Finding one of the legs: You know the length of the hypotenuse and one leg; you need to find the other leg.
Recognizing the type of problem helps you set up the equation correctly:
- For finding the hypotenuse: c = √(a² + b²)
- For finding a leg: a = √(c² - b²)
3. Solve Word Problems Step-by-Step
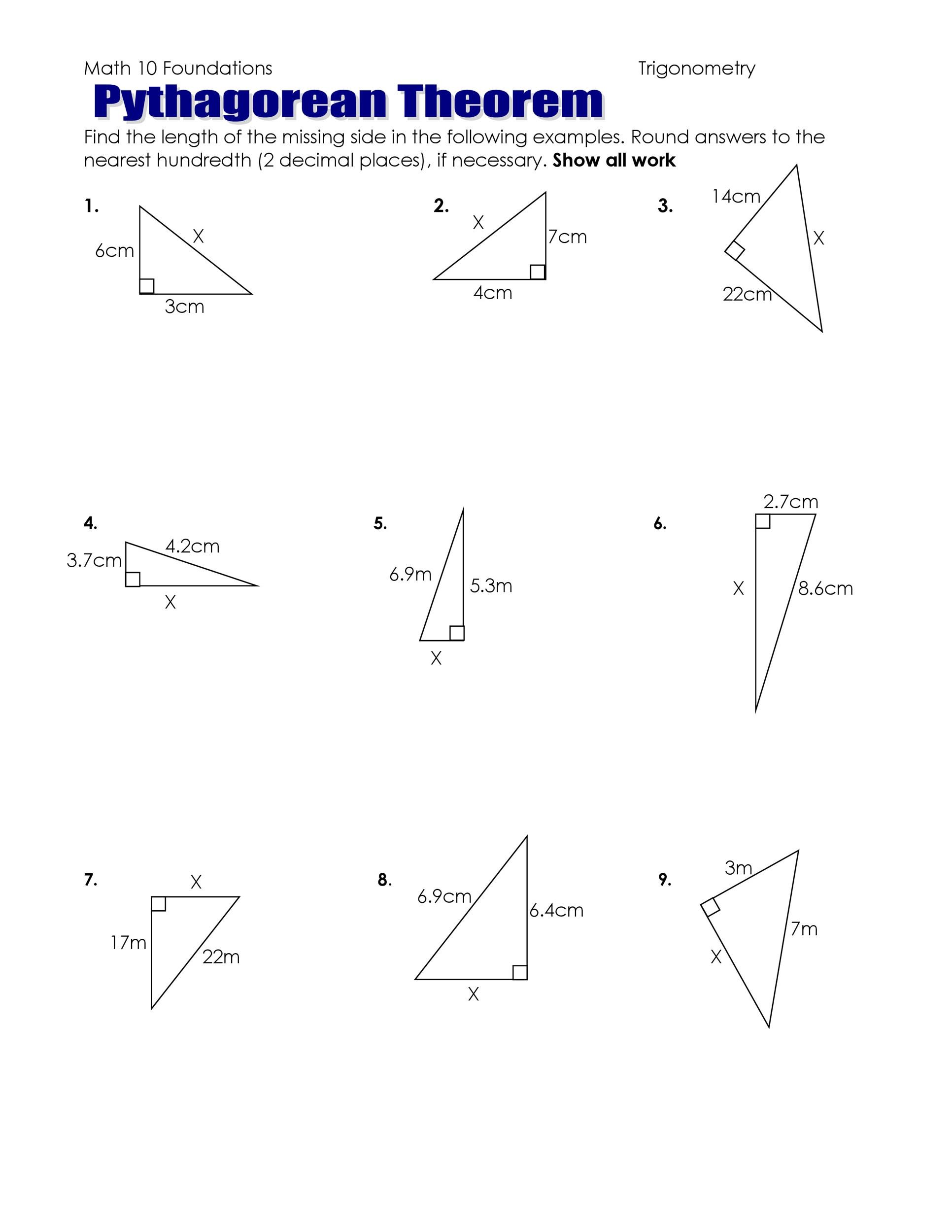
Here are the steps you should follow when solving word problems involving the Pythagorean Theorem:
- Draw a Diagram: Visualize the problem by drawing the triangle. Label the sides appropriately.
- Identify Given Information: Determine which sides are known and which need to be found.
- Set Up the Equation: Using the theorem, set up your equation. Substitute the known values.
- Calculate: Solve the equation for the unknown side. Remember to take the square root to get the actual length.
- Verify: If possible, check your answer by inserting it back into the equation to ensure the sides conform to the theorem.
4. Practical Application of the Theorem

Consider a real-world scenario:
A ladder leaning against a wall forms a right triangle with the wall and the ground. If the ladder is 10 meters long and the base of the ladder is 6 meters from the wall, how high does the ladder reach on the wall?
- Let's denote:
- The height of the wall = 'h' meters
- The length of the ladder = hypotenuse, 10 meters
- The base from the wall = one leg, 6 meters
Using the Pythagorean Theorem:
(10)² = (6)² + h²
100 = 36 + h²
h² = 100 - 36
h² = 64
h = √64
h = 8 meters
🎯 Note: Always ensure that your calculations reflect the real-world scenario accurately, as sometimes additional forces like friction or safety margins are not considered in theoretical problems.
5. Special Right Triangles

Recognize common special right triangles:
- 45°-45°-90° Triangle: In this triangle, the two legs are equal, and the hypotenuse is √2 times the length of each leg.
- 30°-60°-90° Triangle: Here, if the shortest side (opposite the 30° angle) is 'x', then the hypotenuse is 2x, and the side opposite the 60° angle is x√3.
Memorizing these properties can significantly speed up your problem-solving time.
Recapitulation

Pythagorean theorem word problems are more than just calculating the lengths of triangle sides; they are exercises in logical thinking, understanding relationships, and applying mathematical concepts to everyday scenarios. By mastering these tips, not only do you enhance your problem-solving skills, but you also gain a deeper appreciation for the structure and beauty of geometry. The ability to dissect a problem, understand its components, and apply the Pythagorean Theorem effectively can empower you in a variety of academic and practical situations.
How can you identify if a triangle is a right triangle?

+
A triangle is right if it has an angle of 90°. However, if you don’t have the angles, check if the Pythagorean Theorem holds true: a² + b² = c² for the sides you know.
Can the Pythagorean Theorem be used for any triangle?

+
The Pythagorean Theorem applies specifically to right triangles. However, with some additional trigonometry or geometric properties, you can extend its use to other triangles, but it’s not a straightforward application.
What are some real-life uses of the Pythagorean Theorem?

+
It’s widely used in construction to check the straightness of a wall or to determine distances, in navigation to calculate the shortest distance between two points, and in computer graphics for rendering 3D objects.