Pythagorean Theorem Word Problems Practice Worksheet

The Pythagorean Theorem is a cornerstone in the study of geometry, offering a straightforward yet powerful relationship between the sides of a right triangle. This theorem, often represented by the equation a^2 + b^2 = c^2, where a and b are the legs, and c is the hypotenuse, has practical applications in a variety of real-world scenarios. This blog post will guide you through the process of tackling word problems using the Pythagorean Theorem, providing both step-by-step explanations and practice problems to sharpen your skills.
Understanding the Pythagorean Theorem

The essence of the Pythagorean Theorem lies in understanding that in any right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Here's how you can conceptualize it:
- The legs: These are the two shorter sides of the triangle.
- The hypotenuse: This is always the longest side and forms the triangle's right angle.
The formula itself, a^2 + b^2 = c^2, helps in finding an unknown side of a right triangle when the lengths of the other two sides are known.
Steps to Solve Pythagorean Theorem Word Problems
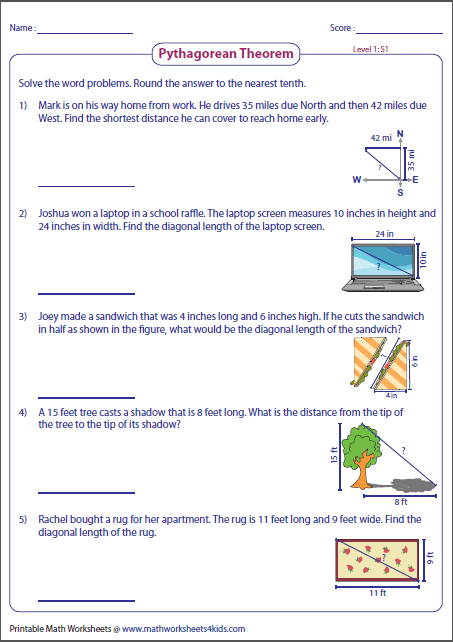
Here is a systematic approach to solving word problems with the Pythagorean Theorem:
- Read and Understand the Problem: Carefully read through the problem to understand what you are asked to find.
- Identify the Elements: Determine which sides are known and which you need to find.
- Sketch a Diagram: Visualize the problem by drawing a simple sketch. This often helps in seeing which sides correspond to a, b, and c.
- Set Up the Equation: Using the theorem, set up the equation where a^2 + b^2 = c^2.
- Solve for the Unknown: If solving for c, square both known sides, add them, then take the square root. If solving for a or b, subtract the square of the known side from the square of c and then take the square root.
- Check Your Work: Ensure the numbers make sense in the context of the problem. For example, the hypotenuse should always be longer than the legs.
- Express the Answer: Write your final answer in the form the question asks for, whether it's the length of a side or a statement about the triangle.
Example Problem

Suppose you're asked to find the height of a ladder that reaches 9 meters high when placed against a wall if the base of the ladder is 3 meters away from the wall.
Here's how you can solve this:
- Identify the Elements: The wall height (9 meters) is one leg, the distance from the wall to the ladder's base (3 meters) is the other leg. We need to find the hypotenuse, which is the ladder's length.
- Set Up the Equation: a^2 + b^2 = c^2 becomes 3^2 + 9^2 = c^2
- Solve for c: \[ c = \sqrt{3^2 + 9^2} = \sqrt{9 + 81} = \sqrt{90} \approx 9.487 \text{ meters} \]
- Check Your Work: The result seems logical as the ladder is longer than the wall's height.
📌 Note: Always remember to take the square root after solving for c^2 or a^2 or b^2.
Practice Worksheet

Here are some practice problems to help you master solving word problems with the Pythagorean Theorem:
| Problem | Calculation |
|---|---|
| A rectangle has a diagonal of 15 cm. If one side is 9 cm, find the length of the other side. | a^2 + 9^2 = 15^2 \rightarrow a = \sqrt{15^2 - 9^2} = 12 \text{ cm} |
| A ladder is placed 10 feet away from the wall and reaches 17 feet up the wall. How long is the ladder? | 10^2 + 17^2 = c^2 \rightarrow c = \sqrt{10^2 + 17^2} \approx 19.8 \text{ feet} |
| Find the length of a right triangle's third side if one leg is 5 cm and the other is 12 cm. | 5^2 + 12^2 = c^2 \rightarrow c = \sqrt{5^2 + 12^2} \approx 13 \text{ cm} |

The practice worksheet above provides a structured way to apply the Pythagorean Theorem, ensuring you understand how to derive each side of the triangle from known information.
What is the Pythagorean Theorem?

+
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). The formula is a^2 + b^2 = c^2.
How do I solve for a side in a right triangle?

+
If you know two sides, you can solve for the third side using the Pythagorean Theorem. If you need to find c, use c = \sqrt{a^2 + b^2}. If you need to find one leg, use a = \sqrt{c^2 - b^2} or b = \sqrt{c^2 - a^2}.
Are there any real-world applications of the Pythagorean Theorem?
+
Yes, it's used in construction to ensure buildings are level, in navigation to calculate distances, in video games for pathfinding algorithms, and in many other fields where right angles are involved.
Can the Pythagorean Theorem be used on non-right triangles?

+
The Pythagorean Theorem specifically applies to right triangles. For non-right triangles, you use the Law of Cosines, which includes the angles of the triangle.
🚀 Note: Use these practice problems to hone your skills, and remember, understanding the Pythagorean Theorem opens up a wide range of applications in both theoretical and practical settings.
This blog post has demonstrated how to apply the Pythagorean Theorem to solve word problems, ensuring that the steps and techniques can be used consistently to find unknown sides in various geometric scenarios. Whether you’re studying for an exam or applying geometry in real-life situations, the theorem remains an invaluable tool in your mathematical toolkit.