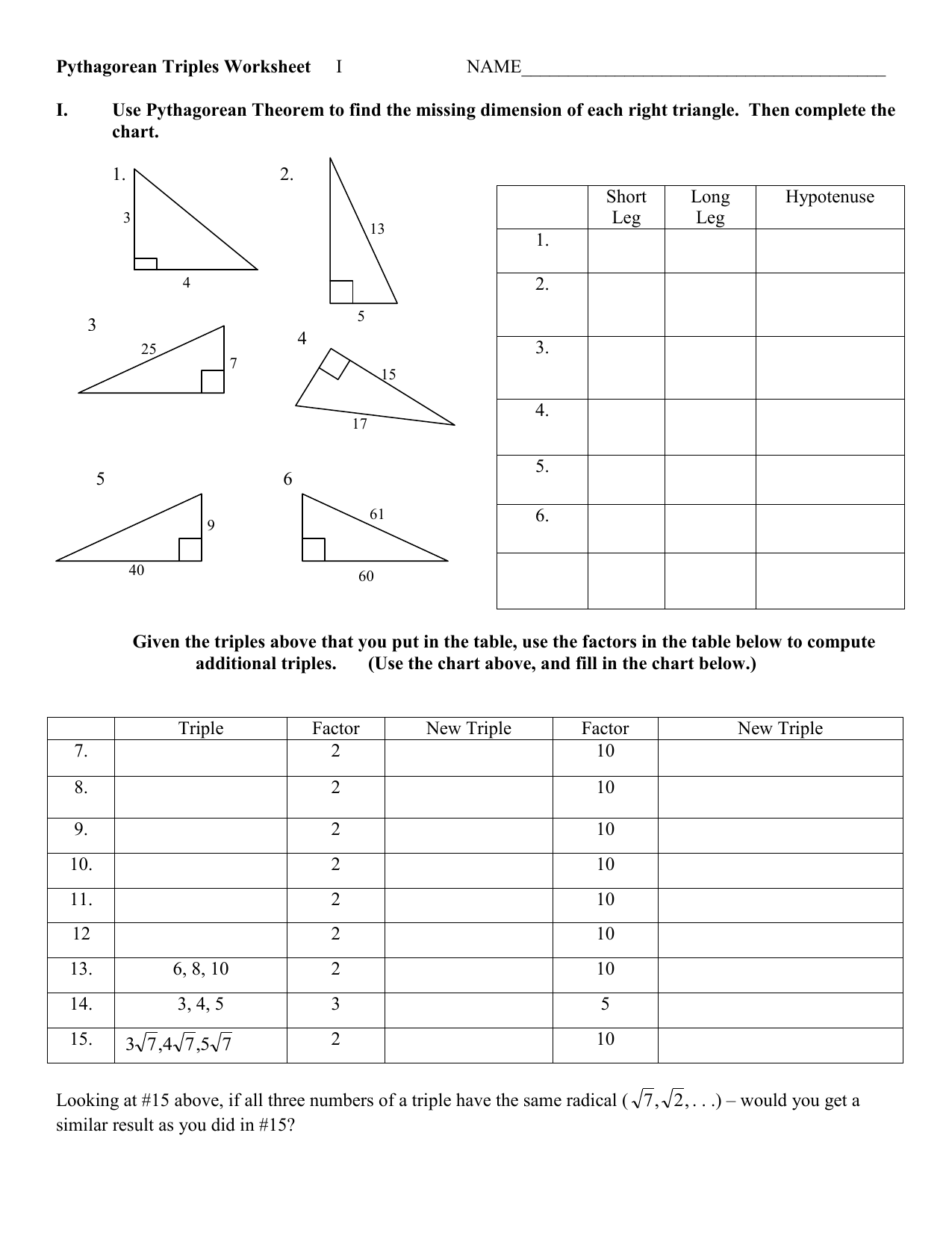
5 Proven Tips for Mastering Pythagorean Triples Worksheets
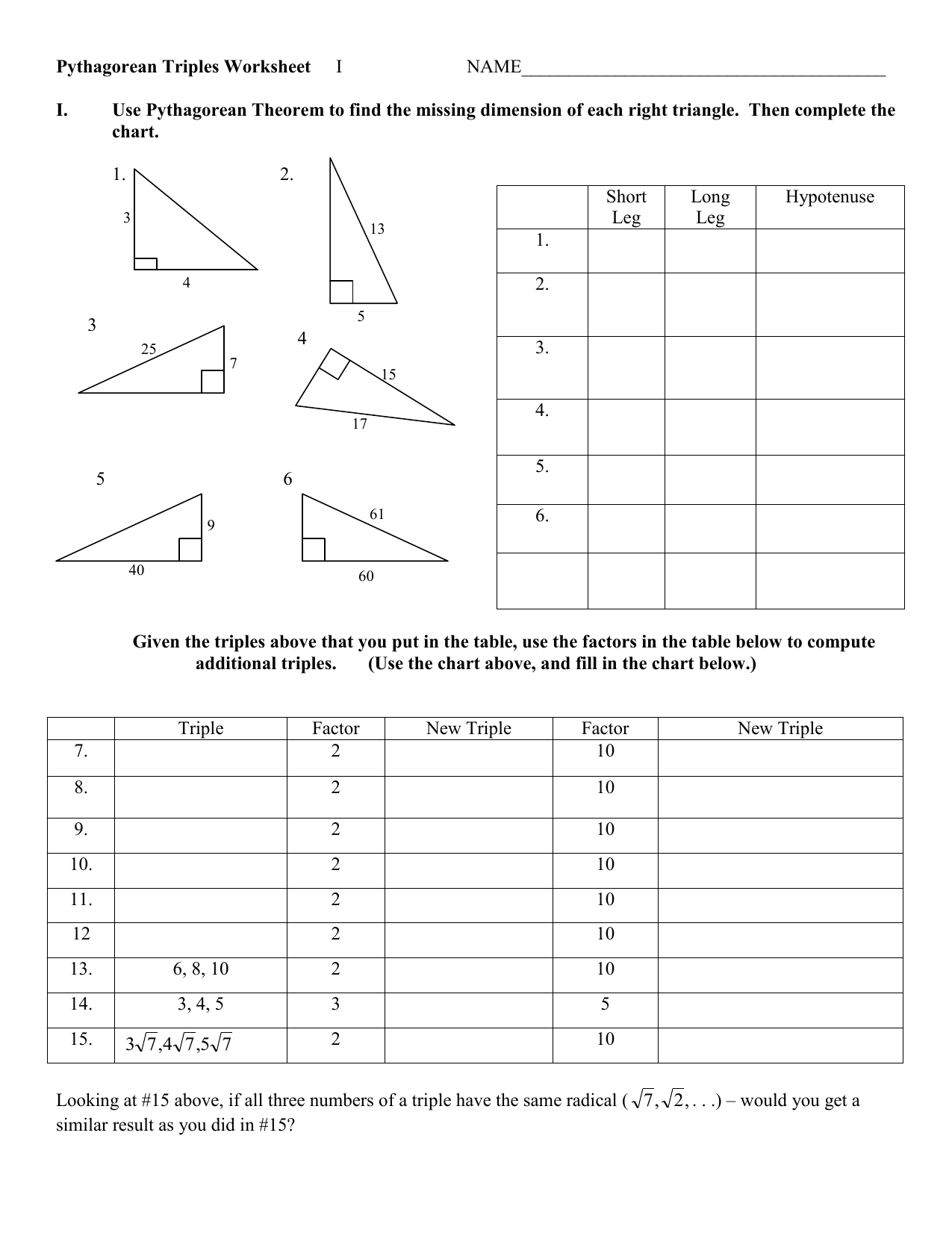
In the realm of mathematics, especially within the field of geometry and algebra, understanding Pythagorean triples is fundamental for a student's mathematical growth. These sets of three integers, where the square of one is the sum of the squares of the other two, form the backbone of many geometric calculations. Whether you're a student aiming to sharpen your math skills or an educator looking for effective teaching strategies, mastering Pythagorean triples can significantly elevate your mathematical proficiency. Here are five proven tips to help you excel in this fascinating mathematical concept through the use of Pythagorean Triples Worksheets:
Understanding the Basics

Before diving into complex problems, it's crucial to understand what Pythagorean triples are:
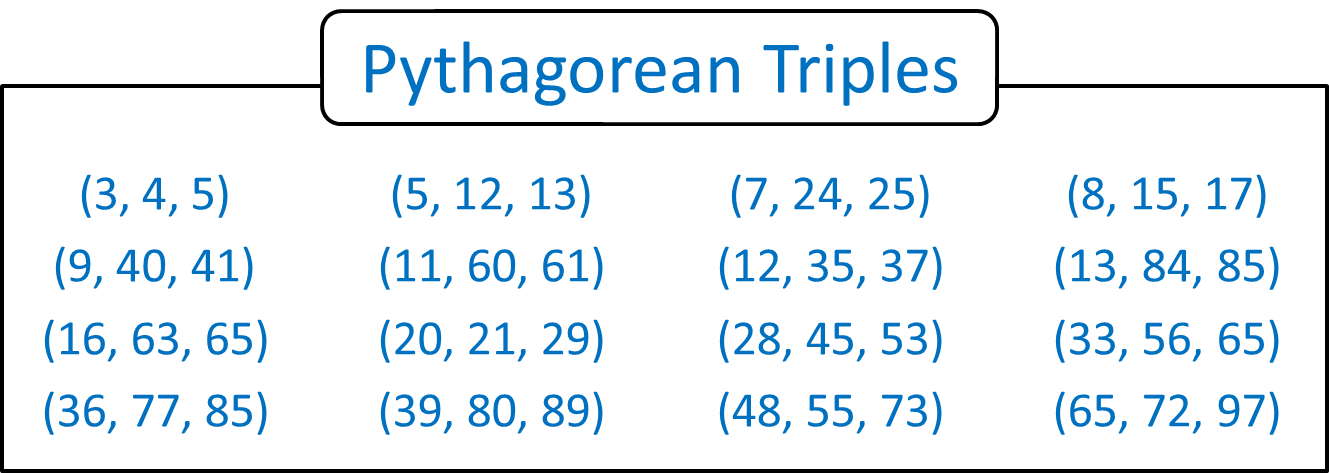
- A Pythagorean triple consists of three positive integers (a, b, c) such that a² + b² = c².
- Examples include (3, 4, 5), (5, 12, 13), and (8, 15, 17).
💡 Note: Pythagorean triples can be primitive (no common divisors among a, b, and c except for 1) or non-primitive.
1. Start with Simple Examples

Worksheets should begin with basic, well-known Pythagorean triples:
- Start by providing examples like (3, 4, 5) and ask students to verify the relationship through calculations.
- Use these simple examples to illustrate how the theorem works in practical scenarios, perhaps in a right triangle or real-world applications.
🧮 Note: Make sure to explain that multiplication of a Pythagorean triple by any positive integer also results in a valid Pythagorean triple.
2. Utilize Visualization Tools

Visualization is a powerful tool in math education:
- Include diagrams or geometric models on worksheets that illustrate how Pythagorean triples fit into right triangles.
- Use color-coding or different shapes to differentiate between the two shorter sides (a and b) and the hypotenuse (c).
| a | b | c | Visual |
|---|---|---|---|
| 3 | 4 | 5 | Image of a 3-4-5 triangle |

🎨 Note: Visual aids can help students grasp how the area of squares formed by the sides of the triangle correspond to the theorem.
3. Progressively Increase Complexity

As students become familiar with the basics, worksheets should:
- Introduce more complex triples that involve larger numbers or require more calculations to verify.
- Challenge students to find triples from given side lengths.
- Offer exercises where students have to generate their own triples or use formulas like a = m² - n², b = 2mn, c = m² + n².
📈 Note: Gradually increasing complexity helps in building mathematical confidence and problem-solving skills.
4. Engage with Real-Life Applications
Relating math to everyday scenarios:
- Develop worksheets with real-life applications where understanding Pythagorean triples is beneficial, like in construction, navigation, or game design.
- Include scenarios that require calculating the length of a ladder needed to reach a certain height on a wall.
🌉 Note: Showcasing real-life uses can make abstract math concepts more relatable and engaging.
5. Incorporate Interactive Elements

Worksheets should not just be a list of problems but should engage students:
- Include puzzles where students solve for missing sides or complete partial triples.
- Encourage the use of technology like Pythagorean triples generators or calculators to explore and verify triples.
- Create activities like treasure hunts where coordinates of the treasure rely on Pythagorean triples.
🔍 Note: Interactive elements can make learning dynamic, encouraging students to explore and apply the theorem in various contexts.
In conclusion, mastering Pythagorean triples can open the door to a deeper understanding of geometry, enhance problem-solving abilities, and provide practical skills in various fields. By employing these strategies, educators can foster an environment where students not only grasp the mathematical concepts but also enjoy the learning process. Through a systematic approach using worksheets tailored to various skill levels and real-life applications, students can confidently navigate the world of Pythagorean triples, setting a strong foundation for further mathematical exploration.
What is the purpose of learning about Pythagorean triples?
+
Learning about Pythagorean triples helps students understand the relationship between the sides of a right triangle, which is fundamental in geometry. This understanding can extend to various practical applications like construction, computer graphics, and physics.
Can Pythagorean triples be negative?

+
No, Pythagorean triples consist of three positive integers. Negative or zero values do not form valid triples according to the theorem.
How are Pythagorean triples used in video games?

+
In video games, Pythagorean triples can be used for pathfinding, calculating distances, or creating game environments where right angles are involved, like in first-person shooters or puzzles where characters need to move in a grid or solve geometric problems.