Pythagorean Theorem Worksheet: Engage with Interactive Learning!

Delving into the Pythagorean Theorem is not just a typical mathematical journey; it’s an exploration into one of the oldest and most fundamental principles in geometry. Dating back to over 2500 years, this theorem named after the ancient Greek mathematician, Pythagoras, has fascinated scholars, students, and enthusiasts alike. It elegantly connects the sides of a right triangle in a simple yet powerful relationship: if a and b are the lengths of the triangle's legs, and c is the length of the hypotenuse, then a2 + b2 = c2. But how can this timeless formula become an engaging tool for learning? This blog post aims to walk you through an interactive worksheet designed to make the Pythagorean Theorem not just understandable, but truly enjoyable to learn.
What is the Pythagorean Theorem?

At its core, the Pythagorean Theorem provides a way to calculate the length of any side of a right triangle when the lengths of the other two sides are known. Here’s a brief look at its essence:
- Right Triangle: A triangle with one angle measuring 90 degrees.
- Legs (a and b): The two shorter sides that form the right angle.
- Hypotenuse ©: The longest side opposite the right angle.
🔍 Note: While Pythagoras is often credited, this theorem was known in various cultures before him, including ancient Indian and Chinese mathematics.
The Interactive Pythagorean Theorem Worksheet

Here’s a detailed look at how you can engage with the Pythagorean Theorem through interactive learning:
Step-by-Step Interactive Exercises

The worksheet starts with simple exercises and gradually increases in complexity:
- Basic Application: Calculate the hypotenuse of a right triangle with given legs.
- Inverse Problem: Given the hypotenuse and one leg, find the other leg.
- Multi-Step Problems: Include real-world scenarios where additional calculations are needed before applying the theorem.
Visual Aids and Interactive Elements
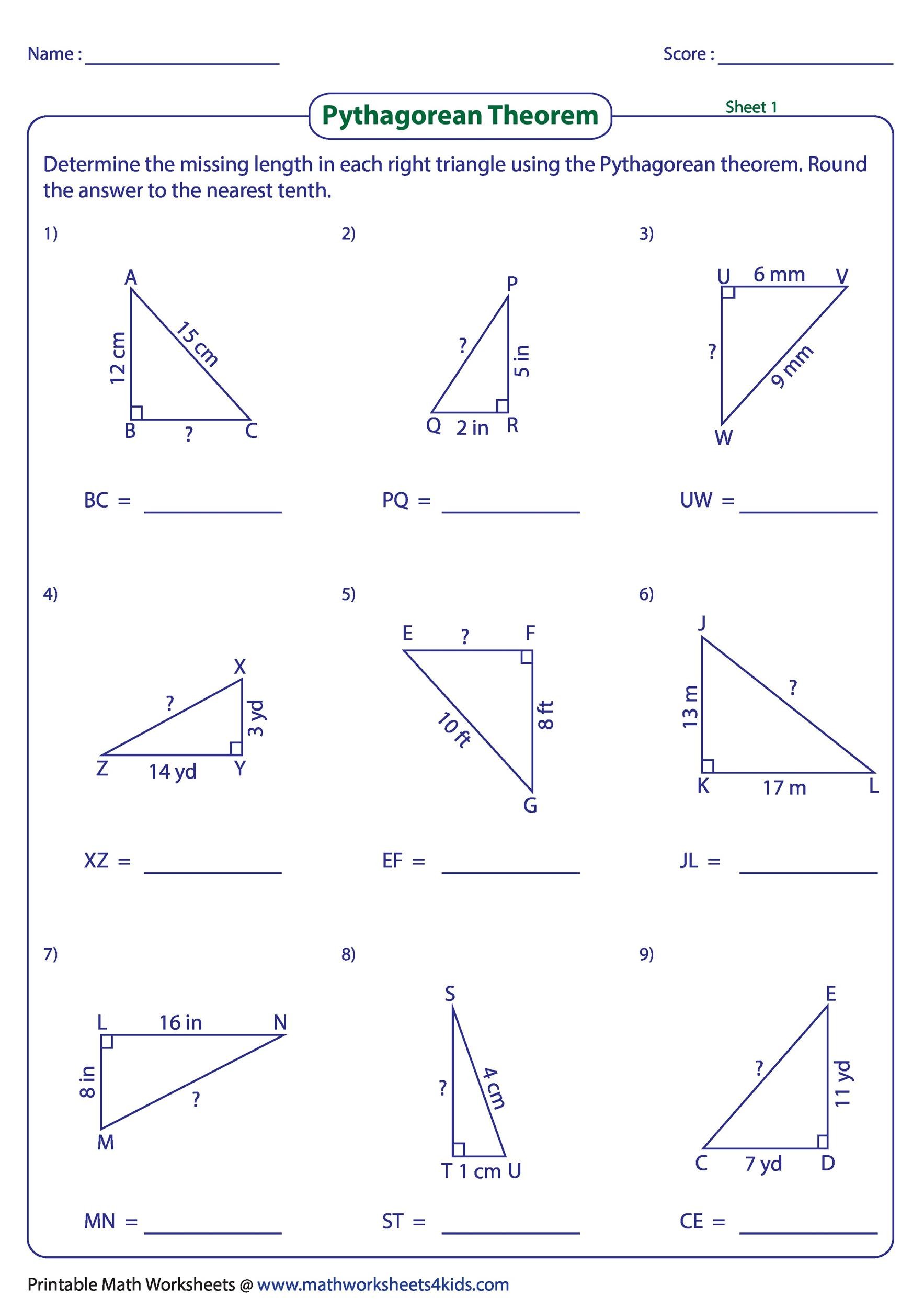
Visual learning aids:
- An interactive triangle grid where users can drag points to change the triangle’s dimensions and see how the theorem works dynamically.
- Sliders for adjusting the lengths of the sides to watch the formula’s outcomes in real-time.
- Images and animations showing historical contexts or cultural applications of the theorem.
| Visual Aid | Interactive Features |
|---|---|
| Triangle Grid | Drag to change sides |
| Sliders | Adjust sides length |
| Animations | Show historical uses |

Challenges and Puzzles

Here are some types of puzzles included in the worksheet:
- Puzzle Problems: Form triangles from given segments or solve visual puzzles.
- Proofs: Construct proofs of the theorem with visual or interactive elements.
- Estimation Challenges: Guess the length of the third side and then use the theorem to check accuracy.
Incorporating Multiple Disciplines
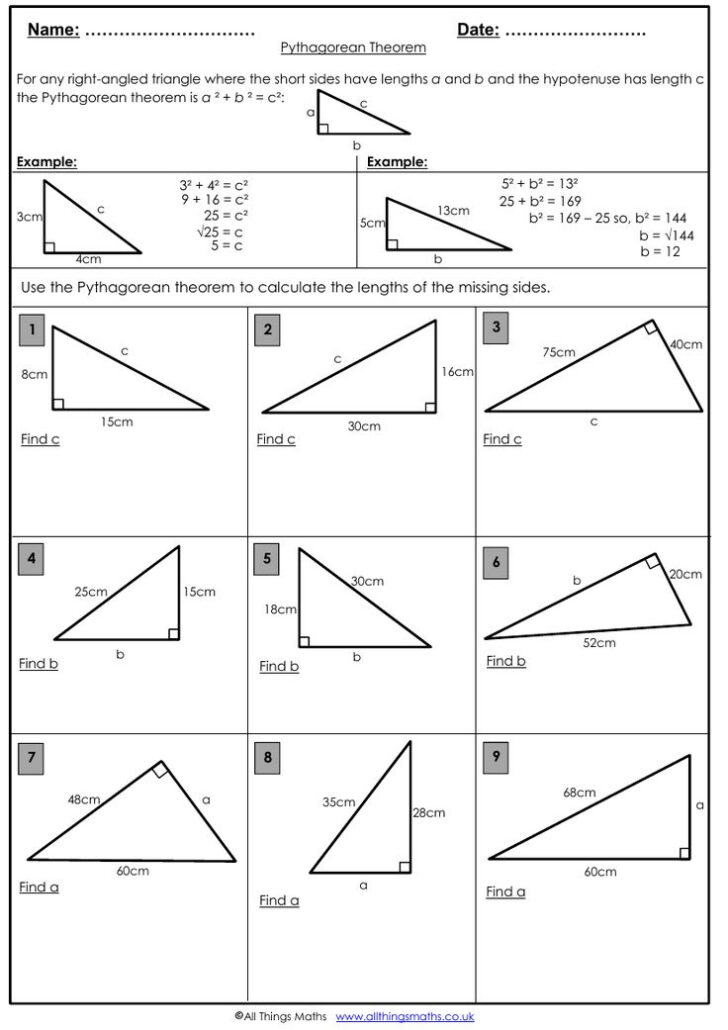
The Pythagorean Theorem’s applications are vast:
- Architecture: Understanding and applying the theorem in building design.
- Physics: Calculating resultant vectors or determining distances.
- Art: Creating geometric patterns or understanding perspective.
💡 Note: Integrating real-world applications not only makes learning engaging but also shows the relevance of mathematics in our daily lives.
In wrapping up our exploration of the Pythagorean Theorem through an interactive worksheet, we've seen how this ancient knowledge can be transformed into a modern, engaging learning tool. By incorporating visual aids, interactive elements, real-world applications, and challenging puzzles, the theorem becomes more than just a formula; it becomes a living, dynamic principle that students can interact with, understand, and remember. This approach not only demystifies the Pythagorean Theorem but also fosters a deeper appreciation for mathematics, turning passive learning into an active, thought-provoking journey. By engaging with the theorem through various interactive exercises, learners not only grasp the mathematical concept but also develop problem-solving skills, spatial awareness, and an appreciation for the historical and cultural significance of this fundamental geometric relationship.
Why is the Pythagorean Theorem important?

+
The Pythagorean Theorem is foundational in mathematics as it serves as a gateway to understanding distances and shapes in Euclidean space, impacting fields like architecture, navigation, and engineering.
Can the Pythagorean Theorem be proved interactively?

+
Yes, through visual proofs like the one where four congruent triangles are arranged to form a larger square, demonstrating the theorem’s validity.
How can interactive learning change my understanding of math?
+
Interactive learning engages multiple senses, making abstract concepts tangible and fostering deeper comprehension, motivation, and long-term retention.