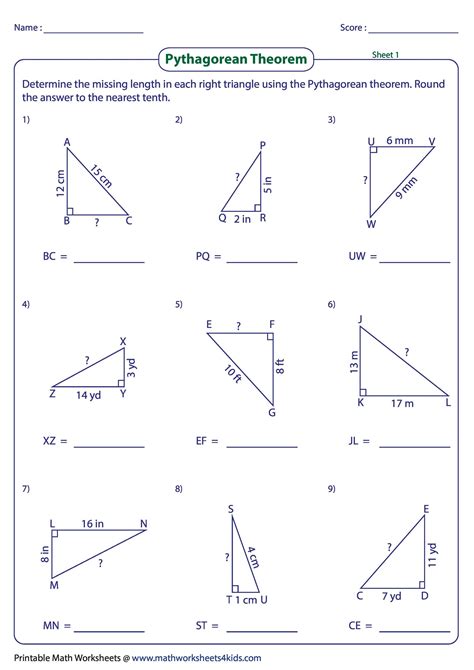
5 Proven Steps to Master the Pythagorean Theorem Converse

Understanding geometry becomes a lot more manageable once you grasp the fundamental concepts, and the Pythagorean Theorem converse is a crucial part of that. Not only does it enhance your problem-solving skills in geometry, but it also opens doors to applications in fields like engineering, architecture, and physics. Here's a detailed guide on how you can master this theorem effectively:
Step 1: Comprehend the Pythagorean Theorem

Before you delve into the converse of the theorem, make sure you understand the Pythagorean Theorem itself:
- The theorem states: In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of squares of the lengths of the other two sides.
- This can be mathematically expressed as ( c^2 = a^2 + b^2 ), where ( c ) is the hypotenuse, and ( a ) and ( b ) are the other two sides.

Step 2: Learn the Converse Theorem

The converse theorem of the Pythagorean Theorem reverses the condition:
- If the square of the length of one side of a triangle is equal to the sum of squares of the other two sides, then the triangle is a right triangle.
- This can be written as ( c^2 = a^2 + b^2 ) when applied to any triangle.
Here’s where you start practicing:
- Select a triangle where you’re not certain if it’s a right triangle.
- Calculate the squares of the sides.
- Use the converse theorem to verify if it’s a right triangle.

Step 3: Practice with Different Triangle Types

The converse theorem applies not just to triangles with obvious right angles:
- Try it on obtuse triangles where one angle is greater than 90°.
- Also, experiment with acute triangles where all angles are less than 90°.
📝 Note: This practice helps solidify your understanding by contrasting various scenarios where the theorem might or might not apply.
| Triangle Type | Condition |
|---|---|
| Right Triangle | c^2 = a^2 + b^2 |
| Obtuse Triangle | c^2 > a^2 + b^2 |
| Acute Triangle | c^2 < a^2 + b^2 |

Step 4: Solve Real-Life Problems
Apply the converse theorem to real-life scenarios:
- Estimating the height of a building or a tree by using shadows.
- Determining if a bridge is structurally sound based on its foundation.
Step 5: Use Visual and Conceptual Aids

Enhance your understanding with visual tools:
- Create models or use software to visualize the theorem and its converse.
- Watch educational videos or animations that illustrate the theorem in action.

As you've navigated through these five steps, you've not only learned the converse of the Pythagorean Theorem but also applied it in various contexts. This journey through mathematical theory to practical application underscores how mathematics can be both abstract and immensely practical. With the foundation laid out here, you're now equipped to tackle more complex geometric problems, delve deeper into trigonometry, or apply this knowledge to real-world engineering challenges. The beauty of the Pythagorean Theorem converse lies in its simplicity and the extensive reach of its applications, making it an indispensable tool in your mathematical toolkit.
What’s the difference between the Pythagorean Theorem and its converse?

+
The Pythagorean Theorem asserts that in a right triangle, ( c^2 = a^2 + b^2 ). Its converse, however, uses this same equation to determine if a triangle is a right triangle.
How do I know if a triangle is a right triangle?

+
Apply the Pythagorean Theorem’s converse: If the square of one side is equal to the sum of the squares of the other two sides, then it’s a right triangle.
Can the Pythagorean Theorem be applied to other polygons?
+
While the Pythagorean Theorem specifically applies to triangles, especially right triangles, concepts like the Law of Cosines generalize similar principles to any triangle.
What if I get ( c^2 \neq a^2 + b^2 ) in my calculation?

+
If ( c^2 \neq a^2 + b^2 ), the triangle is not a right triangle. Further, ( c^2 > a^2 + b^2 ) indicates an obtuse triangle, and ( c^2 < a^2 + b^2 ) indicates an acute triangle.
Why should I learn the Pythagorean Theorem converse?

+
The converse expands your ability to classify and analyze triangles, providing a deeper understanding of geometric relationships, which is essential in various scientific and technical fields.



