Pythagorean Theorem Worksheet
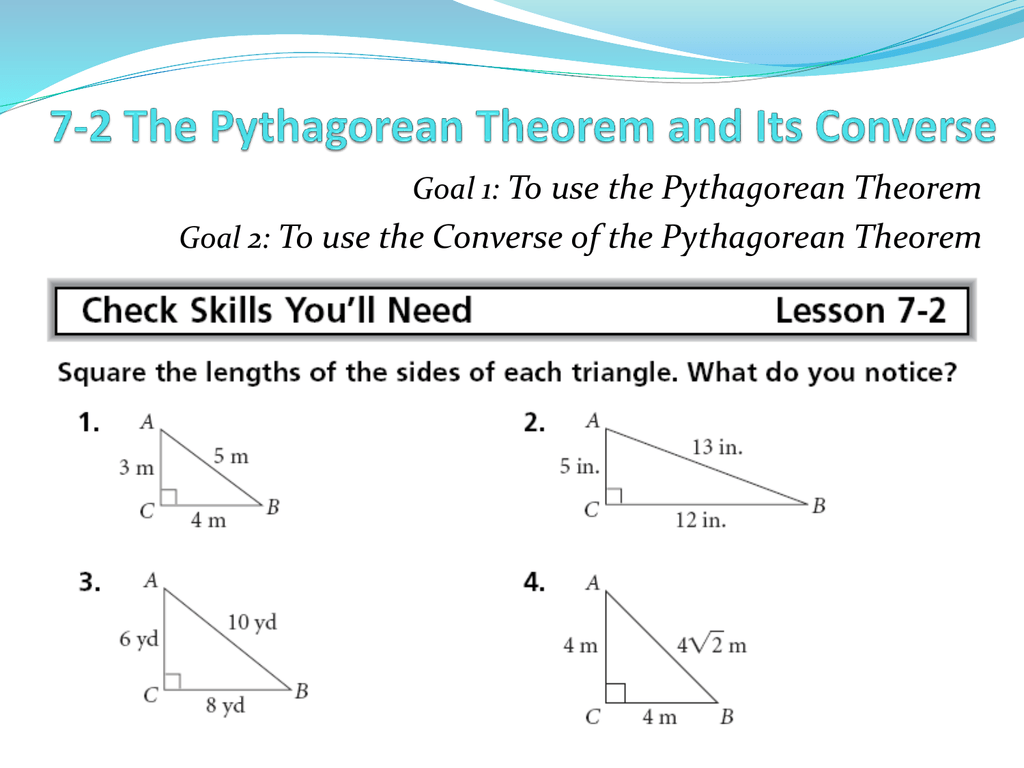
Introduction to the Pythagorean Theorem
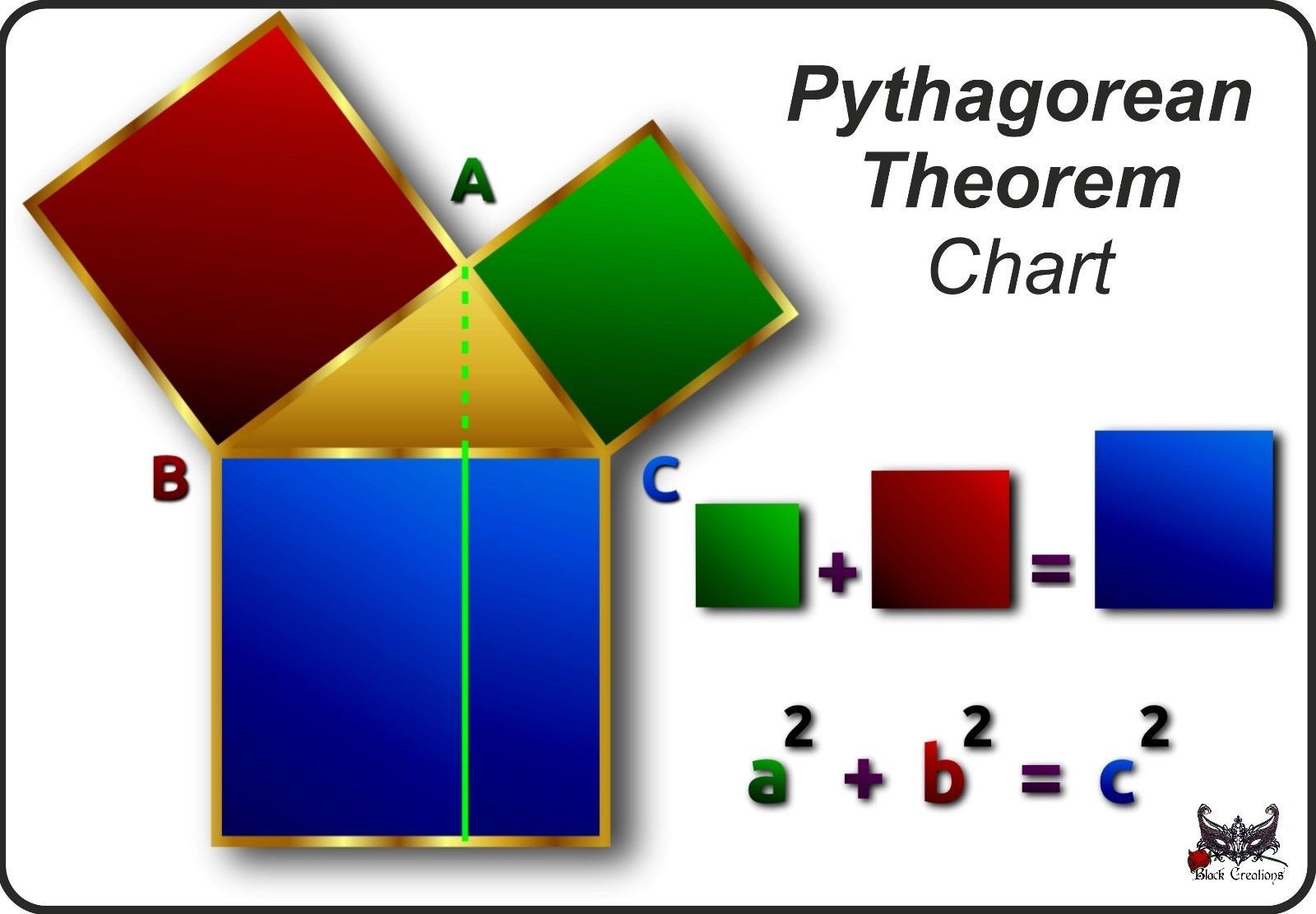
The Pythagorean Theorem is a fundamental concept in geometry, which describes the relationship between the lengths of the sides of a right-angled triangle. The theorem states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as a^2 + b^2 = c^2, where a and b are the lengths of the two sides, and c is the length of the hypotenuse.
Understanding the Pythagorean Theorem Formula
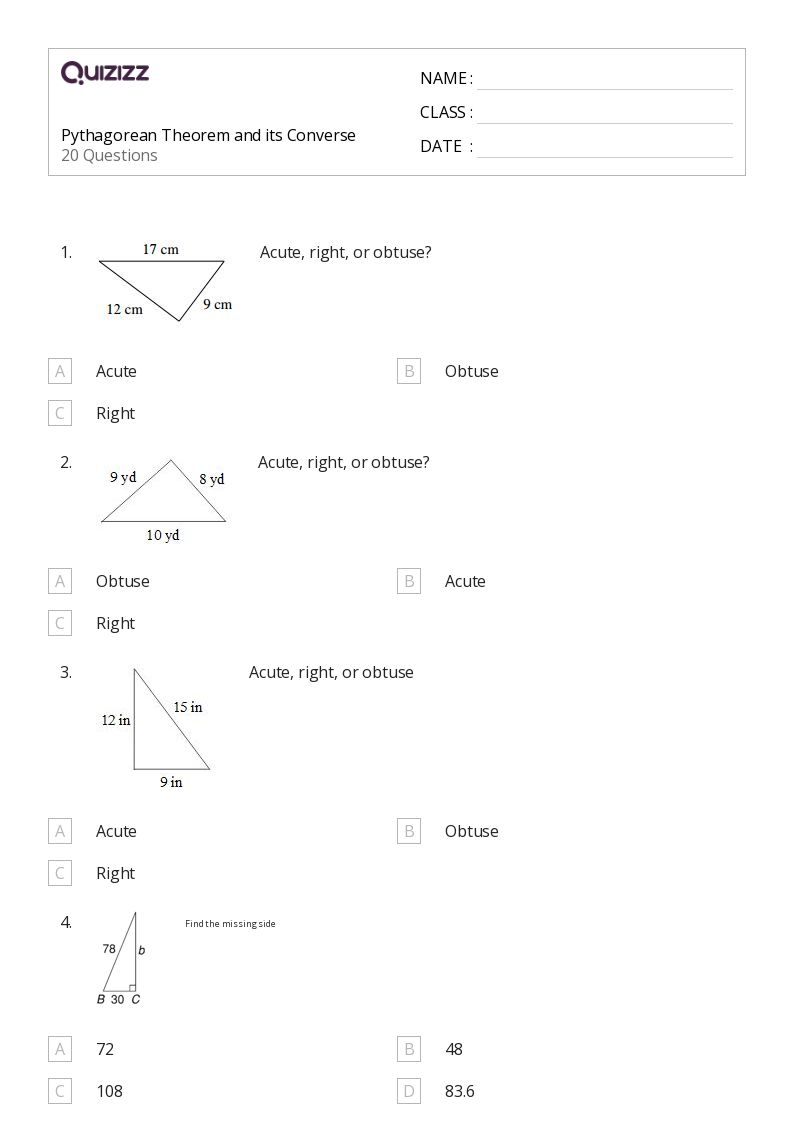
The formula a^2 + b^2 = c^2 is used to find the length of the hypotenuse of a right-angled triangle, given the lengths of the other two sides. For example, if the lengths of the two sides are 3 and 4, the length of the hypotenuse can be calculated as follows: c^2 = 3^2 + 4^2 c^2 = 9 + 16 c^2 = 25 c = √25 c = 5 Therefore, the length of the hypotenuse is 5.
Pythagorean Theorem Worksheet

Here are some examples of Pythagorean Theorem problems:
| Problem | Given Values | Solution |
|---|---|---|
| 1 | a = 5, b = 12 | c = √(5^2 + 12^2) = √(25 + 144) = √169 = 13 |
| 2 | a = 8, b = 15 | c = √(8^2 + 15^2) = √(64 + 225) = √289 = 17 |
| 3 | a = 20, c = 25 | b = √(c^2 - a^2) = √(25^2 - 20^2) = √(625 - 400) = √225 = 15 |
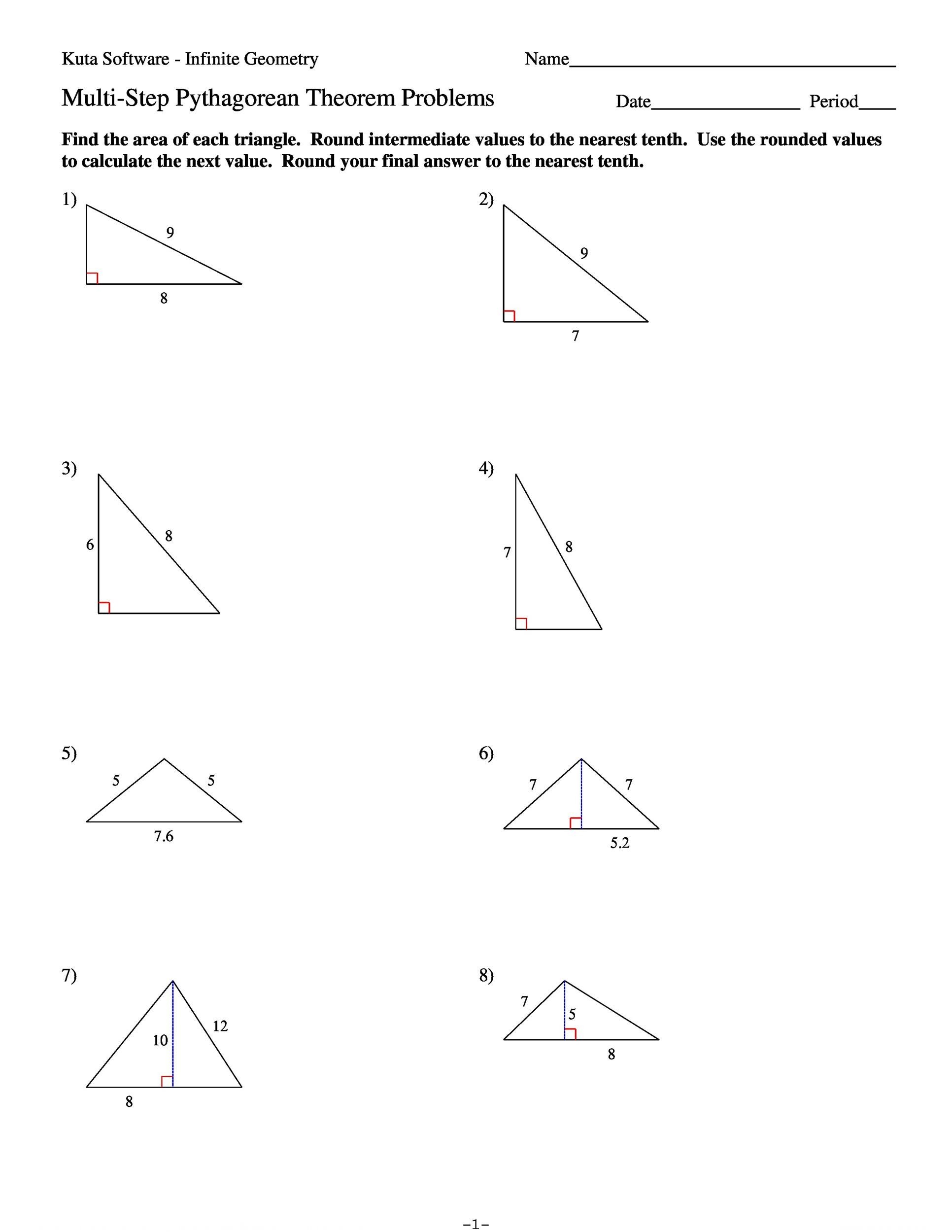
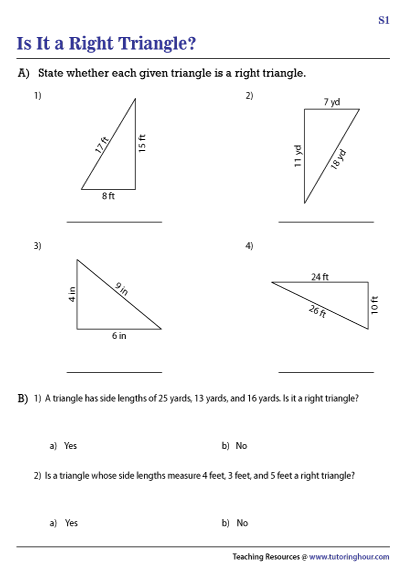
Practice Problems

Here are some practice problems to help you master the Pythagorean Theorem: * Find the length of the hypotenuse of a right-angled triangle with sides of length 6 and 8. * Find the length of the side of a right-angled triangle with a hypotenuse of length 10 and one side of length 6. * Find the length of the hypotenuse of a right-angled triangle with sides of length 9 and 12.
📝 Note: Make sure to use the correct formula and units when solving Pythagorean Theorem problems.
To solve these problems, simply plug in the given values into the Pythagorean Theorem formula and solve for the unknown value. For example, to find the length of the hypotenuse of a right-angled triangle with sides of length 6 and 8, you would use the formula: c^2 = 6^2 + 8^2 c^2 = 36 + 64 c^2 = 100 c = √100 c = 10 Therefore, the length of the hypotenuse is 10.
In summary, the Pythagorean Theorem is a powerful tool for finding the length of the hypotenuse of a right-angled triangle, given the lengths of the other two sides. By using the formula a^2 + b^2 = c^2, you can easily solve a wide range of problems involving right-angled triangles. With practice and patience, you can become proficient in using the Pythagorean Theorem to solve complex geometry problems.
What is the Pythagorean Theorem?
+
The Pythagorean Theorem is a mathematical formula that describes the relationship between the lengths of the sides of a right-angled triangle. It states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
How do I use the Pythagorean Theorem to find the length of the hypotenuse?

+
To find the length of the hypotenuse, simply plug in the given values into the Pythagorean Theorem formula and solve for the unknown value. For example, if the lengths of the two sides are 3 and 4, the length of the hypotenuse can be calculated as follows: c^2 = 3^2 + 4^2, c^2 = 9 + 16, c^2 = 25, c = √25, c = 5.
What are some common applications of the Pythagorean Theorem?

+
The Pythagorean Theorem has many practical applications in fields such as architecture, engineering, physics, and surveying. It can be used to find the length of the hypotenuse of a right-angled triangle, which is essential in designing and building structures, calculating distances and heights, and solving problems involving right-angled triangles.



