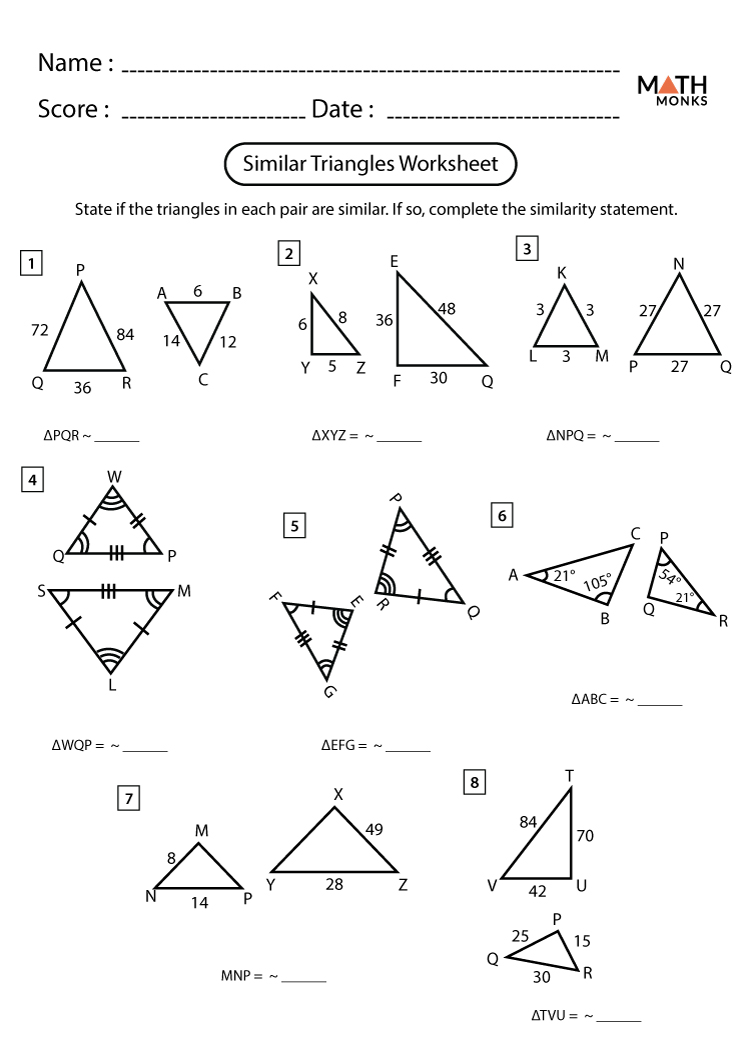
Prove Similar Triangles with Ease: Worksheet Guide

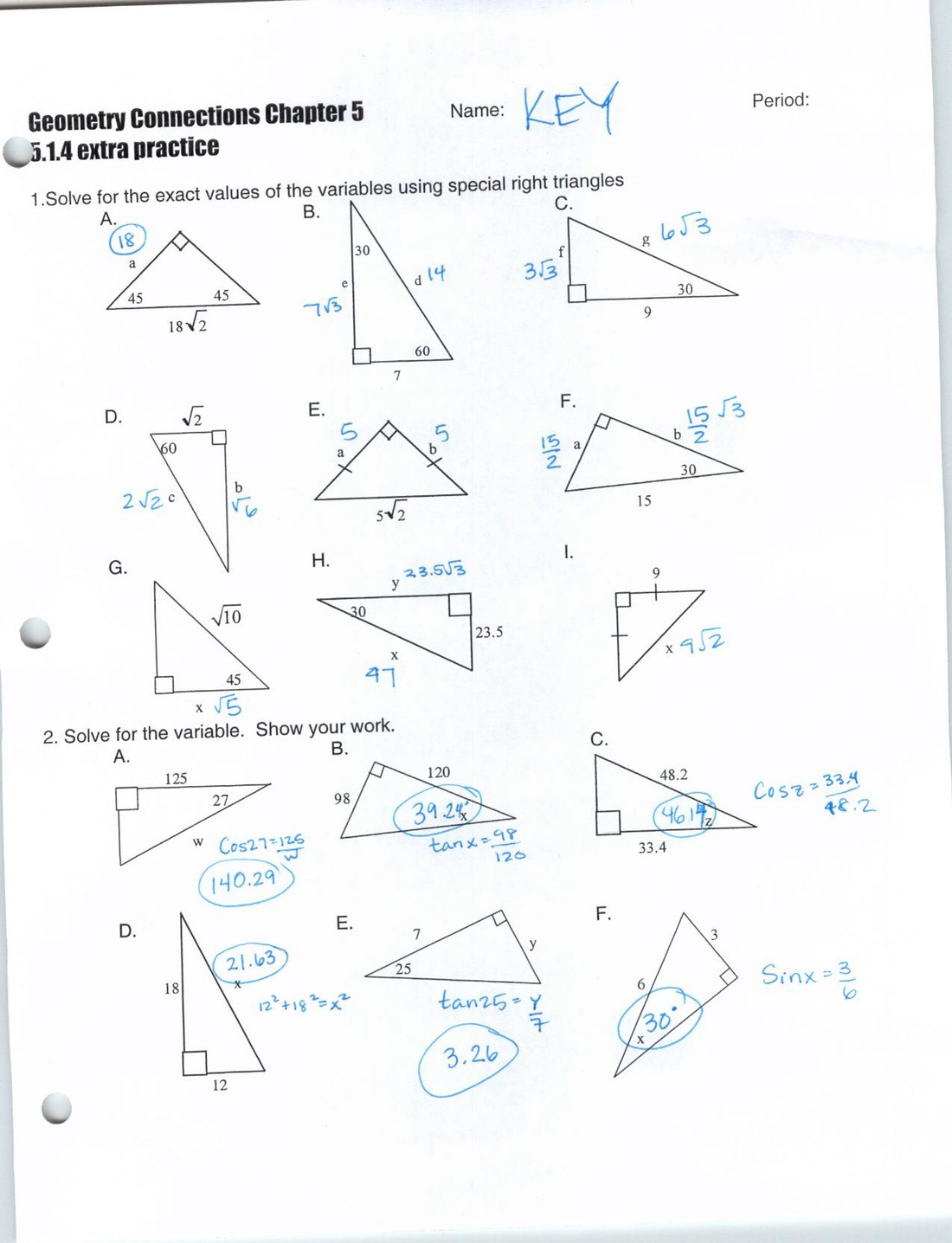
Exploring the fascinating world of geometry often involves delving into the nuances of triangles, one of the most studied shapes in mathematics due to their unique properties. Among these properties, proving triangles are similar stands out as a fundamental skill, crucial for various geometric applications and understanding spatial relationships. This long-form guide will take you through the different methods of proving triangle similarity, ensuring that you not only grasp the concept but also apply it effortlessly using a comprehensive worksheet guide.
Why Prove Similar Triangles?

Before we dive into the methods, let’s first understand why proving similarity between triangles is vital:
- Practical Applications: From architects drawing blueprints to engineers designing bridges, the concept of similarity underpins many real-world calculations where proportions must be preserved.
- Foundational Knowledge: Understanding how to prove similar triangles lays the groundwork for learning advanced geometry concepts.
- Mathematical Elegance: Proving similarity often involves elegant mathematical arguments that can enhance your appreciation for the beauty of geometry.
Essential Similarity Theorems

When proving that two triangles are similar, mathematicians rely on three key theorems:
- Angle-Angle (AA) Theorem: If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
- Side-Angle-Side (SAS) Theorem: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, the triangles are similar.
- Side-Side-Side (SSS) Theorem: If all three sides of one triangle are proportional to the corresponding sides of another triangle, they are similar.
Worksheet Guide for Proving Similarity

The following guide provides a step-by-step process to work through proving that triangles are similar using various problems. You can use this as a self-paced worksheet or with an instructor:
Exercise 1: AA Similarity

Given triangles with:
| Triangle ABC | Triangle DEF |
|---|---|
| ∠A = 60° | ∠D = 60° |
| ∠B = 45° | ∠E = 45° |
Prove triangles ABC and DEF are similar by AA theorem:
- Identify the angles given in both triangles.
- Check if any other pair of angles can be inferred as congruent (sum of angles in a triangle is 180°).
- Conclude using the AA theorem.
Exercise 2: SAS Similarity

Given triangles with:
| Triangle XYZ | Triangle UVW |
|---|---|
| XY/UW = 3⁄4 | YU/WX = 3⁄4 |
| ∠X = ∠U = 50° |
Prove triangles XYZ and UVW are similar by SAS theorem:
- Identify the proportional sides and the given congruent angles.
- Verify the included angles are indeed congruent.
- Use the SAS theorem to prove similarity.
Exercise 3: SSS Similarity

Given triangles with:
| Triangle JKL | Triangle MNO |
|---|---|
| J/K = M/N = 2⁄3 | K/L = N/O = 2⁄3 |
| L/J = O/M = 2⁄3 |
Prove triangles JKL and MNO are similar by SSS theorem:
- Identify the corresponding sides and their ratios.
- Confirm all sides are proportionally the same.
- Conclude using the SSS theorem.
🌟 Note: When using the SSS theorem, make sure you check the ratio for all three pairs of corresponding sides to ensure consistency.
Real-World Applications
Applying the concept of similar triangles in real-world scenarios not only makes the learning process more engaging but also demonstrates the practical value of this geometric theorem:
- Photography: When photographers aim to maintain proportions while zooming in or out, they rely on the principle of similarity.
- Map Making: Cartographers use similarity to accurately scale down large geographical areas onto maps.
- Computer Graphics: Algorithms for resizing, rendering, and texture mapping in computer graphics heavily depend on similarity.
To summarize, this guide has delved into the essential methods for proving triangle similarity, using a hands-on worksheet approach. By focusing on AA, SAS, and SSS theorems, you've learned how to identify, apply, and prove that triangles are indeed similar. Understanding these principles not only enhances your geometrical prowess but also has real-world applications across various fields. Remember, consistency in side ratios or congruent angles is key to successfully demonstrating triangle similarity. Keep practicing, and soon proving similar triangles will become second nature to you.
What is the difference between similar and congruent triangles?

+
Similar triangles have the same shape but may be different in size. Their angles are congruent, and their sides are proportional. On the other hand, congruent triangles are identical in both shape and size, with all corresponding sides and angles being equal.
Can two triangles be similar but not congruent?

+
Yes, triangles can be similar but not congruent if they have the same shape (congruent angles) but are of different sizes (proportional sides).
How do you know if two triangles are similar?

+
To know if two triangles are similar, you can use one of the similarity theorems: AA (Angle-Angle), SAS (Side-Angle-Side), or SSS (Side-Side-Side). If the conditions for any of these theorems are met, the triangles are similar.