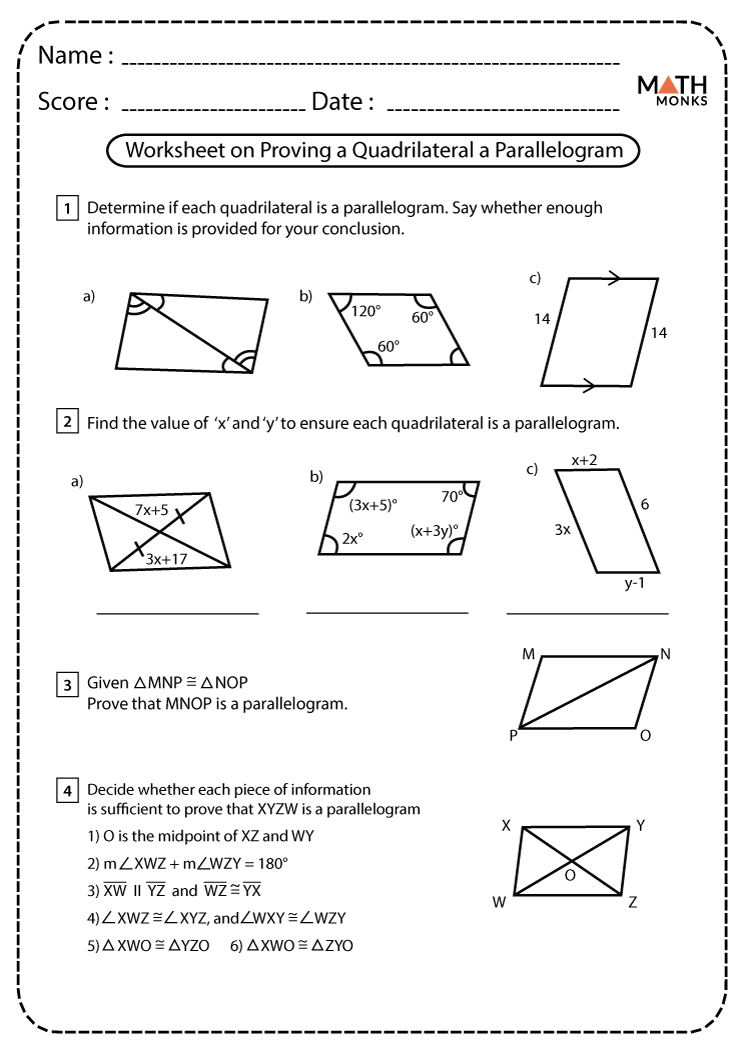
Prove Quadrilaterals Are Parallelograms: Free Worksheet
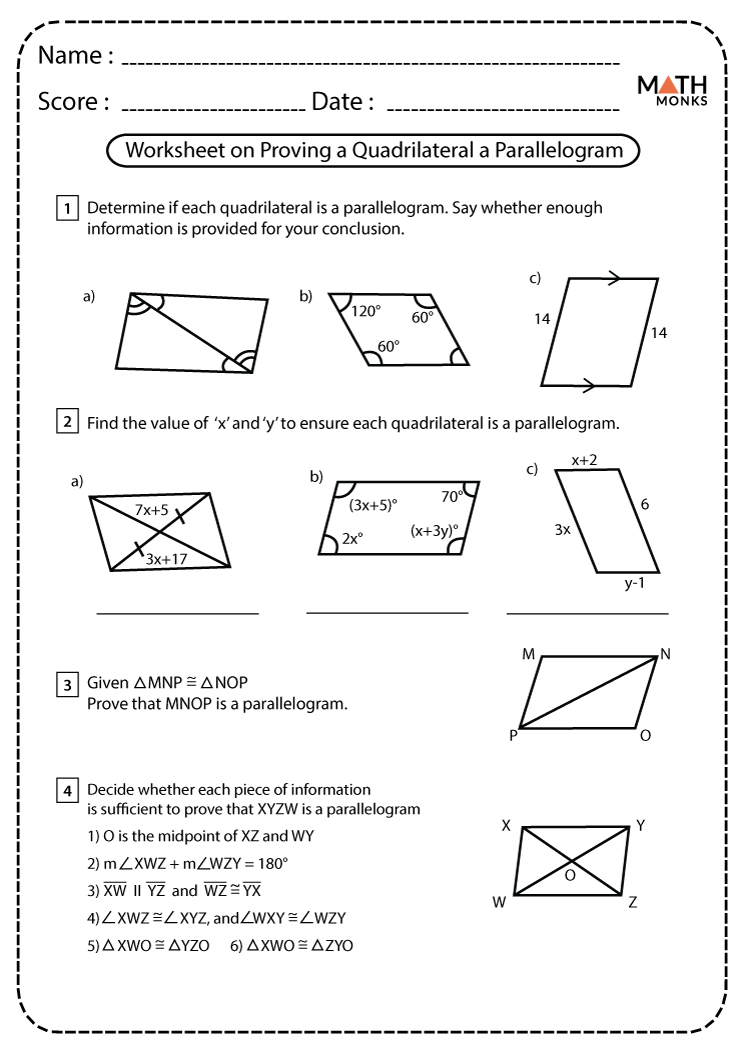
Geometry is not just about knowing the formulas but understanding the properties that connect various shapes. Among the most fundamental and intriguing shapes in geometry are quadrilaterals, especially when they take the form of parallelograms. This blog post delves into how we can prove that a quadrilateral is a parallelogram, offering insights and a practical free worksheet to assist you in mastering these proofs.
Understanding Parallelograms

A parallelogram is a quadrilateral where both pairs of opposite sides are parallel. Here are some of the core characteristics:
- Opposite sides are equal in length.
- Opposite angles are equal.
- Consecutive angles are supplementary.
- The diagonals bisect each other.
Understanding these properties helps in identifying and proving parallelograms.
Proving a Quadrilateral Is a Parallelogram

To prove that a given quadrilateral is indeed a parallelogram, several methods can be employed. Here are the most common ways:
1. Prove Both Pairs of Opposite Sides Are Parallel

If you can demonstrate that both sets of opposite sides are parallel, you have a parallelogram.
2. Prove Both Pairs of Opposite Sides Are Equal in Length

If all four sides are equal, the quadrilateral is a rhombus, which is a special case of a parallelogram.
3. Prove One Pair of Opposite Sides Are Both Parallel and Equal in Length
Just one pair of sides being equal and parallel is enough to show it's a parallelogram.
4. Prove Both Pairs of Opposite Angles Are Equal

Equal opposite angles ensure that the shape is a parallelogram.
5. Prove Diagonals Bisect Each Other

When the diagonals meet at their midpoints, the quadrilateral must be a parallelogram.
Step-by-Step Guide on Proving Parallelograms
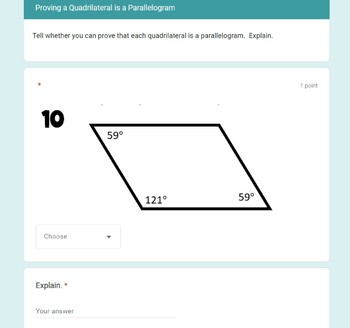
Step 1: Identify the Given Information

The first step in any proof is to list all the known information about the quadrilateral, which includes:
- Side lengths
- Angle measures
- Properties of lines (parallel, perpendicular)
- Diagonal characteristics
Step 2: Choose the Method of Proof

Based on the information available, select the most appropriate method from those listed above. Sometimes, more than one method can apply, but for simplicity, choose the method that involves the least steps.
Step 3: Set Up the Proof

Begin by stating what needs to be proved and then proceed with logical steps. Use the given properties and apply geometric theorems or postulates to deduce that the shape must be a parallelogram.
Step 4: Illustrate and Label

Use a diagram to visually represent your quadrilateral. Label all given measurements and draw lines to show parallel or equal sides or angles where necessary. This visual aid helps in understanding the relationships.
Step 5: Provide a Conclusion

Once the proof is established, clearly state the conclusion. Restate that the given quadrilateral is indeed a parallelogram based on the steps outlined.
Free Parallelogram Worksheet

To help you practice proving that a quadrilateral is a parallelogram, here’s a free worksheet:
| Given | Proof Method | Steps |
|---|---|---|
| AB = CD, AD || BC | One pair of opposite sides parallel and equal in length |
|
| AB || CD, AD || BC | Both pairs of opposite sides are parallel |
|
| AB = CD, AD = BC | Both pairs of opposite sides are equal |
|

📝 Note: Remember that the proof often involves combining more than one method or using additional geometric properties like triangle congruence or angle sum.
By practicing these examples, you can develop the skill of recognizing and proving parallelograms through various given conditions.
The ability to prove quadrilaterals as parallelograms is not only an essential skill for geometry but also enhances problem-solving abilities applicable in real-life scenarios like architecture, engineering, and design. Through understanding these proofs, one learns to appreciate the logical reasoning and the beauty of geometry where shapes tell a story of congruence and symmetry.
Can a trapezoid be a parallelogram?
+Yes, a trapezoid can be a parallelogram if it has one pair of opposite sides that are both parallel and equal in length. At this point, the trapezoid turns into a parallelogram since all four sides would now be parallel in pairs.
What is the difference between proving and assuming a quadrilateral is a parallelogram?
+Proving involves using given geometric properties to logically deduce that a shape is a parallelogram, while assuming a shape is a parallelogram uses its known properties to make other geometric calculations.
Why do we need to prove quadrilaterals are parallelograms?
+Proving shapes are parallelograms is fundamental in geometry because it allows us to leverage the properties of parallelograms to solve more complex problems involving areas, angles, and distances.
The beauty of geometry lies in its ability to connect logic with shapes, creating a dialogue between theory and practicality. Proving that a quadrilateral is a parallelogram is not just an academic exercise but a demonstration of how foundational principles can lead to undeniable truths in mathematics and beyond.