5 Clever Tricks to Prove Parallelograms Easily

Proving geometric shapes can be a complex puzzle, especially when it comes to parallelograms. A parallelogram, with its unique properties, often requires more than just a quick glance to confirm its identity. However, with a few clever tricks up your sleeve, proving that a quadrilateral is indeed a parallelogram can become much simpler and more intuitive. Here are five effective strategies to help you verify a parallelogram effortlessly.
The Opposite Angles Test
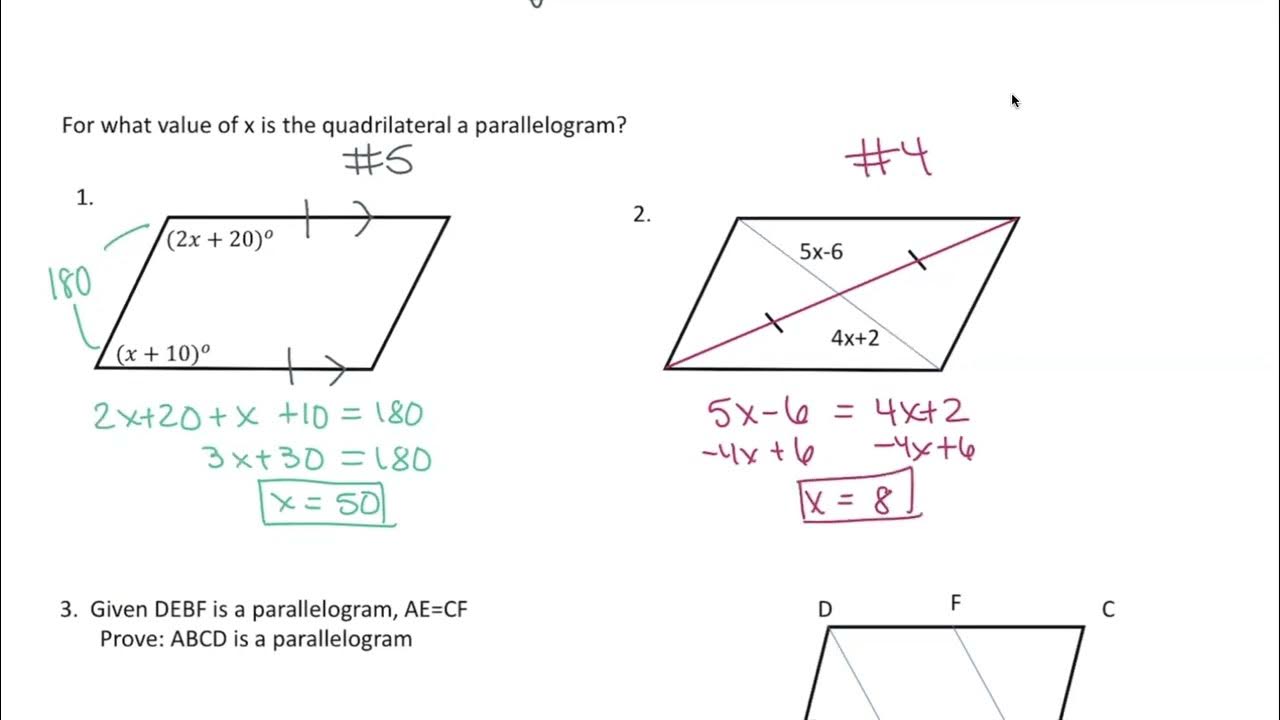
One of the defining features of a parallelogram is that opposite angles are congruent. This is a result of the parallel nature of its opposite sides which creates alternate interior angles between these sides. Here’s how you can use this property to prove a parallelogram:
- Identify the quadrilateral.
- Measure the angles or look for existing angle markings.
- Check if the opposite angles are equal.
Example:

In the image above, if ∠A = ∠C and ∠B = ∠D, then the shape is definitely a parallelogram.
💡 Note: This method is particularly useful when you can see angles or when measurements are provided.
The Midline Check

If you draw a diagonal in your quadrilateral and then connect the midpoints of the two non-adjacent sides, you’ll form what’s known as a midsegment. In a parallelogram, this midsegment is parallel to the sides it connects and is half its length. Here’s how you can leverage this property:
- Identify the midpoints of the non-adjacent sides.
- Connect these midpoints with a line segment.
- Verify that this line segment is parallel to the sides and is half its length.
Example:


As seen in the illustration, the midsegment MN is parallel to AB and half its length, proving the shape is a parallelogram.
⚠️ Note: When verifying the length of the midsegment, ensure you are halving the correct side length.
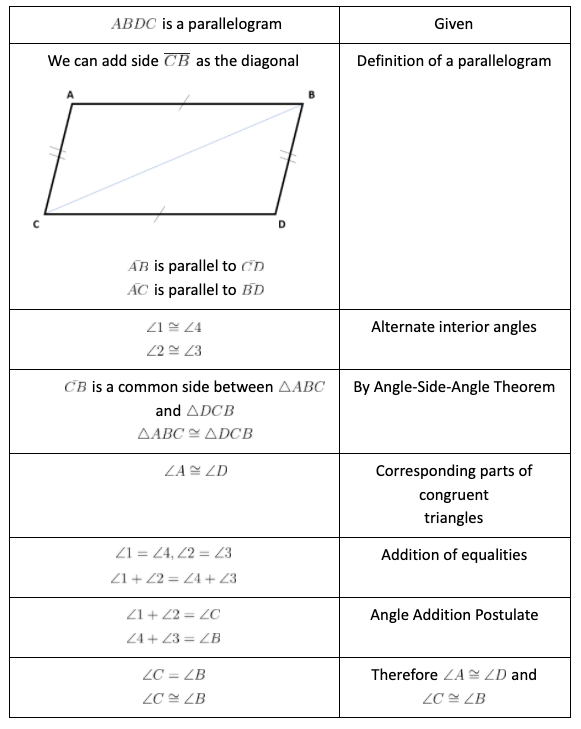
The Diagonal Bisectors Test
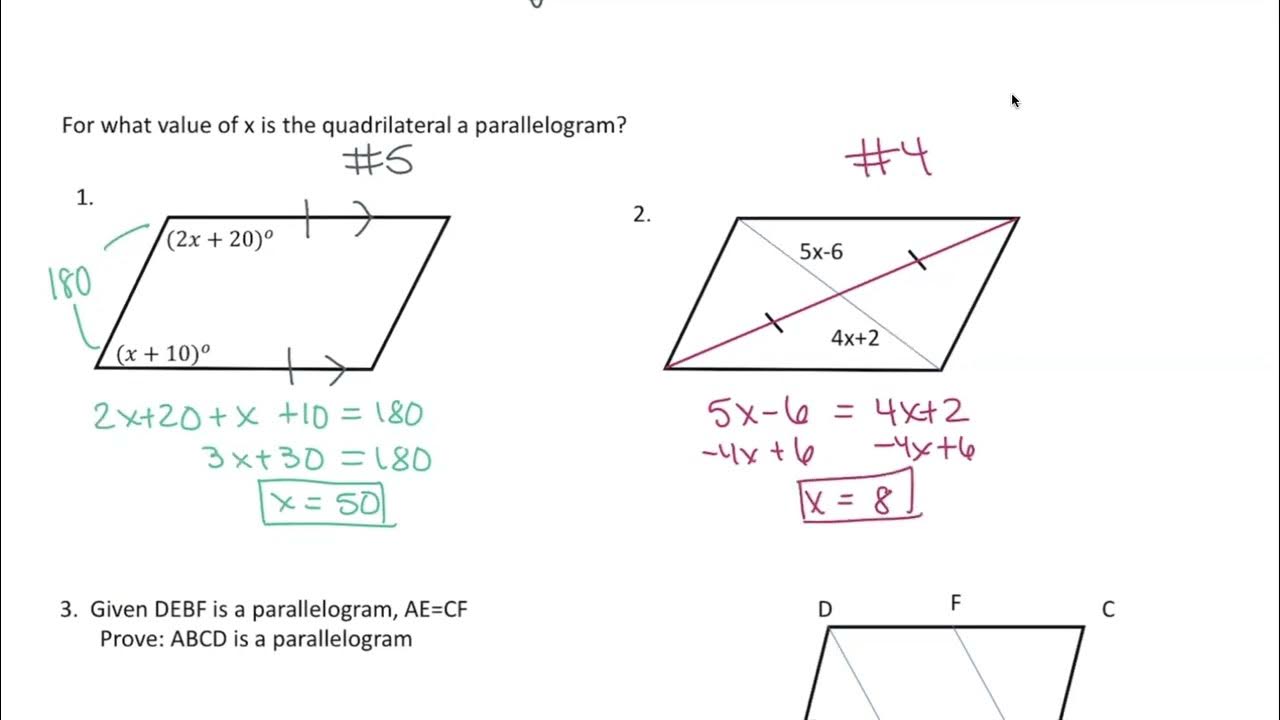
Parallelograms have diagonals that bisect each other, meaning they cut each other into two equal segments. This property offers another straightforward way to prove a parallelogram:
- Draw the diagonals of the quadrilateral.
- Identify the intersection point.
- Check if each diagonal splits the other into equal parts.
Example:

The image shows that when the diagonals cross, they split each other equally, confirming the quadrilateral as a parallelogram.
💡 Note: This method is particularly effective when you can draw diagonals without additional lines obstructing the measurement.
The Opposite Sides Check
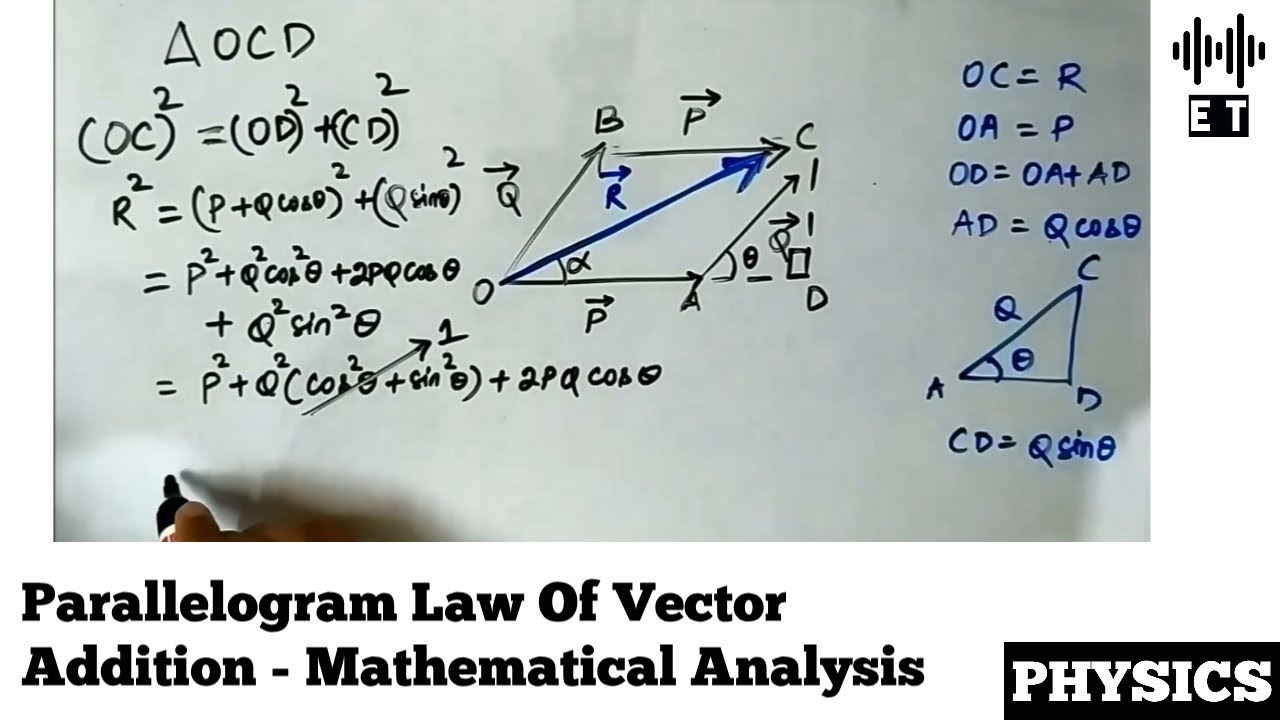
If you’ve noticed, opposite sides of a parallelogram are not only parallel but also congruent. This property is one of the most straightforward ways to prove a parallelogram:
- Identify the quadrilateral.
- Measure or observe the lengths of the sides.
- Check if opposite sides are equal.
Example:


In this diagram, if AB = CD and AD = BC, the shape is indeed a parallelogram.
🗝️ Note: This method is one of the easiest and most visually intuitive for proving a parallelogram.
The Cyclic Quadrilateral Property
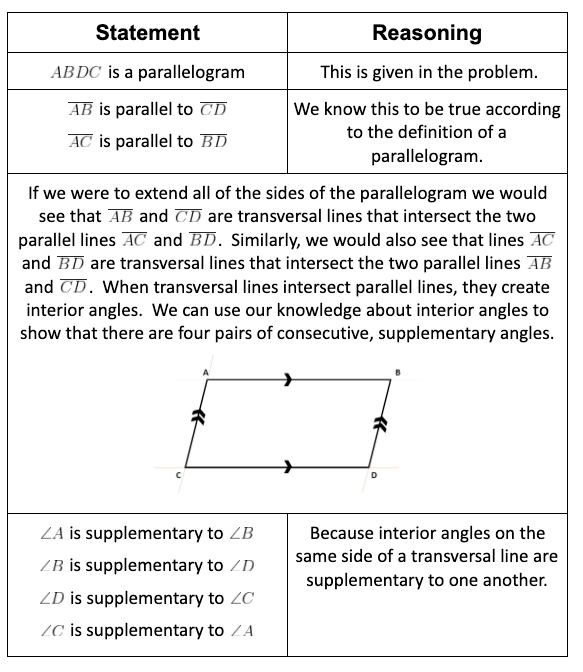
Lastly, if you can prove that a quadrilateral is cyclic (all vertices lie on a single circle), and its opposite angles sum to 180°, then it’s a parallelogram. This method can be less intuitive but powerful when applied correctly:
- Identify the quadrilateral.
- Check if it’s inscribed in a circle.
- Sum the opposite angles to see if they equal 180°.
Example:


The quadrilateral above, inscribed in a circle with opposite angles summing to 180°, is a parallelogram.
In this post, we’ve explored various methods to prove that a quadrilateral is a parallelogram, each offering unique insights into the properties of this geometric shape. Whether you’re using angles, side lengths, or even more advanced properties like cyclic quadrilaterals, you now have a toolkit to verify parallelograms with confidence. Each trick, from checking opposite angles to exploring the midline, provides a different perspective on the structural and spatial relationships that define a parallelogram.
As you explore geometry or encounter real-world parallelogram identification, remember these clever tricks can save you time and reduce frustration. They are not just mathematical tools but also conceptual aids that deepen your understanding of the geometric principles at play.
By mastering these methods, you’ll enhance not only your ability to prove geometric figures but also your appreciation for the elegance and logic of geometric reasoning.
What are the key characteristics of a parallelogram?

+
The key characteristics of a parallelogram include: - Opposite sides are parallel and equal in length. - Opposite angles are equal. - Consecutive angles sum to 180°. - Diagonals bisect each other. - It can be cyclic, with opposite angles summing to 180°.
How can I prove a parallelogram in real-life scenarios?
+
In real-life scenarios, you might: - Measure the lengths of opposite sides and see if they’re equal. - Check if opposite sides are parallel by observing their alignment. - Use construction tools or geometry software to verify that diagonals bisect each other.
What if my shape doesn’t meet these criteria?
+
If a quadrilateral doesn’t meet the criteria for a parallelogram, it might be another type of quadrilateral like a trapezoid, rectangle, square, or a kite, each with its unique properties and potential ways to prove them.