Prove Lines Parallel Worksheet: Geometry Made Easy

Understanding Parallel Lines in Geometry

Geometry is a fascinating branch of mathematics that deals with the study of shapes, sizes, and positions of objects. One of the fundamental concepts in geometry is parallel lines. In this blog post, we will delve into the world of parallel lines, explore their properties, and provide a comprehensive worksheet to help you practice and reinforce your understanding.
What are Parallel Lines?

Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, they are lines that are always the same distance apart and never touch. This concept is crucial in geometry, as it helps us understand the relationships between different shapes and objects.
Properties of Parallel Lines
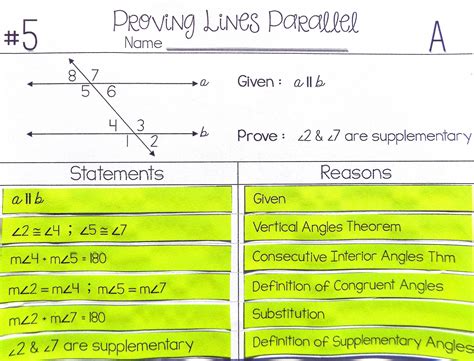
Parallel lines have several important properties that make them useful in geometry:
- Corresponding Angles: When two parallel lines are intersected by a transversal, the corresponding angles are equal. This means that if two angles are in the same relative position on the two lines, they are equal.
- Alternate Interior Angles: When two parallel lines are intersected by a transversal, the alternate interior angles are equal. This means that if two angles are on opposite sides of the transversal and inside the two lines, they are equal.
- Alternate Exterior Angles: When two parallel lines are intersected by a transversal, the alternate exterior angles are equal. This means that if two angles are on opposite sides of the transversal and outside the two lines, they are equal.
- Interior Angles on the Same Side of the Transversal: When two parallel lines are intersected by a transversal, the interior angles on the same side of the transversal are supplementary. This means that they add up to 180 degrees.
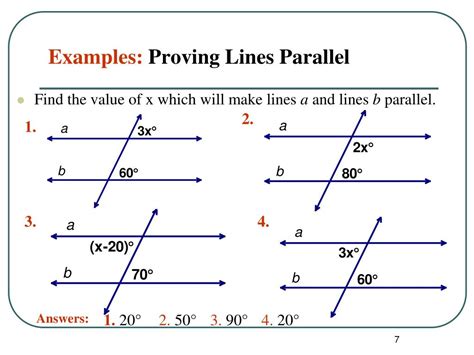
Proof Lines Parallel Worksheet
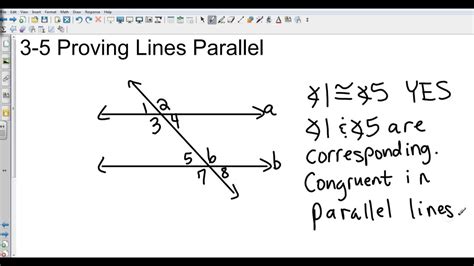
Now that we have explored the properties of parallel lines, it’s time to put your knowledge into practice. Here is a comprehensive worksheet to help you prove lines parallel:
Section 1: Multiple Choice Questions
Choose the correct answer for each question:
- If two lines are cut by a transversal and the corresponding angles are equal, what can be concluded about the lines? a) They are perpendicular b) They are parallel c) They are skew d) They are intersecting
Answer: b) They are parallel
- If two lines are cut by a transversal and the alternate interior angles are equal, what can be concluded about the lines? a) They are perpendicular b) They are parallel c) They are skew d) They are intersecting
Answer: b) They are parallel
- If two lines are cut by a transversal and the alternate exterior angles are equal, what can be concluded about the lines? a) They are perpendicular b) They are parallel c) They are skew d) They are intersecting
Answer: b) They are parallel
Section 2: Short Answer Questions
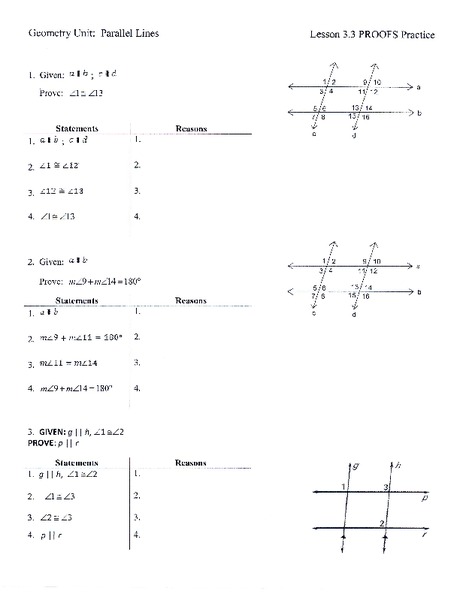
- Prove that if two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, then the lines are parallel.
Answer: Let’s assume that lines AB and CD are cut by a transversal EF. Let’s also assume that the interior angles on the same side of the transversal, ∠AFC and ∠BFD, are supplementary. This means that ∠AFC + ∠BFD = 180 degrees. Since ∠AFC and ∠BFD are supplementary, they must be equal. Therefore, ∠AFC = ∠BFD. By the definition of parallel lines, if two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel. Therefore, lines AB and CD are parallel.
Section 3: Proofs
- Prove that if two lines are parallel, then the corresponding angles are equal.
Answer: Let’s assume that lines AB and CD are parallel. Let’s also assume that EF is a transversal that intersects lines AB and CD. By the definition of parallel lines, lines AB and CD never intersect. Therefore, ∠AFC and ∠BFD are corresponding angles. Since lines AB and CD are parallel, ∠AFC and ∠BFD must be equal.
- Prove that if two lines are parallel, then the alternate interior angles are equal.
Answer: Let’s assume that lines AB and CD are parallel. Let’s also assume that EF is a transversal that intersects lines AB and CD. By the definition of parallel lines, lines AB and CD never intersect. Therefore, ∠AFC and ∠BFD are alternate interior angles. Since lines AB and CD are parallel, ∠AFC and ∠BFD must be equal.
📝 Note: Remember to always read the questions carefully and use the properties of parallel lines to help you solve the problems.
Conclusion

Parallel lines are a fundamental concept in geometry, and understanding their properties is crucial for solving problems and proving theorems. By practicing with this worksheet, you will become more confident in your ability to identify and work with parallel lines. Remember to always read the questions carefully and use the properties of parallel lines to help you solve the problems.
What is the definition of parallel lines?
+
Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended.
What are the properties of parallel lines?

+
Parallel lines have several important properties, including corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal.
How do I prove that two lines are parallel?
+
To prove that two lines are parallel, you need to show that the corresponding angles are equal, or that the alternate interior angles are equal, or that the alternate exterior angles are equal.
Related Terms:
- Prove lines parallel worksheet pdf
- proving lines parallel worksheet 3 3
- proving lines parallel proofs worksheet
- proving lines parallel instruction
- 3 3 proofs with parallel lines
- proofs with parallel lines worksheet