5 Proven Methods to Show Lines Are Parallel

In the realm of geometry, proving that two lines are parallel is fundamental for understanding spatial relationships and solving various geometric problems. This post will delve into five proven methods to demonstrate that lines are parallel, each based on different geometric principles and postulates. Whether you're a student tackling geometry assignments or an enthusiast revisiting mathematical foundations, these techniques will provide both the theoretical understanding and practical applications you need.
The Alternate Interior Angles Theorem
The Alternate Interior Angles Theorem is one of the most straightforward ways to prove lines are parallel. Here’s how it works:
- Identify a transversal line intersecting two lines.
- If the alternate interior angles (angles on opposite sides of the transversal, inside the two lines) are congruent, then the lines are parallel.
⚠️ Note: This theorem can be used in the converse form as well; if the lines are known to be parallel, then alternate interior angles will be equal.
The Corresponding Angles Postulate
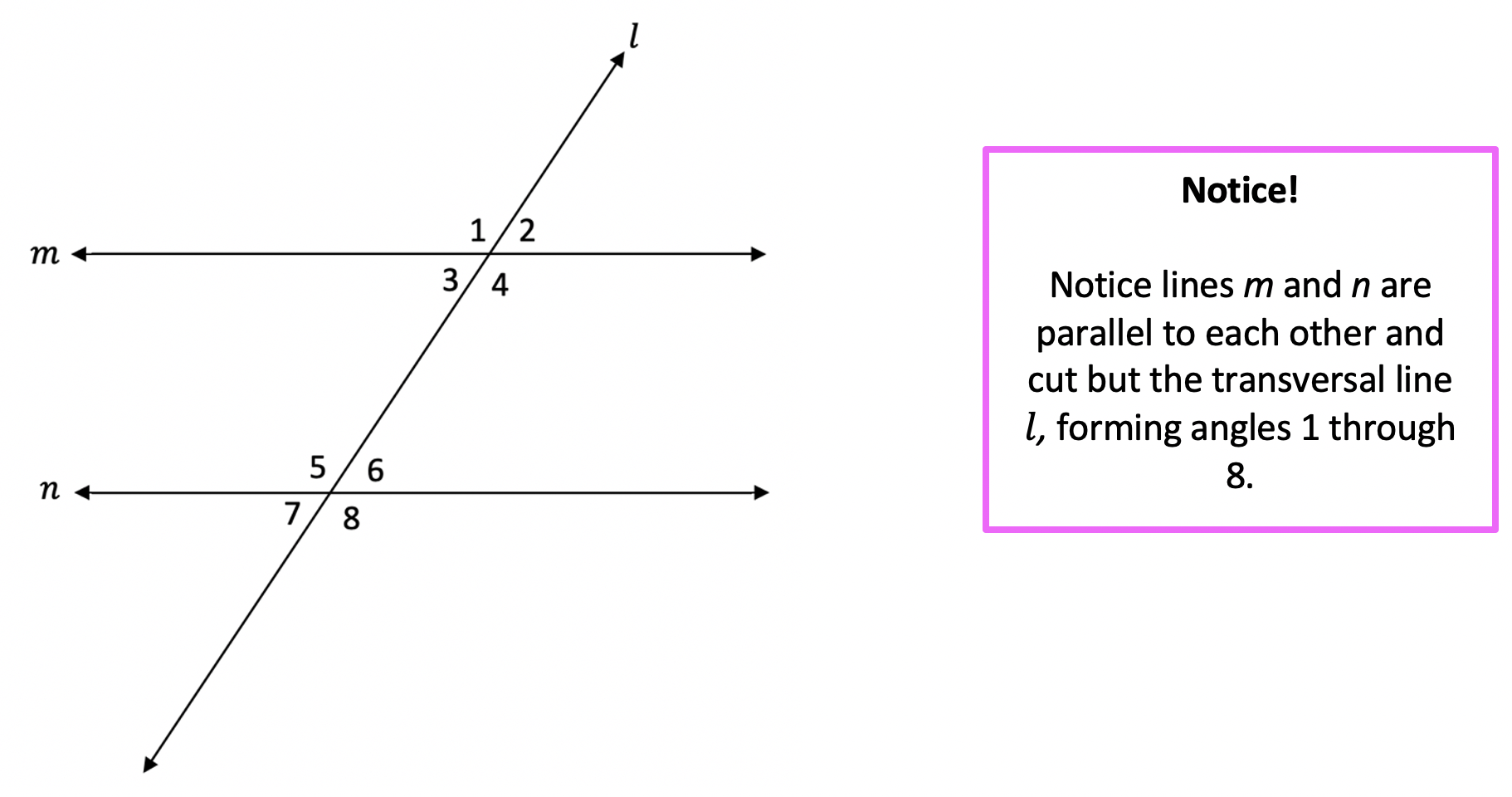
Corresponding angles are located on the same side of the transversal in corresponding positions relative to the two lines:
- If corresponding angles are congruent, the lines are parallel.
- This can also work in reverse; if lines are known to be parallel, then their corresponding angles will be equal.
Consecutive Interior Angles Theorem (Same-Side Interior Angles)
The sum of consecutive interior angles, also known as same-side interior angles, gives us:
- If these angles are supplementary, which means they add up to 180 degrees, then the lines are parallel.
- This theorem is often used in conjunction with the Parallel Line Postulate to prove lines parallel.
| Angle Relationship | Consequence |
|---|---|
| Alternate Interior Angles are Congruent | Lines are Parallel |
| Corresponding Angles are Congruent | Lines are Parallel |
| Consecutive Interior Angles are Supplementary | Lines are Parallel |

The Perpendicular Transversal Theorem

This theorem posits:
- If two lines are perpendicular to the same line (the transversal), they must be parallel to each other.
📐 Note: Perpendicularity here means a 90-degree angle, making this a straightforward method to understand and apply.
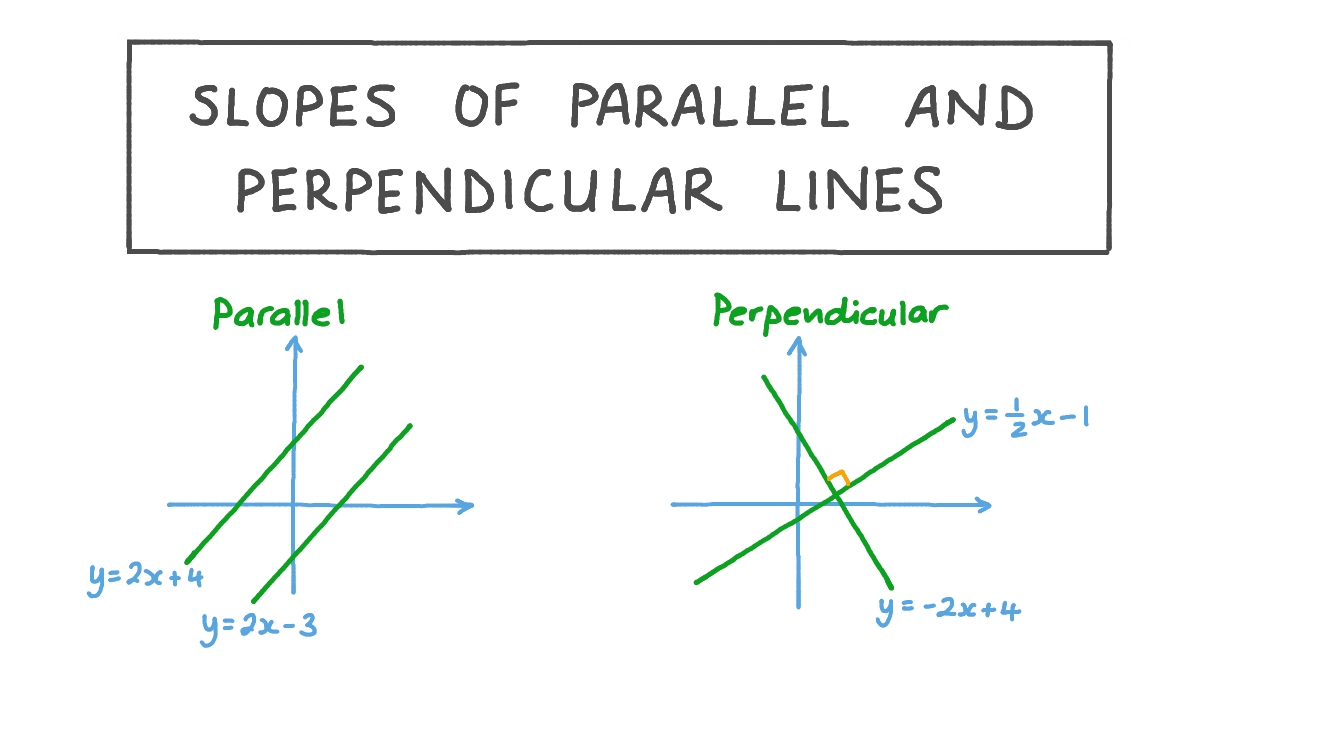
Slope and Coordinate Geometry
While not strictly a theorem of traditional geometry, this method is crucial in coordinate geometry:
- If two lines have the same slope, they are parallel. In coordinate geometry, this can be easily verified by calculating the slopes of two lines from their equations.
- Equation for slope: m = (y2-y1) / (x2-x1)
This approach introduces the use of algebra in geometry, which can be particularly helpful when working with non-Euclidean geometry or complex coordinate problems.
In summary, the beauty of parallel lines in geometry lies in the multitude of ways they can be proven parallel. From theorems that hinge on angle relationships to algebraic approaches using slopes, each method offers a different perspective on how lines interact in space. By mastering these techniques, you not only enhance your geometric intuition but also equip yourself with versatile tools for solving a wide array of geometric challenges. Whether you're constructing proofs, designing structures, or exploring spatial relationships, understanding these methods will serve as a fundamental skill in your mathematical toolkit.
What if the lines are not straight?
+
These methods apply specifically to straight lines. For curved or non-straight lines, parallel concepts require more complex geometry such as differential geometry or the study of geodesics in curved spaces.
Can these methods be used with 3D geometry?

+
Yes, but in three dimensions, you often need to consider planes rather than just lines. The principles of parallel lines extend into this realm, but the application requires understanding the plane on which the lines lie.
How do I prove two lines are not parallel?

+
To show lines are not parallel, you can disprove the conditions of these theorems. For example, if corresponding angles or alternate interior angles are not congruent, or if slopes differ in coordinate geometry, the lines are not parallel.



