7th Grade Proportional Relationships Worksheet Guide

In 7th grade, students are introduced to proportional relationships, which is a pivotal topic for understanding how quantities can be related to each other in a consistent manner. Proportional relationships not only prepare students for algebra but also provide a foundation for understanding everyday phenomena such as scaling recipes, calculating taxes, and interpreting data from charts and graphs. This guide will explore how to effectively teach and understand proportional relationships through worksheet activities, offering practical tips and insights.
Understanding Proportional Relationships

A proportional relationship is when two quantities grow or shrink at the same rate, maintaining a constant ratio. Here’s how you can explain it to students:
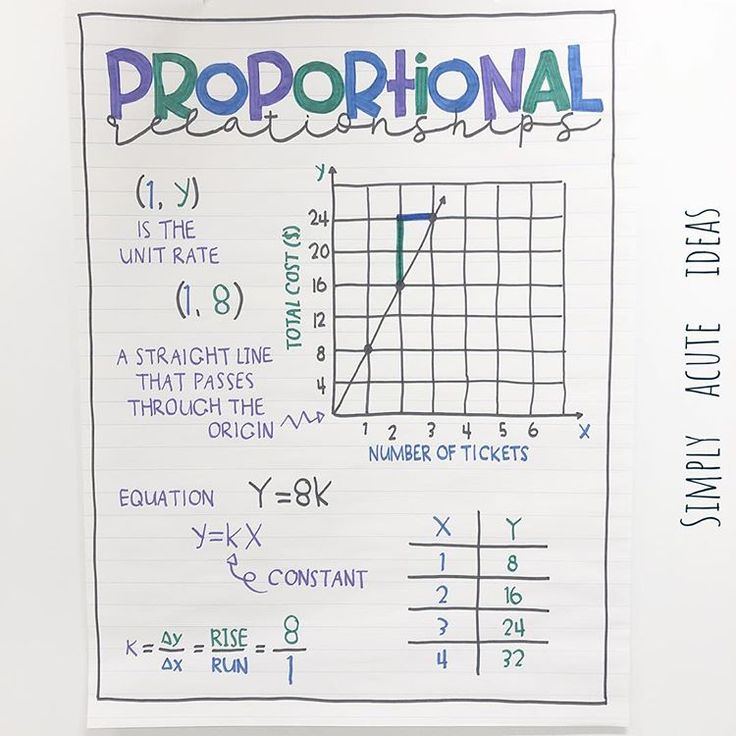
- Definition: If one quantity is always the product of the other quantity and some constant (k), then the relationship is proportional. Algebraically, this can be expressed as y = kx where k is the constant of proportionality.
- Example: If you travel at a constant speed of 60 miles per hour, the distance you travel (y) is proportional to the time (x) with k = 60, so y = 60x.
💡 Note: Ensure students understand that in a proportional relationship, the graph will always pass through the origin (0, 0).
Worksheet Design and Usage

Worksheets are an essential tool for reinforcing concepts. Here’s how to design and use them effectively for teaching proportional relationships:
Step-by-Step Guide:

- Identification of Proportionality: Include exercises where students identify if a given set of data or graph represents a proportional relationship. Provide tables where students calculate the constant of proportionality.
Time (hours) Distance (miles) Constant (k) 1 60 60 2 120 60 3 180 60 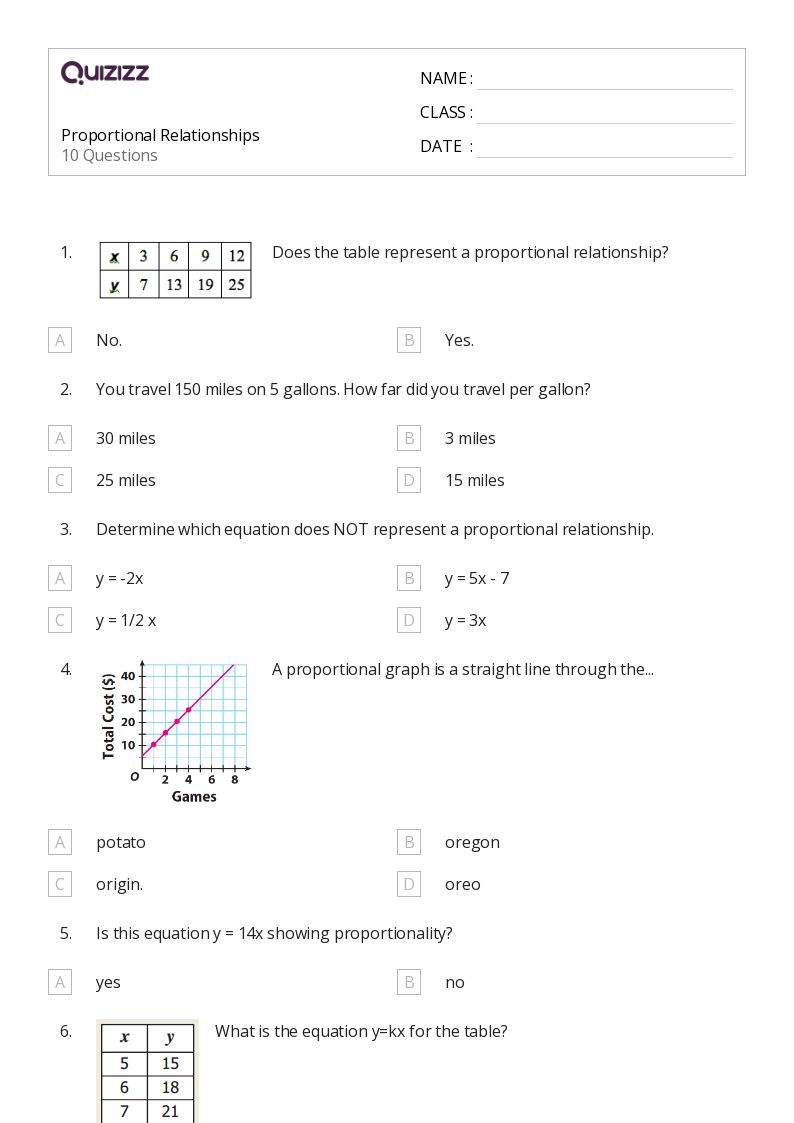
- Graphing: Ask students to plot points on graph paper. This visual representation helps in recognizing patterns.

- Word Problems: Use real-life scenarios where students must determine if situations exhibit proportionality. For example, pricing items in bulk, recipe conversions, or travel distances based on time.
- Practice with Equations: Provide problems where students solve for x or y in proportional relationships, like 3y = 2x.
- Constant of Proportionality: Include problems where students calculate the constant k when given two related quantities.
💡 Note: Allow students to discuss their findings and justify why a relationship is proportional or not, fostering critical thinking.
Practical Examples

Here are some practical exercises to incorporate into your worksheets:
- Convert a recipe that serves 4 to serve 12 by finding the proportionality factor.
- Determine if a car’s fuel efficiency (miles per gallon) is constant over different amounts of fuel used.
- Scale up or down the dimensions of a model to see how surface area and volume change proportionally.
Engaging Students with Technology

Using technology can make learning more interactive:
- Interactive Graphs: Use tools like Desmos or GeoGebra where students can manipulate graphs to see changes in proportionality.
- Apps and Websites: Utilize educational platforms like Khan Academy, which offer exercises specifically tailored for proportional relationships.
- Digital Worksheets: Provide digital versions of worksheets where students can input data and immediately see if their answers show proportionality.
💡 Note: Technology not only makes learning fun but also immediate feedback helps students learn from their mistakes quickly.
In summary, teaching proportional relationships in 7th grade through structured worksheet activities equips students with a crucial mathematical tool for understanding and applying math in various contexts. By focusing on identification, graphing, problem-solving, and practical application, educators can ensure that students grasp the essence of proportionality, preparing them for future mathematical challenges. This approach fosters a deep understanding of how quantities relate and interact in the real world, enhancing their analytical and logical reasoning skills.
How do I know if a graph represents a proportional relationship?

+
A graph represents a proportional relationship if it is a straight line that passes through the origin (0,0). This means for every x-value, the corresponding y-value is directly proportional to it.
What is the significance of the constant k in proportional relationships?

+
The constant k, or the constant of proportionality, indicates the rate at which y increases for every unit increase in x. It shows the fixed ratio between the two quantities.
Can proportional relationships have a negative constant of proportionality?
+
Yes, proportional relationships can have a negative k. This means that as one quantity increases, the other decreases by a consistent factor.