Rhombus Properties: Interactive Worksheet Guide
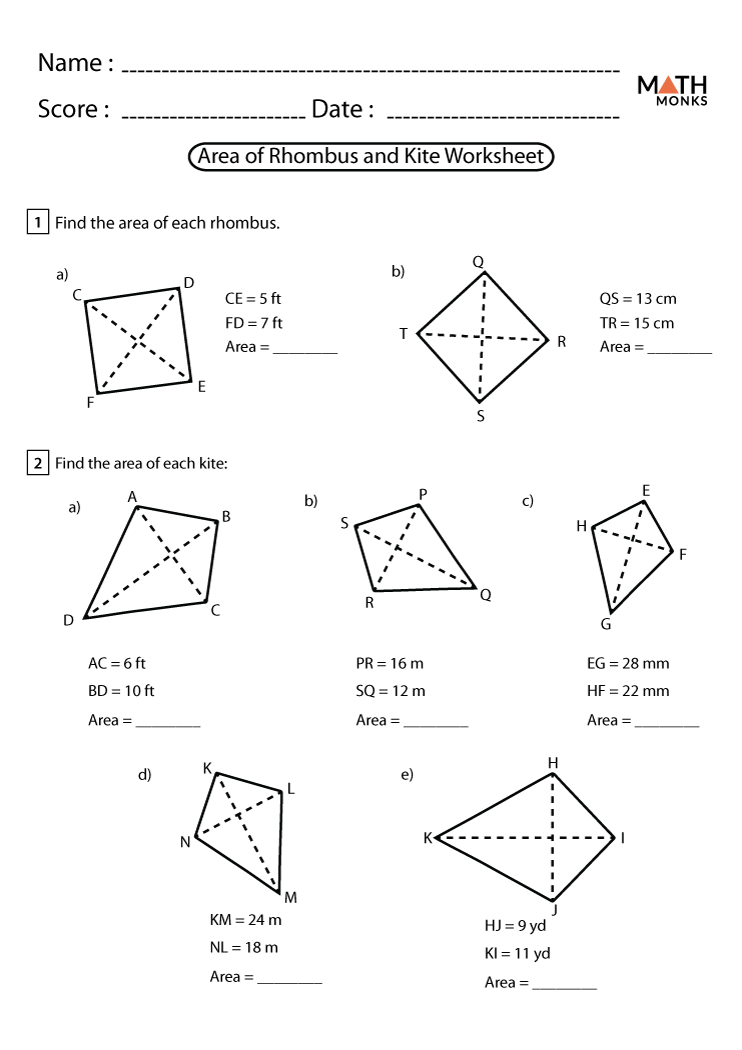
If you've ever wondered how the unique attributes of a rhombus can help you solve geometric problems or if you're simply looking to sharpen your skills in geometric shapes, then this interactive worksheet guide is your go-to resource. Rhombuses, with their distinctive properties, are fascinating shapes that hold both educational and practical value. Let's dive in and explore the properties, formulas, and potential applications of rhombuses with our interactive worksheet guide.
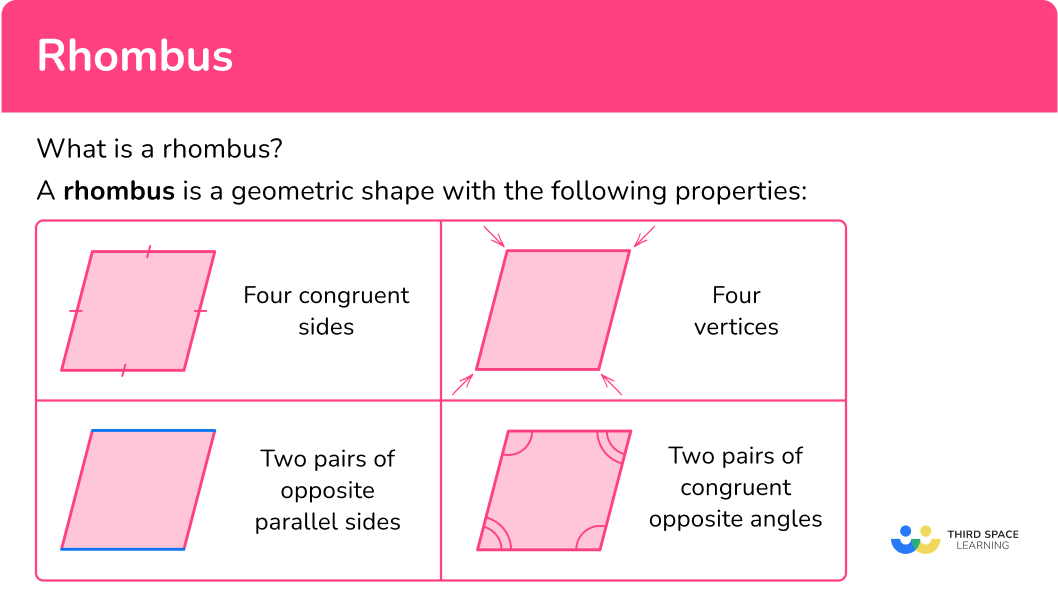
What is a Rhombus?

A rhombus is a type of quadrilateral with four sides of equal length. It’s often confused with a square due to its uniformity, but unlike squares, the diagonals of a rhombus do not necessarily meet at right angles, making them a unique shape in geometry. Here are some core properties of a rhombus:
- All sides are of equal length.
- Opposite angles are equal.
- Diagonals bisect each other at right angles.
- Each diagonal bisects two angles of the rhombus.
- The sum of the interior angles is 360°.

Interacting with Rhombus Properties
The interactive worksheet we’re discussing is designed to help you understand and practice rhombus properties through several engaging activities:
- Property Identification: You'll be presented with different rhombuses and asked to identify which properties they exhibit.
- Measurement Exploration: You'll calculate the lengths of sides and diagonals, as well as determine the measure of angles.
- Visual Recognition: Spotting rhombuses within more complex shapes or patterns, enhancing your visual-spatial intelligence.
- Constructing Rhombuses: Using given parameters like side length or diagonal length, construct a rhombus to visualize its properties firsthand.
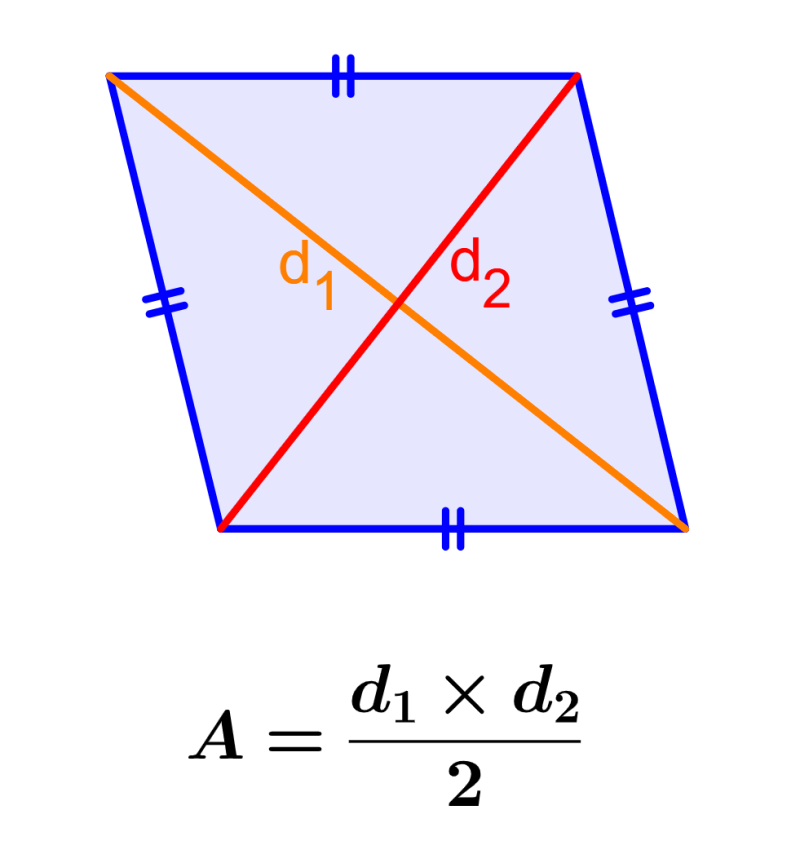
Exploring Rhombus Formulas
Now that we’ve established the properties, let’s look into the mathematical formulas that are essential for working with rhombuses:
| Property | Formula |
|---|---|
| Side Length | s |
| Perimeter | 4s |
| Area using Diagonals | 0.5 * d1 * d2 |
| Area using Side and Trigonometric Function | s2 * sin(α) |

🔍 Note: Here, d1 and d2 are the lengths of the diagonals, and α is one of the angles of the rhombus.
Real-World Applications
Understanding rhombuses isn’t just theoretical; their properties are utilized in several real-world scenarios:
- Architecture and Design: Rhombuses appear in flooring patterns, wall tiles, and even in the design of some buildings to create visually appealing and mathematically balanced layouts.
- Engineering: Trusses and frameworks often use rhombic patterns because of their strength and the ability to withstand forces effectively.
- Jewelry and Fashion: Diamond cuts often take the shape of a rhombus, leveraging their symmetry to enhance visual appeal.
Using the Interactive Worksheet

Here’s how to make the most out of this interactive rhombus worksheet:
- Start with Basics: Begin by reviewing basic rhombus properties.
- Practice: Engage with problems that require you to calculate or verify properties of given rhombuses.
- Challenge Yourself: As you become more comfortable, tackle advanced problems that might combine multiple properties or require more complex geometric reasoning.
- Utilize Visuals: Use the worksheet's interactive elements to drag, adjust, and explore rhombus properties visually.
📚 Note: Remember, consistency is key. Regular practice with this worksheet will solidify your understanding of rhombuses and improve your geometric intuition.
As we wrap up this guide, it’s clear that mastering the properties of a rhombus goes beyond just memorizing facts; it’s about applying those properties in diverse contexts, from mathematical problem-solving to real-world applications. The interactive nature of this worksheet ensures that your learning experience is not only informative but also engaging, allowing for a deeper understanding of this fascinating shape.
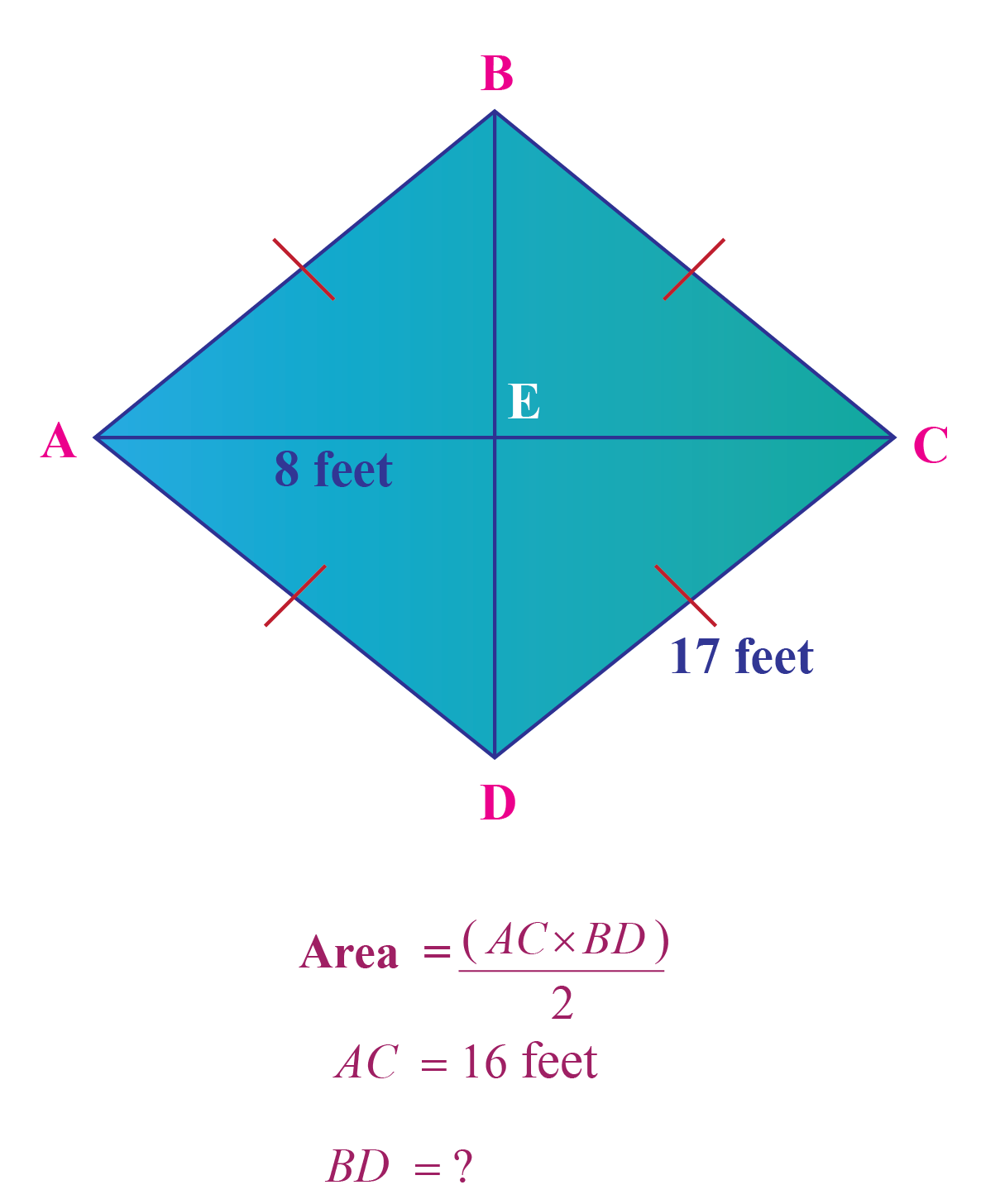
Why are the diagonals of a rhombus important?

+
The diagonals of a rhombus bisect each other at right angles, forming four right triangles. This property is crucial for finding the area, proving properties, and solving geometric problems involving rhombuses.
Can a rhombus be a square?

+
A square can be considered a special type of rhombus where all angles are 90°, but not all rhombuses are squares.
How does this interactive worksheet help in learning?
+
By providing immediate feedback, visual aids, and practical examples, the interactive worksheet enhances understanding through hands-on experience, making learning more interactive and less abstract.