5 Essential Properties of Parallelograms Worksheet Answers

Welcome to your detailed guide on the essential properties of parallelograms. Understanding these properties not only helps in solving mathematical problems but also in real-world applications where structures and shapes play a pivotal role. Let's dive into the fascinating world of parallelograms and explore why they're so significant in geometry.
What are Parallelograms?

A parallelogram is a quadrilateral with two pairs of parallel sides. This simple definition opens up to a myriad of interesting properties and characteristics:
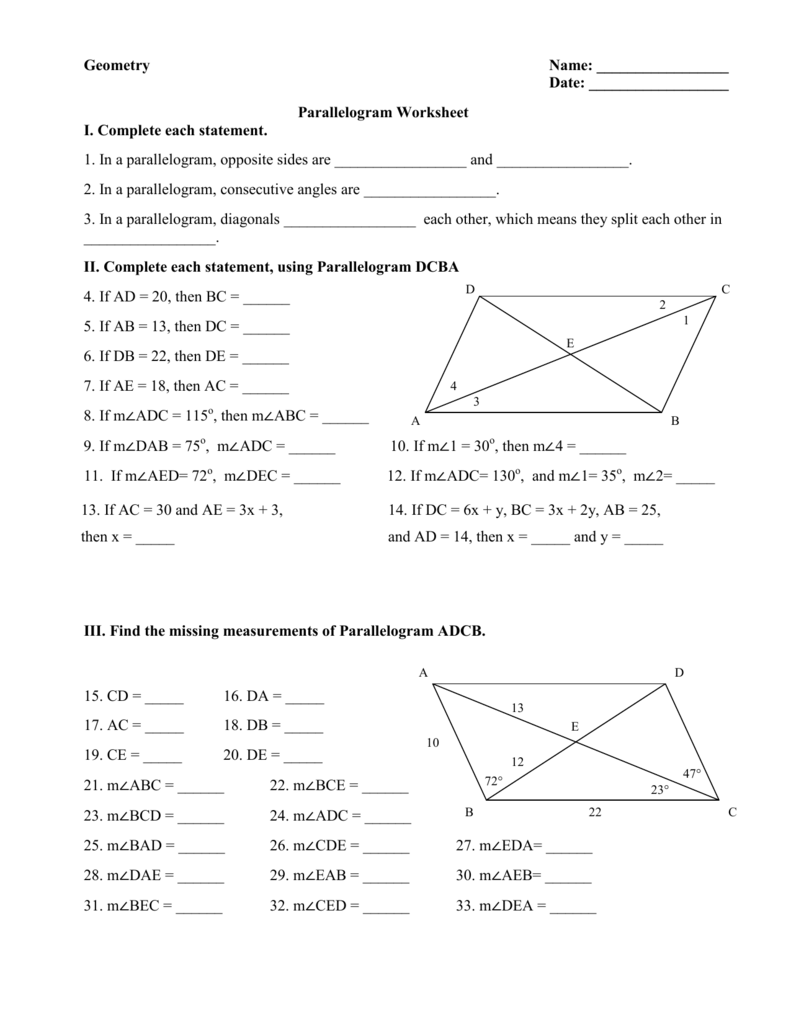
- Opposite sides are equal in length: If one side is 5 cm, the opposite side must also be 5 cm.
- Opposite angles are equal: Angles opposite to each other in a parallelogram are congruent.
- Consecutive angles are supplementary: The sum of two adjacent angles is 180 degrees.
- Diagonals bisect each other: The intersection point of the diagonals divides each into two equal segments.
- Symmetry: A parallelogram might have one or two lines of symmetry depending on its type.
Exploring the Properties

Here’s a closer look at each property to understand how they play out in different scenarios:
1. Opposite Sides Equal

When you draw a parallelogram, you’ll notice that the opposite sides are parallel to each other, which naturally leads to them being equal in length. This property simplifies calculations in geometry, as knowing the length of one side can help you determine the dimensions of the entire shape.
2. Opposite Angles Equal

This property is a direct result of the parallel sides. If you know one angle, you automatically know its opposite angle, which aids in designing and analyzing structures where angles are crucial.
3. Consecutive Angles Supplementary

In any parallelogram, if you add the measures of any two consecutive angles, the sum will always be 180 degrees. This ensures stability and balance in the shape, making it useful in various architectural designs.
4. Diagonals Bisecting Each Other

The diagonals of a parallelogram intersect at their midpoints. This can be visualized as if the parallelogram has two pairs of intersecting lines, each dividing the other into equal parts. This property has practical applications in engineering, particularly in ensuring structural integrity.
🔎 Note: If one diagonal is 10 cm, each half-diagonal (from the intersection to an endpoint) will be 5 cm.
5. Symmetry

Parallelograms can exhibit either rotational symmetry or both rotational and reflective symmetry. Here’s how they manifest:
- Rotational Symmetry: A rhombus (a special type of parallelogram where all sides are equal) can rotate 180 degrees around its center and look the same.
- Reflective Symmetry: A rectangle has one line of symmetry through the center, and a square has two.
| Property | Definition | Example |
|---|---|---|
| Opposite Sides Equal | AB = CD, AD = BC in any parallelogram | If AD = 6 cm, then BC must also be 6 cm |
| Opposite Angles Equal | ∠A = ∠C, ∠B = ∠D | If ∠A is 60°, ∠C must also be 60° |
| Consecutive Angles Supplementary | ∠A + ∠B = 180°, ∠B + ∠C = 180° | If ∠A is 100°, ∠B must be 80° |
| Diagonals Bisect Each Other | AC and BD intersect at point E; AE = EC, BE = ED | If AC is 8 cm, AE = EC = 4 cm |
| Symmetry | Varies with type of parallelogram | A rectangle has one line of symmetry |
In conclusion, the properties of parallelograms are not just academic curiosities but have real-world applications in fields like architecture, engineering, and design. By understanding these properties, one can analyze structures, ensure stability in constructions, and even solve complex mathematical problems with relative ease. The symmetrical nature and balanced dimensions of parallelograms provide both aesthetic appeal and functional efficiency, making them a staple in geometric and practical applications.
Why do opposite sides of a parallelogram have to be equal?

+
Because in a parallelogram, opposite sides are parallel, and parallel lines on a plane have the same direction, leading to the sides being of equal length.
Can the diagonals of a parallelogram be unequal?

+
Yes, in a general parallelogram, diagonals are not necessarily equal, although they bisect each other.
How does understanding parallelogram properties help in architecture?

+
Understanding these properties allows architects to design buildings and structures that are stable, visually appealing, and functional, utilizing the strengths and symmetries of geometric shapes.
Can you find the area of a parallelogram knowing only its diagonals?

+
Yes, the area of a parallelogram can be calculated by multiplying the lengths of its diagonals and then dividing by 2, as long as you know the sine of the angle between them.


