5 Essential Properties of Exponents

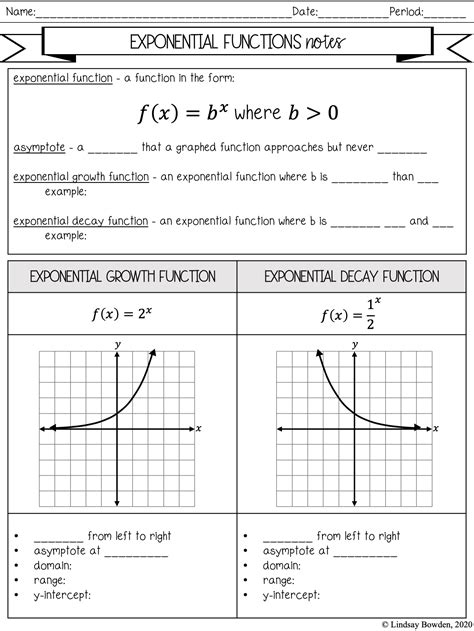
Understanding Exponents and Their Properties

Exponents are a fundamental concept in mathematics, and understanding their properties is crucial for solving various mathematical problems. Exponents are used to represent repeated multiplication of a number by itself. In this article, we will explore five essential properties of exponents that will help you to better understand and work with exponents.
Property 1: Product of Powers

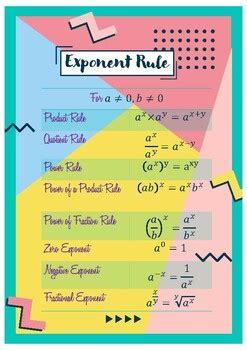
The product of powers property states that when we multiply two numbers with the same base, we can add the exponents. This property is represented as:
a^m × a^n = a^(m+n)
For example:
2^3 × 2^4 = 2^(3+4) = 2^7
This property helps us to simplify expressions by combining the exponents.
Property 2: Power of a Power

The power of a power property states that when we raise a number to a power, and then raise that result to another power, we can multiply the exponents. This property is represented as:
(a^m)^n = a^(m×n)
For example:
(2^3)^4 = 2^(3×4) = 2^12
This property helps us to simplify expressions by multiplying the exponents.
Property 3: Zero Exponent

The zero exponent property states that any number raised to the power of zero is equal to 1. This property is represented as:
a^0 = 1
For example:
2^0 = 1
This property helps us to simplify expressions by eliminating the exponent.
Property 4: Negative Exponent
The negative exponent property states that a number raised to a negative power is equal to the reciprocal of the number raised to the positive power. This property is represented as:
a^(-n) = 1/a^n
For example:
2^(-3) = 1⁄2^3 = 1⁄8
This property helps us to simplify expressions by converting negative exponents to positive exponents.
Property 5: Quotient of Powers

The quotient of powers property states that when we divide two numbers with the same base, we can subtract the exponents. This property is represented as:
a^m ÷ a^n = a^(m-n)
For example:
2^5 ÷ 2^3 = 2^(5-3) = 2^2
This property helps us to simplify expressions by subtracting the exponents.
📝 Note: These properties can be combined to simplify complex expressions involving exponents.
| Property | Description | Example |
|---|---|---|
| Product of Powers | a^m × a^n = a^(m+n) | 2^3 × 2^4 = 2^7 |
| Power of a Power | (a^m)^n = a^(m×n) | (2^3)^4 = 2^12 |
| Zero Exponent | a^0 = 1 | 2^0 = 1 |
| Negative Exponent | a^(-n) = 1/a^n | 2^(-3) = 1/2^3 |
| Quotient of Powers | a^m ÷ a^n = a^(m-n) | 2^5 ÷ 2^3 = 2^2 |

By understanding and applying these five essential properties of exponents, you can simplify complex expressions and solve mathematical problems with ease.
In summary, exponents are a fundamental concept in mathematics, and understanding their properties is crucial for solving various mathematical problems. The five essential properties of exponents are the product of powers, power of a power, zero exponent, negative exponent, and quotient of powers. By applying these properties, you can simplify complex expressions and solve mathematical problems with ease.
What is an exponent?

+
An exponent is a number that represents the power to which a base number is raised.
What is the product of powers property?

+
The product of powers property states that when we multiply two numbers with the same base, we can add the exponents.
What is the power of a power property?
+
The power of a power property states that when we raise a number to a power, and then raise that result to another power, we can multiply the exponents.
Related Terms:
- Properties of Exponents Worksheet PDF
- simplify properties of exponents practice
- properties of exponents practice pdf
- free printable exponent worksheets
- properties of exponential functions worksheet
- properties of exponents kuta pdf