5 Essential Properties of Quadrilaterals Explained
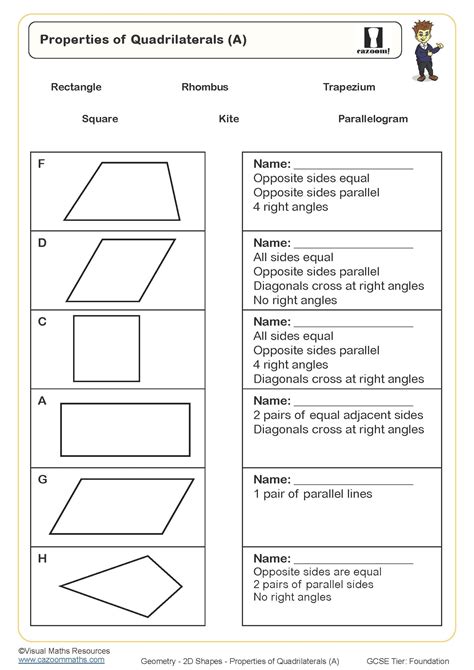
In the vast expanse of geometric shapes, quadrilaterals stand out for their commonality and practical applications in real-world scenarios like architecture, design, and engineering. As a fundamental component of geometry, understanding the essential properties of quadrilaterals not only enriches one's grasp of mathematical concepts but also aids in problem-solving across various disciplines. This blog post dives into five key properties of quadrilaterals, offering insights into their unique characteristics.
1. Sum of Interior Angles

One of the most fundamental properties of any quadrilateral is the sum of its interior angles:
- The sum of the interior angles in a quadrilateral always equals 360 degrees.
- This property arises because a quadrilateral can be divided into two triangles, each with an internal angle sum of 180 degrees.
This rule holds true for all types of quadrilaterals, whether they are rectangles, squares, rhombuses, trapezoids, or irregular shapes.
📌 Note: This property applies even if the quadrilateral is irregular or not planar, although in non-planar cases, the sum might vary due to the angles not lying on a single plane.
2. Opposite Angles in Parallelograms

When discussing parallelograms, which are a subset of quadrilaterals with opposite sides parallel:
- The opposite angles in a parallelogram are equal.
- Additionally, consecutive angles (angles next to each other) sum up to 180 degrees, making them supplementary.
| Property | Description |
|---|---|
| Opposite Angles | Equal in measure |
| Consecutive Angles | Sum to 180° |

3. Diagonals in Rectangles and Squares

In rectangles and squares, diagonals come with special properties:
- The diagonals bisect each other, meaning they split each other into two equal parts.
- In squares, diagonals are also perpendicular to each other.
This intersection property helps in construction and design, allowing for symmetry and structural integrity.
4. Cyclic Quadrilaterals

Cyclic quadrilaterals, which are quadrilaterals whose vertices all lie on a single circle, have a fascinating property:
- The opposite angles sum to 180 degrees. This characteristic is often used in geometric problems involving inscribed polygons.
5. Symmetry in Isosceles Trapezoids

Among special quadrilaterals, the isosceles trapezoid stands out:
- The diagonals are equal in length.
- The trapezoid has a line of symmetry, which passes through the midpoints of the two non-parallel sides, dividing the trapezoid into two congruent triangles.
💡 Note: When discussing symmetry, the term "isosceles" signifies that the trapezoid has legs of equal length, much like an isosceles triangle.
In wrapping up our exploration of quadrilateral properties, we find that these shapes are not only mathematically intriguing but also immensely practical. From the architectural design of buildings to the precision needed in mechanical engineering, understanding the properties of quadrilaterals helps us tackle complex problems with mathematical elegance and accuracy. Whether it's ensuring structural stability in a bridge or calculating surface areas for art and decoration, the foundational knowledge of quadrilaterals enriches both theoretical and practical aspects of geometry.
What makes a quadrilateral different from other polygons?

+
A quadrilateral is a polygon with exactly four sides. This basic classification sets it apart from triangles, pentagons, hexagons, and other polygons with a different number of sides.
Can all quadrilaterals be considered as parallelograms?

+
No, not all quadrilaterals are parallelograms. Parallelograms are a subset of quadrilaterals where opposite sides are parallel. Trapezoids, for example, have only one pair of parallel sides and thus are not parallelograms.
What is the importance of the cyclic property in quadrilaterals?

+
The cyclic property of quadrilaterals is crucial in geometric proofs and problems. It provides a tool for solving angle relationships and inscribing shapes in circles, simplifying complex geometric calculations.
How can the properties of quadrilaterals be applied in real life?

+
Properties of quadrilaterals are used in architecture for design symmetry, in mechanical engineering for component stability, in graphics for art and design, and even in fashion to create symmetrical clothing patterns.



