5 Key Properties of Parallelograms You Need to Know

When delving into the world of geometry, understanding the properties of various shapes is crucial for both mathematical proficiency and applications in the real world. Parallelograms, with their unique characteristics, stand out for their utility in numerous fields including architecture, engineering, and design. Here, we will explore the five key properties of parallelograms that you should know to enhance your understanding and appreciation of these fascinating geometric figures.
1. Opposite Sides are Parallel and Equal in Length
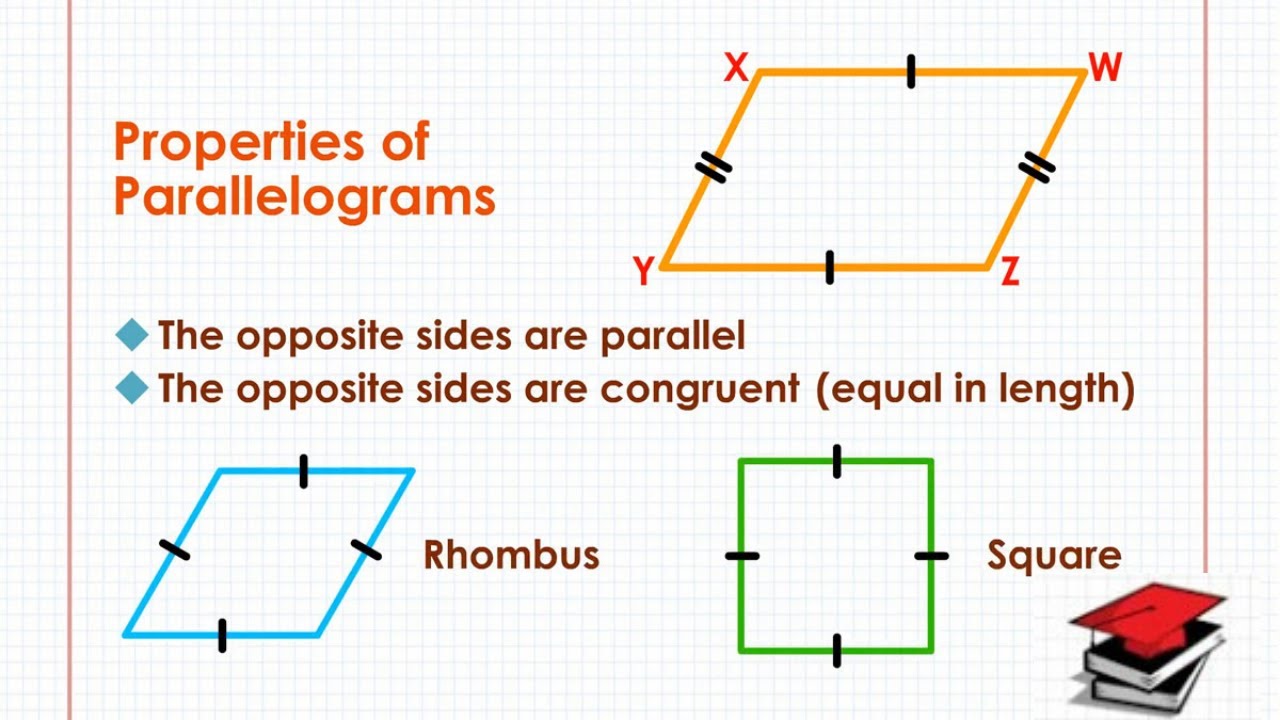

One of the defining characteristics of a parallelogram is that the opposite sides are both parallel to each other and equal in length. This property allows us to identify a parallelogram easily. If you measure the distance between any two parallel sides, they will always be the same.
- AB = CD (both in length and parallel)
- AD = BC (both in length and parallel)
2. Opposite Angles are Equal


In a parallelogram, the opposite angles are not just similar in shape; they are equal. This symmetry offers a delightful visual balance to the shape:
- Angle A = Angle C
- Angle B = Angle D
This property also provides a way to solve for missing angles when only one angle is known.
3. Consecutive Angles are Supplementary

Each pair of adjacent or consecutive angles in a parallelogram sum up to 180 degrees. This property stems from the fact that these angles are located on a straight line, also known as a linear pair.
- Angle A + Angle B = 180°
- Angle B + Angle C = 180°
- Angle C + Angle D = 180°
- Angle D + Angle A = 180°
4. Diagonals Bisect Each Other


The diagonals in a parallelogram have a special relationship; they bisect one another, meaning that each diagonal divides the other into two equal segments. This property is often used to prove that a quadrilateral is indeed a parallelogram:
- Diagonal AC bisects diagonal BD, and vice versa
- The point of intersection (O) divides the diagonals in half
5. Area and Perimeter Formulas

| Property | Formula |
|---|---|
| Area | A = base × height |
| Perimeter | P = 2 × (side1 + side2) |

These formulas are straightforward but are rooted in the properties mentioned above, particularly the equal length of opposite sides and the ability to find height by dropping perpendicular lines from one side to another.
These properties of parallelograms are not just mathematical curiosities; they have practical implications:
- Understanding structural integrity in architecture, where balanced forces are crucial.
- In mechanical engineering, to ensure symmetrical distribution of forces.
- For designing patterns in textiles or art, where symmetry and balance are sought after.
💡 Note: Keep in mind that not all quadrilaterals are parallelograms. For a quadrilateral to be considered a parallelogram, it must meet all of these key properties, not just one or two.
As we've journeyed through the properties of parallelograms, we've seen how they provide a balanced and beautiful structure in both the abstract world of mathematics and the concrete world around us. They embody symmetry, equality, and the principles of balance, making them an essential part of geometry. The symmetry and balance of parallelograms can teach us about harmony in our own lives, reminding us that there are always ways to bring order and structure to what might seem chaotic.
What is the difference between a parallelogram and a rectangle?

+
While both shapes have opposite sides that are equal and parallel, a rectangle has an additional property where all angles are right angles (90°). A parallelogram can have any angle sum to 180° for adjacent angles, but they are not necessarily right angles.
Can a parallelogram have right angles?

+
Yes, a parallelogram with all right angles is specifically called a rectangle. However, not all parallelograms must have right angles; they can have any set of angles as long as opposite angles are equal and consecutive angles are supplementary.
Why is the area formula for a parallelogram so simple?

+
The area of a parallelogram is calculated by multiplying the base by the height because the shape can be “unfolded” into a rectangle of equal area. The height represents how far the parallelogram extends perpendicularly from one base to reach the other, making it a straightforward multiplication to find the area.