5 Tips for Mastering Product Rule of Exponents

In the world of algebra, understanding the product rule of exponents is fundamental for simplifying expressions and solving equations. This rule is essential for breaking down complex mathematical problems into manageable pieces. Here, we will explore five effective tips that can help you master the product rule of exponents, ensuring that you feel confident and well-equipped when tackling algebraic problems.
1. Understand the Basics

Before diving into the complexities, it’s crucial to understand the basic rule:
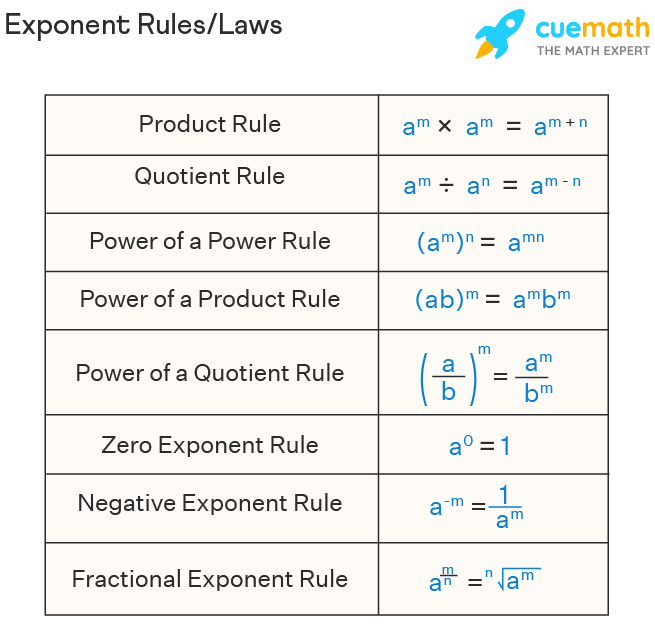
- When multiplying two exponential expressions with the same base, you add the exponents:
a^m × a^n = a^(m+n)This simple equation is the cornerstone of the product rule. Here’s an example:
3^2 × 3^4 = 3^(2+4) = 3^6✏️ Note: The base must be the same for this rule to apply. Different bases require different approaches.
2. Visualize the Concept

Visualization can be a powerful tool in learning. Consider the expression (5^3 × 5^2):
- 5^3 is like having three sets of 5:
- 5 × 5 × 5
- Now, 5^2 adds two more sets:
- 5 × 5 × 5 × 5 × 5
You now have 5 sets of 5, which translates to (5^(3+2) = 5^5).
3. Practice with Different Variables
To truly master the product rule, practice with different variables and exponents:
| Expression | Result |
|---|---|
| x^3 × x^5 | x^8 |
| y^4 × y^1 | y^5 |
| z^2 × z^3 | z^5 |

Practicing with different variables helps solidify the concept and ensures it’s not just a memorization task but an understanding one.
4. Handle Negative Exponents
The rule doesn’t change for negative exponents:
- a^(-m) × a^n = a^(n-m)
An example:
2^(-3) × 2^5 = 2^(5-3) = 2^2 = 4This extension of the rule can seem tricky, but it follows the same principles as with positive exponents.
5. Apply the Rule in Complex Expressions

Once you are comfortable with simpler cases, challenge yourself with more complex expressions. Here are some examples:
(3x^2 × 4x^3)^2 = (3 × 4 × x^(2+3))^2 = 12x^5- Understanding how to apply the product rule within complex expressions, especially those involving parentheses or variables with coefficients, can be a game-changer in problem-solving.
Moving forward from these basic tips, mastering the product rule of exponents is not just about learning a formula but understanding the underlying principles and practicing the application in various scenarios. This will not only enhance your ability to solve problems quickly but also deepen your appreciation for the beauty and logic of algebra.
With regular practice and a keen understanding, you'll find that algebraic expressions become more approachable, less intimidating, and sometimes even enjoyable to unravel. This mastery can lay the foundation for more advanced mathematical concepts where exponent rules are crucial. Remember, each time you successfully apply the product rule, you're not just simplifying an expression; you're reinforcing a deeper understanding of how numbers work together.
Why do we add exponents when multiplying?

+
When multiplying numbers with the same base, you’re essentially multiplying the same number multiple times. Adding the exponents counts how many times the base is being multiplied.
Can the product rule be used with different bases?

+
No, the product rule applies only to exponents with the same base. For different bases, you would use other methods like factoring or finding a common base if possible.
What if I have an expression with zero as an exponent?

+
Any number raised to the power of zero is equal to 1. Therefore, in the context of the product rule, if you encounter a zero exponent, treat it as 1.