Probability Worksheet Answer Key: Top 5 Insights

In the realm of mathematics education, probability plays a crucial role in shaping students' analytical skills, logical reasoning, and their ability to predict future events based on data. This segment of the curriculum can be both fascinating and daunting for learners. To facilitate understanding and provide clarity, probability worksheet answer keys become invaluable tools. Below, we explore the top five insights from a probability worksheet answer key, offering both teachers and students insights to enhance their learning journey.
Insight 1: Understanding the Basics

Before diving into complex scenarios, it’s vital to grasp the fundamental concepts of probability:
- Events and Outcomes: Events are collections of outcomes of an experiment, while outcomes are the possible results.
- Probability Definition: Probability is a measure of the likelihood that an event will occur, expressed as a number between 0 and 1.
- Basic Rules:
- If an event is certain, its probability is 1.
- If an event is impossible, its probability is 0.
🔔 Note: Understanding these basics helps in solving more advanced probability problems effectively.
Insight 2: The Role of Venn Diagrams in Probability
Venn diagrams are powerful visual tools in probability:
- They help in visualizing different sets or events and their intersections or unions.
- They simplify complex probability problems by showing the relationships between events.
| Scenario | Example |
|---|---|
| Two Separate Events | Choosing a red card or a heart from a deck of cards. |
| Overlapping Events | Choosing a king (which is also a face card) from a deck of cards. |
| Complementary Events | Not rolling a six on a die. |

🔍 Note: Venn diagrams aren't just for visual learners; they provide a structured way to calculate probabilities that can be universally appreciated.
Insight 3: Solving Probability with Tree Diagrams

Tree diagrams are instrumental when dealing with probabilities of sequential events:
- They break down the different possible outcomes in stages, making it easier to calculate combined probabilities.
- These diagrams illustrate both independent and dependent events.
Insight 4: Conditional Probability
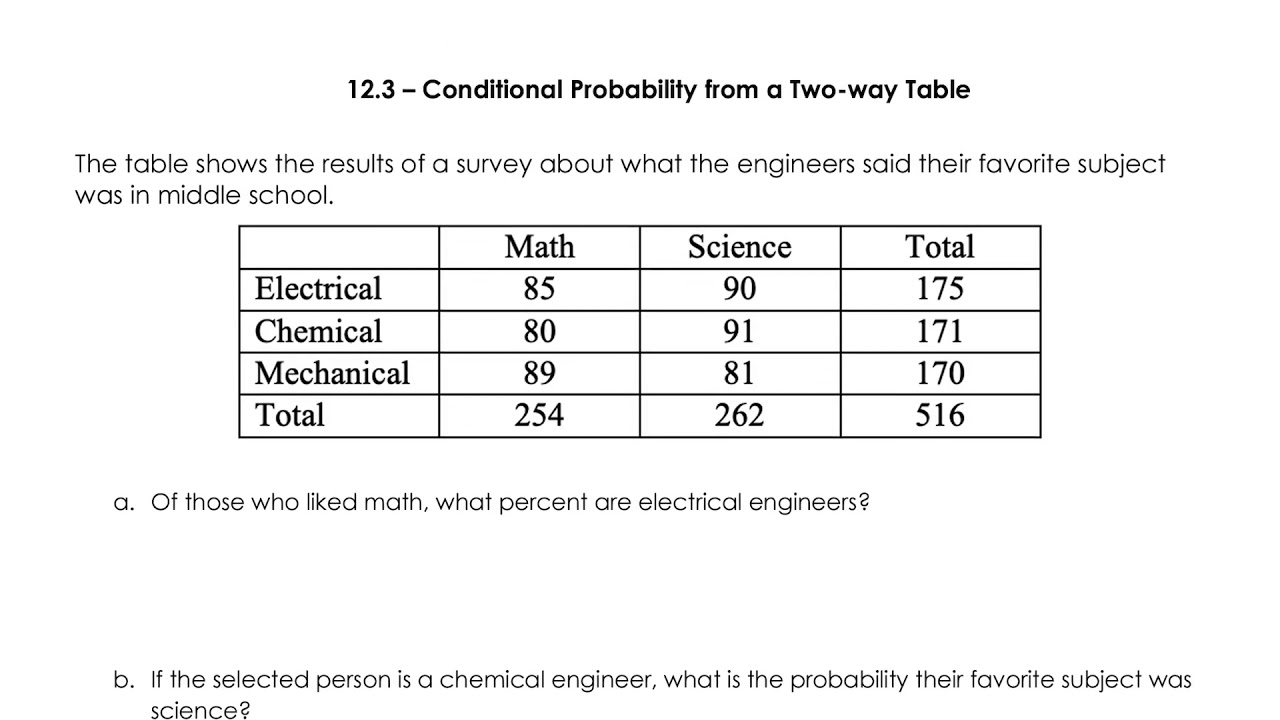
Conditional probability is a key concept where the likelihood of an event depends on another event having occurred:
- Bayes’ Theorem: This theorem helps in updating probabilities based on new information.
- The concept is critical in real-world applications like medical diagnostics, spam filtering, and machine learning.
📝 Note: Understanding conditional probability not only enriches the study of statistics but also has practical applications in various fields.
Insight 5: Probability Distributions

Moving from simple events to comprehensive data analysis, understanding probability distributions is essential:
- Discrete vs. Continuous: Probability distributions can be categorized as discrete, for finite or countable outcomes (e.g., number of heads in a coin toss), or continuous, where outcomes lie along a continuum (e.g., the height of individuals in a population).
- Key Distributions:
- Normal distribution, also known as the bell curve.
- Poisson distribution for events in a fixed interval.
- Binomial distribution for a set number of successes in a fixed number of trials.
By incorporating these insights into their teaching or learning approach, educators and students can transform what might seem like abstract numbers and theories into tangible, understandable concepts. The beauty of probability lies in its logical structure, which, when mastered, allows for better predictions, strategic planning, and informed decision-making in diverse areas of life. These insights are a roadmap to mastering probability, ensuring that learners not only remember formulas but understand the underlying concepts and their applications.
What are the benefits of using probability in real life?

+
Probability helps in making informed decisions in various fields like finance, insurance, sports analytics, and even daily life activities like weather prediction or gambling.
Can probability problems be solved without diagrams?

+
Yes, while diagrams like Venn and tree diagrams are helpful, probability can be calculated using mathematical formulas alone. However, visual aids often make the process clearer and less error-prone.
How do conditional probabilities influence our daily lives?

+
Conditional probabilities impact daily decisions, such as estimating the likelihood of an event given that another event has already occurred. This is seen in scenarios like traffic routing based on current congestion, weather predictions based on current conditions, or personalized recommendations on streaming platforms.