Probability Worksheet: Independent vs Dependent Events

In mathematics, understanding the difference between independent and dependent events is crucial, especially when dealing with probability. Let's dive into these concepts to not only clarify their definitions but also to understand their implications in real-world scenarios and calculations.
Defining Independent and Dependent Events

Before we explore these types of events further, let's define what they are:
- Independent Events: These are events where the occurrence or non-occurrence of one event does not affect the probability of the other event. For example, rolling a die and then flipping a coin are independent events since the outcome of the die roll does not influence the result of the coin toss.
- Dependent Events: These events occur when the outcome of one event influences the probability of another event. If you draw a card from a deck without replacement, the probability of the second card being of a certain type changes based on what card was drawn first.
Examples to Illustrate the Differences

To better grasp the distinction, let's look at some examples:
Independent Events

- Spinning a Spinner: If you spin a spinner and it lands on red, the probability of spinning a red again remains the same.
- Drawing from Multiple Decks: If you draw cards from different decks, each draw is independent of the previous one since the cards are not shared.
Dependent Events
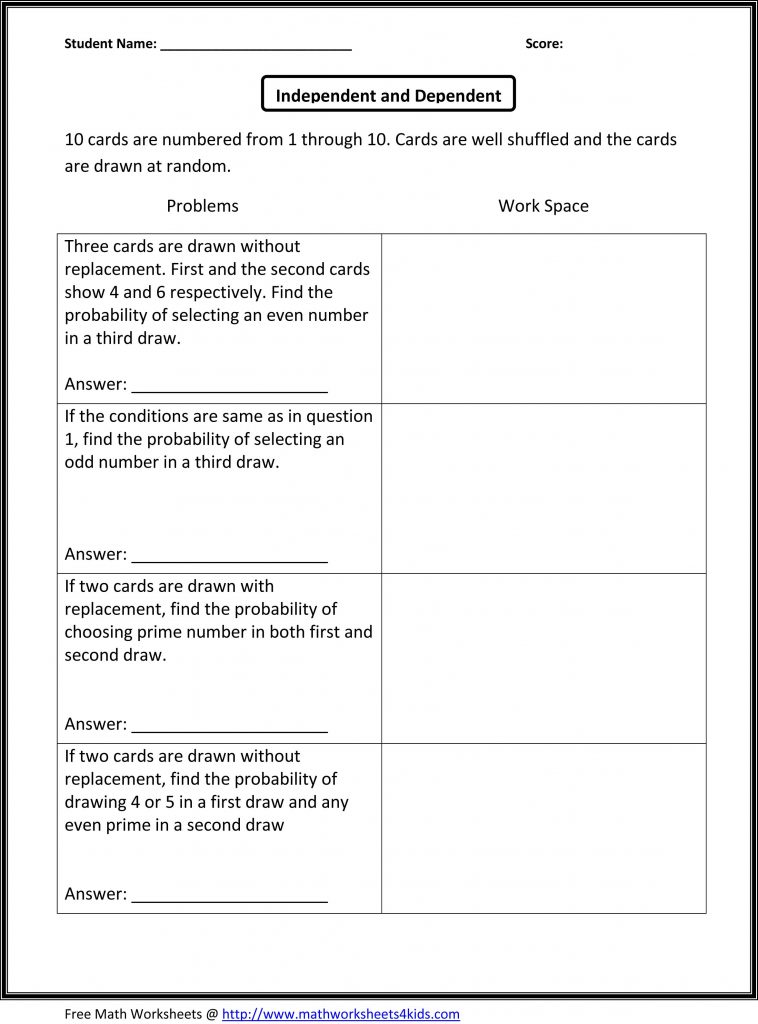
- Drawing without Replacement: If you draw a red card from a standard deck, the probability of drawing another red card next is now higher because there are fewer black cards left.
- Weather Forecast: If it rains today, the likelihood of it raining tomorrow might be increased due to weather patterns, making these events dependent.
Calculating Probability in Independent and Dependent Events

Let's see how you calculate probabilities for both types of events:
Probability of Independent Events

The probability of two independent events both happening is the product of their individual probabilities:
P(A ∩ B) = P(A) * P(B)
🔑 Note: Here, ∩ denotes the intersection of the events, meaning both events happen together.
Probability of Dependent Events

When events are dependent, we need to adjust for the altered probability after the first event:
P(A ∩ B) = P(A) * P(B|A)
Here, P(B|A) is the conditional probability of B given that A has occurred.
Worksheet Exercises

Let's apply what we've learned with some exercises:
| Scenario | Question | Calculation |
|---|---|---|
| Independent Events | What's the probability of flipping two coins and getting heads on both? | (1/2) * (1/2) = 1/4 |
| Dependent Events | From a deck, draw a card, then another. What’s the probability of both being hearts? | (13/52) * (12/51) ≈ 0.0588 |

Real-World Applications

Understanding these concepts isn't just about academic interest:
Business and Marketing

- Customer Behavior: Knowing if buying decisions are independent or dependent can affect how products are marketed.
Gambling

- Casino Games: Understanding the independence or dependence of game outcomes helps in formulating betting strategies.
Health Research

- Epidemiology: Studying whether events like getting a flu shot and contracting the flu are independent can guide public health strategies.
The concept of independent and dependent events is foundational not only in probability theory but also in its application to real-life situations. By understanding these events, we can make more informed decisions in various fields from business to health care, enhancing our analytical skills and ability to predict outcomes. This understanding can lead to better strategies in gambling, more effective marketing campaigns, and improved public health policies.
What makes events independent in probability?

+
Events are independent if the occurrence of one does not affect the probability of the other event happening.
How does dependent probability work?

+
In dependent events, the outcome of the first event changes the probability of the subsequent event because they are interconnected.
Can weather events be dependent?

+
Yes, weather events can be dependent. For instance, the likelihood of rain tomorrow might be higher if it rained today due to atmospheric conditions.
Why is understanding event dependency important?
+Understanding event dependency allows for better predictions, decision-making, and strategy formulation in various fields.
Can events be both dependent and independent at the same time?
+No, an event is either dependent or independent, not both at the same time. However, different sets of events can have varying relationships with each other.