3 Ways to Master Special Right Triangles Easily

In the realm of geometry, triangles are fundamental shapes that offer a wealth of interesting properties and relationships. Among these, special right triangles hold a particular fascination due to their unique ratios and applications in solving various mathematical and real-world problems. If you're looking to master special right triangles, here are three effective strategies that can help you understand and utilize these geometrical gems with ease:
Understanding the Basics of Special Right Triangles

Before diving into the methods of mastering special right triangles, it should be beneficial to refresh your knowledge on what these triangles are:
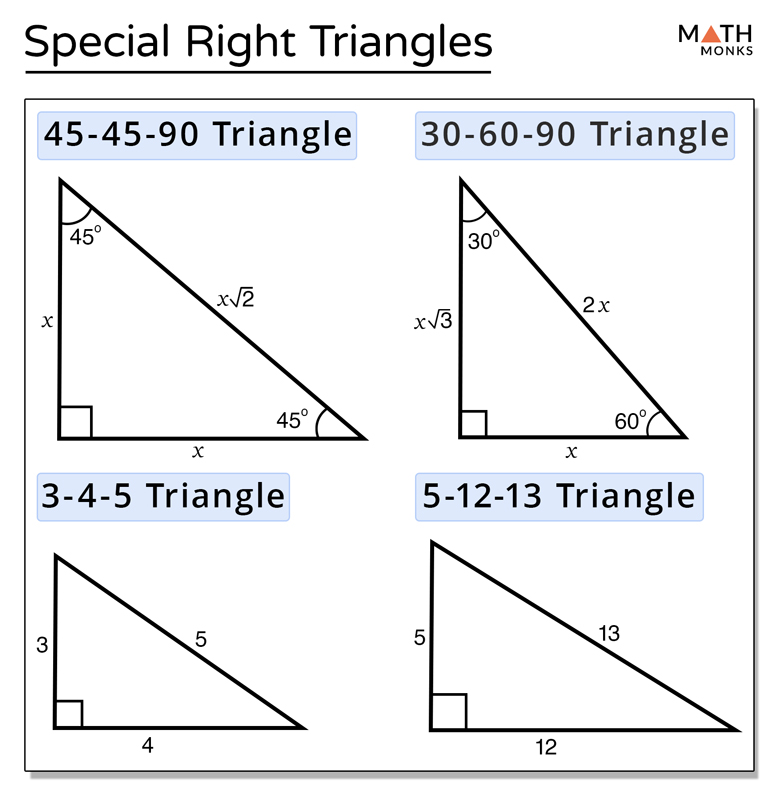
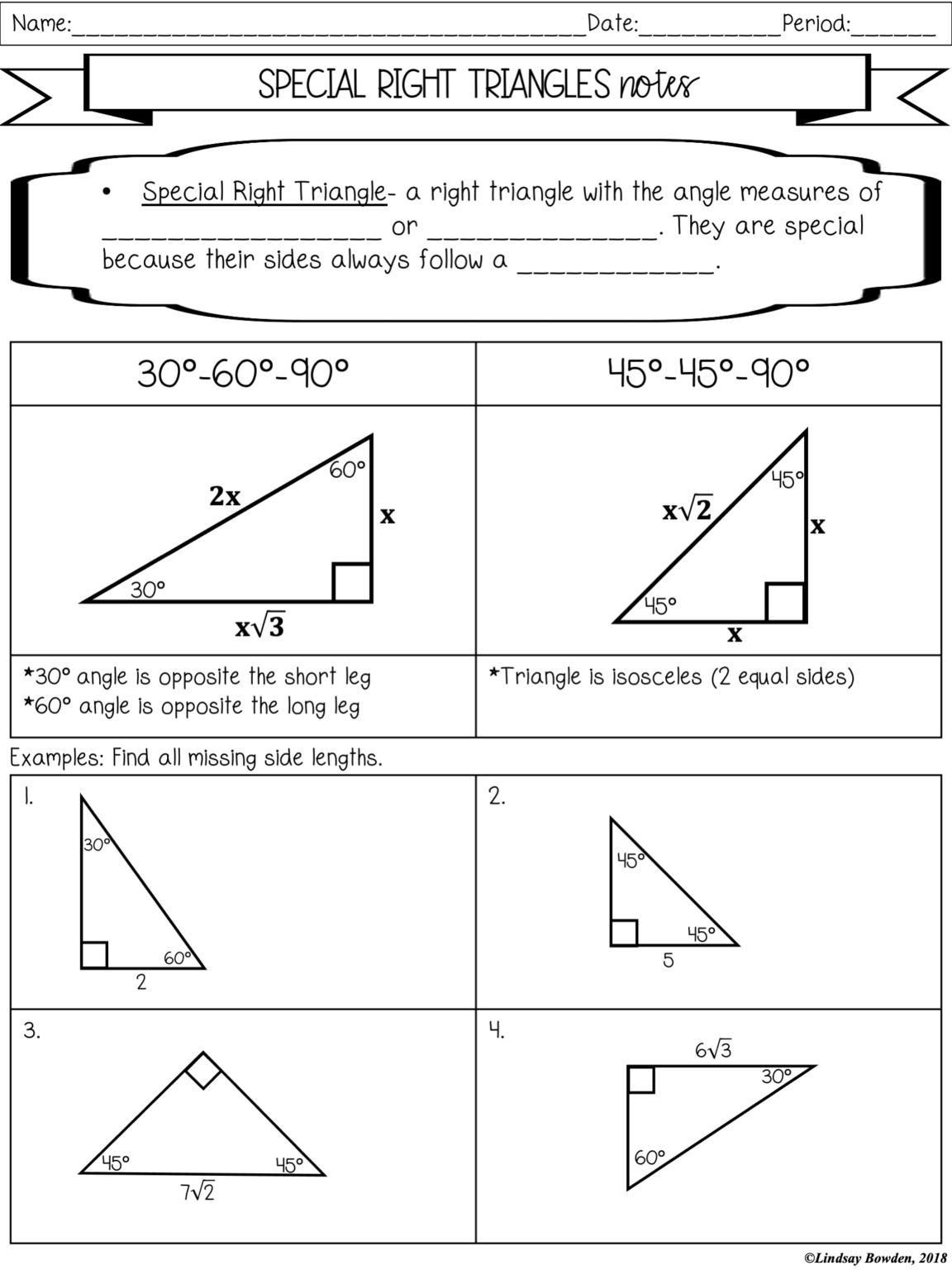
- 30-60-90 Triangle: This triangle has angles of 30°, 60°, and 90°. The sides are in the ratio 1:√3:2, where the hypotenuse is twice the length of the shortest leg.
- 45-45-90 Triangle: With two angles of 45° each and a right angle, the triangle's sides are in the ratio 1:1:√2. Here, the legs are of equal length, and the hypotenuse is the leg's length multiplied by √2.
1. Visualize with Geometry Software

One of the best ways to internalize the properties of special right triangles is to visualize them. Here’s how:
- Create Interactive Models: Use software like GeoGebra, Desmos, or other educational geometry tools to create models of these triangles. You can dynamically adjust angles to see how the triangle's properties change.
- Observe Changes: Watch how the side lengths maintain their unique ratios when you alter the triangles. This visualization helps in understanding the practical application of these ratios.
- Problem Solving: Utilize the software to solve problems. For instance, if one side is known, use the tools to automatically calculate others, providing instant feedback.
2. Employ Mnemonics and Memory Aids
Special right triangles have unique ratios which can be remembered using mnemonics:
- For 45-45-90: Think "Double it for the hypotenuse." If one leg is x, the hypotenuse is x√2.
- For 30-60-90: "The short side, long side, and the roof." If the shortest side is x, the hypotenuse (the 'roof') is 2x, and the longest side is x√3.
Create your own mnemonics or rhymes that help you remember the ratios. Here’s a simple table to illustrate:
| Triangle | Angles | Side Lengths |
|---|---|---|
| 45-45-90 | 45°, 45°, 90° | 1, 1, √2 |
| 30-60-90 | 30°, 60°, 90° | 1, √3, 2 |

3. Practice with Real-World Applications

Theoretical knowledge becomes solid when applied to real-world scenarios. Here’s how you can practice:
- Elevation and Depression: Use special right triangles in problems involving angles of elevation or depression, like calculating the height of a tree or the depth of a well.
- Navigation and Mapping: Apply these triangles when working with topographic maps or in navigation problems where right triangles occur naturally.
- Physics and Engineering: In physics, special right triangles can help in resolving forces or vectors; in engineering, they appear in the design of structures.
📝 Note: When applying special right triangles in real-world problems, it's useful to first sketch the situation to visualize which triangle fits best.
Mastering Through Repetition

Practice is key in mastering any subject, but with mathematics, and particularly geometry, repetition with variation is crucial:
- Work on Problems: Solve as many problems as you can find related to special right triangles. Use textbooks, online resources, or even create your own problems.
- Mix it up: Don't just repeat the same types of problems. Try to mix angle measures, side lengths, and the context in which the triangles are used.
By using these strategies, you can make special right triangles less of a mystery and more of a mathematical friend. Understanding these triangles not only enhances your ability to solve geometric problems but also serves as a fundamental building block for higher mathematics and practical applications in fields like physics, engineering, and architecture.
Why are special right triangles important?

+
Special right triangles simplify the calculation of angles and side lengths in various mathematical and real-world scenarios, making problem-solving more efficient.
Can I use any other formulas to find angles in a special right triangle?

+
While the ratios provided are the simplest, trigonometric functions like sine, cosine, and tangent can also be used, though they tend to be more complex for these particular triangles.
What’s the difference between a regular right triangle and a special right triangle?
+
Special right triangles have specific angle measures and side length ratios (30-60-90 and 45-45-90), whereas regular right triangles do not adhere to these fixed properties, making them more versatile but harder to calculate without additional information.



