Graphing Radical Functions Worksheet Answer Key Revealed
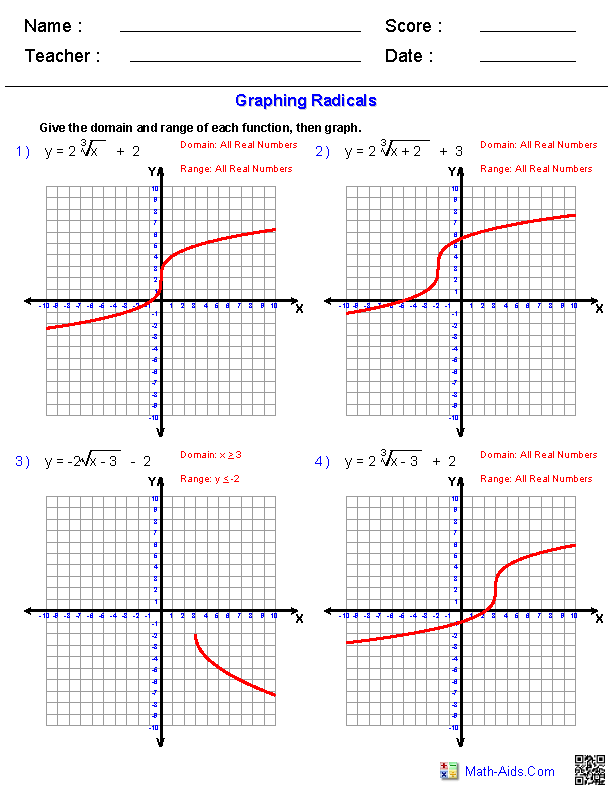
Mastering the Art of Graphing Radical Functions: A Comprehensive Guide
Radical functions represent a unique branch of algebra that many students often find perplexing due to their non-standard shape and transformations. Understanding how to graph these functions not only helps in solving specific types of problems but also deepens your mathematical comprehension. In this detailed guide, we'll delve into graphing radical functions, emphasizing practical applications, key concepts, and providing an answer key for a popular graphing radical functions worksheet.
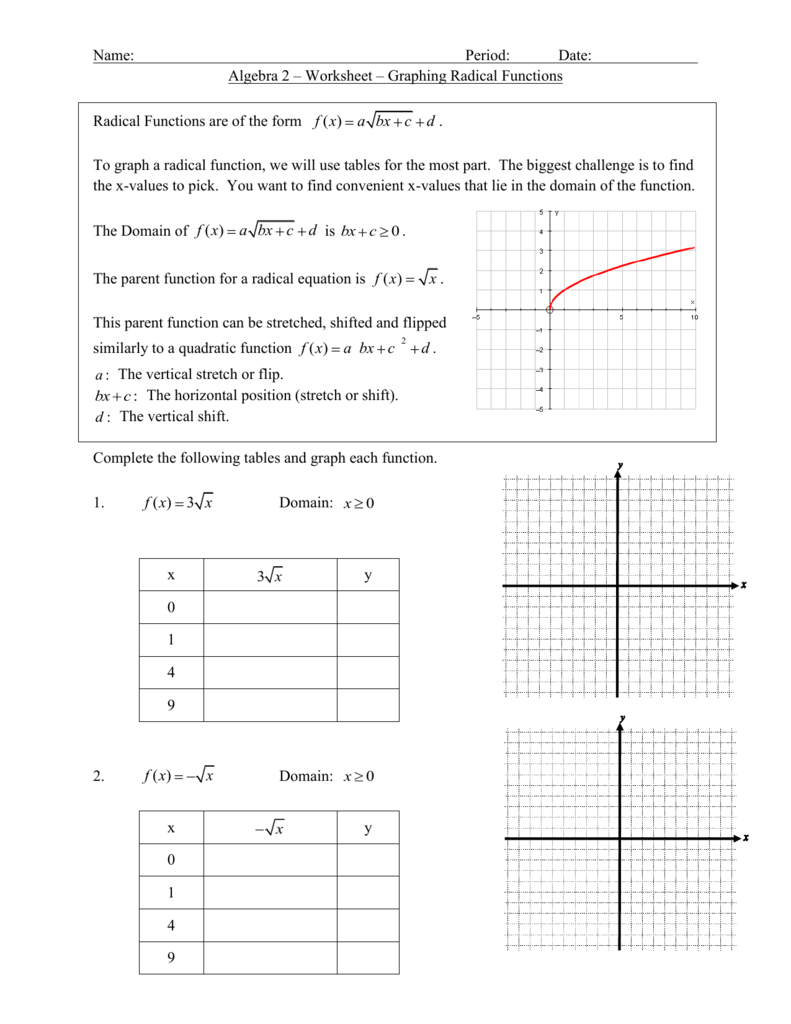
Introduction to Radical Functions

Radical functions are equations where the dependent variable (y) is under a radical sign. The most common form is:
- Square Root Function: ( y = \sqrt{x} )
- Cube Root Function: ( y = \sqrt[3]{x} )
These functions can also include coefficients, shifts, and reflections, altering the graph in various ways.
Graphing Square Root Functions
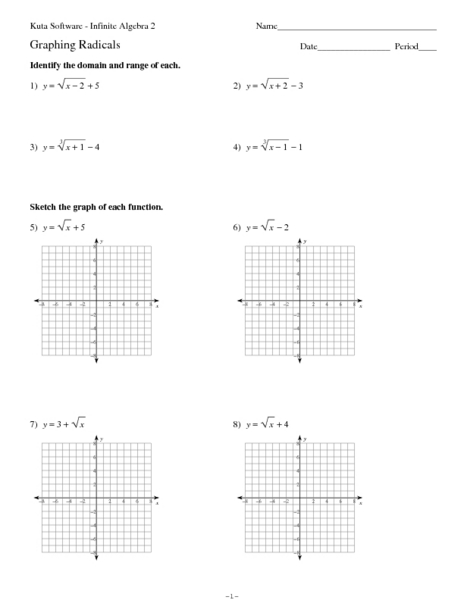
Let’s start with the graph of ( y = \sqrt{x} ):
- The domain of ( y = \sqrt{x} ) is ( x \geq 0 ).
- The range is ( y \geq 0 ).
- The function increases but at a decreasing rate.
- The graph starts at the origin and curves away from the x-axis as x increases.
Here is how you graph ( y = \sqrt{x} ):
- Identify key points:
- At ( x = 0, y = 0 ).
- At ( x = 1, y = 1 ).
- At ( x = 4, y = 2 ).
- Plot these points and sketch the curve to connect them smoothly.

Transformations of Square Root Functions

Understanding how transformations affect the graph of ( y = \sqrt{x} ) is crucial:
- Vertical Shift: ( y = \sqrt{x} + k )
- Horizontal Shift: ( y = \sqrt{x - h} )
- Reflection: ( y = -\sqrt{x} ) reflects over the x-axis, ( y = \sqrt{-x} ) reflects over the y-axis.
- Vertical Stretch/Compression: ( y = a\sqrt{x} )
- Horizontal Stretch/Compression: ( y = \sqrt{bx} )
These transformations allow you to modify the graph systematically, changing its position, shape, and orientation.
Graphing Cube Root Functions
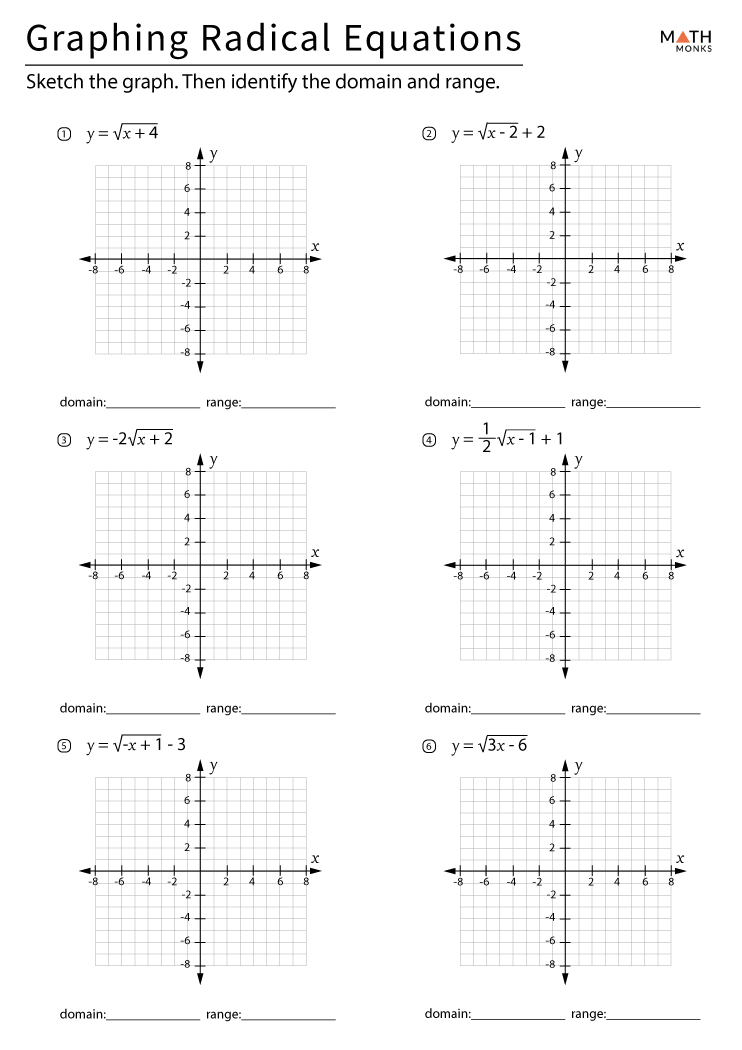
The graph of ( y = \sqrt[3]{x} ):
- Domain and range are all real numbers.
- It passes through the origin and has symmetry about the origin.
- The function is increasing, but it becomes more gradual as x increases or decreases.
To graph:
- Identify key points:
- At ( x = -1, y = -1 ).
- At ( x = 0, y = 0 ).
- At ( x = 1, y = 1 ).
- Plot these points and sketch the curve to connect them smoothly.

Worksheet Answer Key for Graphing Radical Functions
| Function | Graph Description | Key Points |
|---|---|---|
| ( y = \sqrt{x} ) | Starts at (0,0), curves away from x-axis | (0,0), (1,1), (4,2) |
| ( y = \sqrt{x-2} ) | Shifts 2 units right, starts at (2,0) | (2,0), (3,1), (6,2) |
| ( y = 2\sqrt{x} ) | Stretches vertically by factor 2 | (0,0), (1,2), (4,4) |
| ( y = \sqrt[3]{x} ) | Passes through origin, symmetrical | (-1,-1), (0,0), (1,1) |
| ( y = -\sqrt[3]{x} ) | Reflection of ( y = \sqrt[3]{x} ) | (-1,1), (0,0), (1,-1) |

📌 Note: When plotting transformed functions, consider how each transformation affects the key points of the original function.
By now, you've gained insights into graphing both square and cube root functions, understanding how transformations alter these graphs, and applied your knowledge to a specific worksheet. Remember, practice is key to mastering these concepts. Here are a few additional tips for success:
- Practice sketching various radical functions until transformations become intuitive.
- Use graphing software or a graphing calculator to verify your manual plots.
- Understand how the coefficients and constants in radical functions influence the graph's behavior.
The beauty of algebra lies in how these abstract functions reveal themselves graphically, providing a visual interpretation of algebraic expressions. The journey from recognizing basic shapes to manipulating them through transformations not only prepares you for more complex mathematical challenges but also enhances your problem-solving skills. Keep exploring, and with each graph you plot, you'll find yourself more proficient in the language of mathematics.
How can I determine the domain and range of a radical function?

+
For square root functions, the domain starts where the expression inside the square root is non-negative. For cube root functions, both domain and range are all real numbers because the cube root of any real number is defined.
What is the difference between a square root and cube root function?

+
A square root function only yields non-negative outputs due to the square root operation, whereas a cube root function can yield both positive and negative values, providing symmetry about the origin.
Can radical functions be negative?

+
No, square root functions yield non-negative values. However, cube root functions and higher odd root functions can be both positive and negative.