Master Linear Equations with Free Worksheets Today!

Understanding linear equations is foundational in mathematics, serving as the bedrock for many advanced mathematical concepts and applications in real-world problems. This blog post aims to delve deep into linear equations, providing you with not just an understanding but practical tools in the form of free worksheets to master this critical area of algebra.
Why Master Linear Equations?

Linear equations, often expressed in the form (Ax + By = C), where (A), (B), and (C) are constants, are essential for several reasons:
- They form the foundation for graphing linear functions.
- Linear equations are used in calculus to solve problems involving rates of change.
- They are crucial in business for cost analysis, profit calculation, and linear programming.
Mastering linear equations not only makes you proficient in algebra but also sharpens your analytical thinking, problem-solving abilities, and opens doors to advanced mathematical and scientific studies.
Understanding Linear Equations

A linear equation in one variable, like (2x + 3 = 9), involves finding the value of (x) that makes the equation true. Here are the key steps to solve such equations:
- Isolate the Variable: Move all terms involving (x) to one side of the equation and constants to the other.
- Perform Inverse Operations: Use operations like addition, subtraction, multiplication, or division to isolate (x).
- Verify the Solution: Substitute your solution back into the original equation to ensure it satisfies the equation.
📝 Note: Always check your work by substituting the solution back into the equation to ensure you've found the correct value for x.
Two-Variable Linear Equations

When dealing with two variables, such as (y = 3x + 5), you’re often looking to find the relationship between (x) and (y). Here’s how to interpret such equations:
- Slope-Intercept Form: (y = mx + b) where (m) is the slope (gradient) and (b) is the y-intercept. Here, 3 is the slope, meaning (y) increases by 3 for every increase in (x) by 1, starting from 5 when (x) is 0.
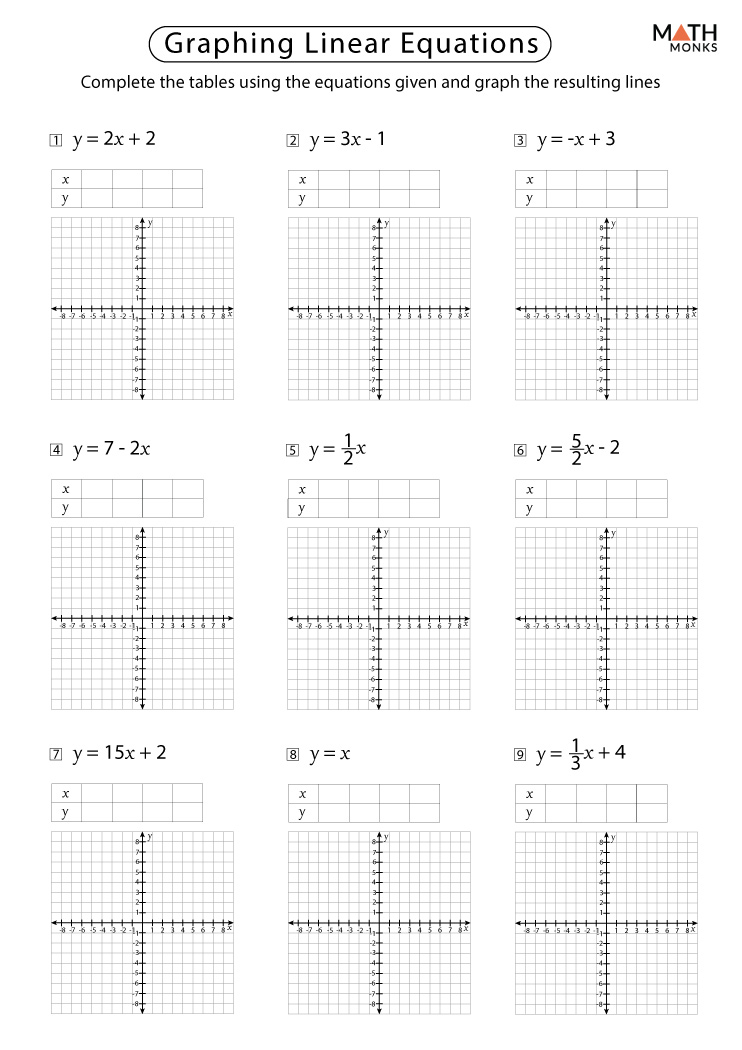
- Graphing: You can graph these equations by plotting the y-intercept and then using the slope to find additional points on the line.
| Form of Linear Equation | Description |
|---|---|
| Standard Form | Given as Ax + By = C. Useful when solving systems of equations. |
| Slope-Intercept Form | Given as y = mx + b. Best for understanding the line's slope and y-intercept. |

🔍 Note: The slope in the slope-intercept form tells you how steep the line is. A higher slope means a steeper line.
Solving Systems of Linear Equations

Solving systems of linear equations involves finding values of (x) and (y) (or more variables) that satisfy all equations simultaneously. Here are three common methods:
- Substitution Method: Solve one equation for one variable and substitute into the other.
- Elimination Method: Add or subtract equations to eliminate one of the variables.
- Graphing Method: Plot the equations and find the intersection point.
🧠 Note: The graphing method can be very visual but less precise for exact solutions. Use it for understanding but consider algebraic methods for accuracy.
Practice Makes Perfect: Free Worksheets

To truly master linear equations, practice is essential. Here are some ways to utilize free worksheets:
- Download worksheets that cover different types of linear equations.
- Practice solving both one-variable and two-variable equations.
- Use worksheets that include word problems to apply equations to real-life scenarios.
📚 Note: Regular practice not only helps in memorizing steps but also in improving problem-solving speed and accuracy.
As we wrap up this comprehensive guide on linear equations, remember that the journey of mastering algebra begins with understanding these simple yet powerful expressions. They form the core of many mathematical and real-world applications. With consistent practice through the use of free worksheets, you can develop a deep understanding and proficiency in solving linear equations. Not only will this knowledge serve as a stepping stone to more complex mathematical topics, but it will also enhance your logical reasoning skills, making you more adept at tackling mathematical challenges in diverse fields.
What is the best method to learn linear equations?

+
The best method involves a combination of understanding the theory, practicing with worksheets, and applying equations to real-life problems. Practice and application are key.
How do I check if my solution to a linear equation is correct?

+
Substitute your solution back into the original equation. If both sides of the equation are equal, then your solution is correct.
Can linear equations always be solved?

+
Linear equations with one variable typically have one solution. Two-variable equations can have no solution, one solution, or infinitely many solutions depending on the situation.