Master Geometry Proofs: Free Practice Worksheet
Geometry is a cornerstone of mathematical education, providing a window into the logical, structured world of shapes, angles, and dimensions. Among its many fascinating topics, geometry proofs stand out as both challenging and rewarding. They require not just understanding of concepts but the ability to apply logic in a rigorous manner. This post will guide you through mastering geometry proofs with a comprehensive practice worksheet, tips for success, and an understanding of why proofs are so crucial in your mathematical journey.
Why Geometry Proofs Matter

Geometry proofs are not just exercises in logical deduction; they are essential for several reasons:
- Developing Logical Thinking: Proofs force you to reason sequentially, ensuring each step follows logically from the previous one.
- Reinforcing Concepts: The act of proving a theorem deepens your understanding of geometric principles, making them more than just abstract concepts.
- Problem Solving: They enhance your problem-solving skills by requiring you to approach problems from different angles.
- Higher Mathematics Preparation: Proofs are the bedrock of advanced mathematics, preparing you for fields like topology, calculus, and abstract algebra.
📝 Note: Proficiency in geometry proofs can significantly improve your mathematical intelligence and boost your confidence in tackling complex problems.
Understanding Geometry Proofs

A proof in geometry is a logical argument that establishes the truth of a geometric statement. Here’s what you need to know:
- Given Information: Start with given facts or hypotheses.
- Statements: Each line of the proof includes a statement to be proved.
- Reasons: Corresponding to each statement, there must be a reason from axioms, definitions, postulates, or previously proved theorems.
- Logical Deduction: Statements are deduced from previous ones using logical reasoning.
Components of a Geometry Proof

To craft a solid geometry proof, understand these key components:
| Component | Description |
|---|---|
| Given | Facts or hypotheses provided at the beginning of the problem. |
| Prove | The statement that needs to be proved true. |
| Diagram | A visual representation that helps visualize the problem and often provides additional information. |
| Statements | Logical assertions in the proof. |
| Reasons | The logical basis for each statement, derived from axioms or other previously established truths. |

How to Master Geometry Proofs

Here are steps to improve your proficiency in writing geometry proofs:
1. Understand Basic Concepts

Before diving into proofs, ensure you have a firm grasp on basic geometric principles such as:
- Angles (types, properties)
- Triangles (types, congruence, similarity)
- Circles (chords, arcs, tangents)
- Parallel lines and their properties
Mastery of these will provide the foundation for more complex proofs.
2. Analyze Past Proofs

Look at proofs of well-known theorems. Deconstruct them:
- Identify the given information.
- Trace the logical progression of statements and reasons.
- Understand the use of specific geometric properties or theorems in the proof.
👓 Note: This exercise not only enhances your understanding but also helps in recognizing patterns and common proof strategies.
3. Practice Proof Writing

Here are some techniques to practice:
- Two-Column Proofs: Practice writing proofs in two columns where one side lists statements, and the other lists the reasons for each statement.
- Proof Strategies: Learn common proof strategies like direct proof, contradiction, or contrapositive.
- Start with Simple Proofs: Begin with simpler proofs like proving two angles are congruent or triangles are similar.
4. Use Geometry Proof Worksheets

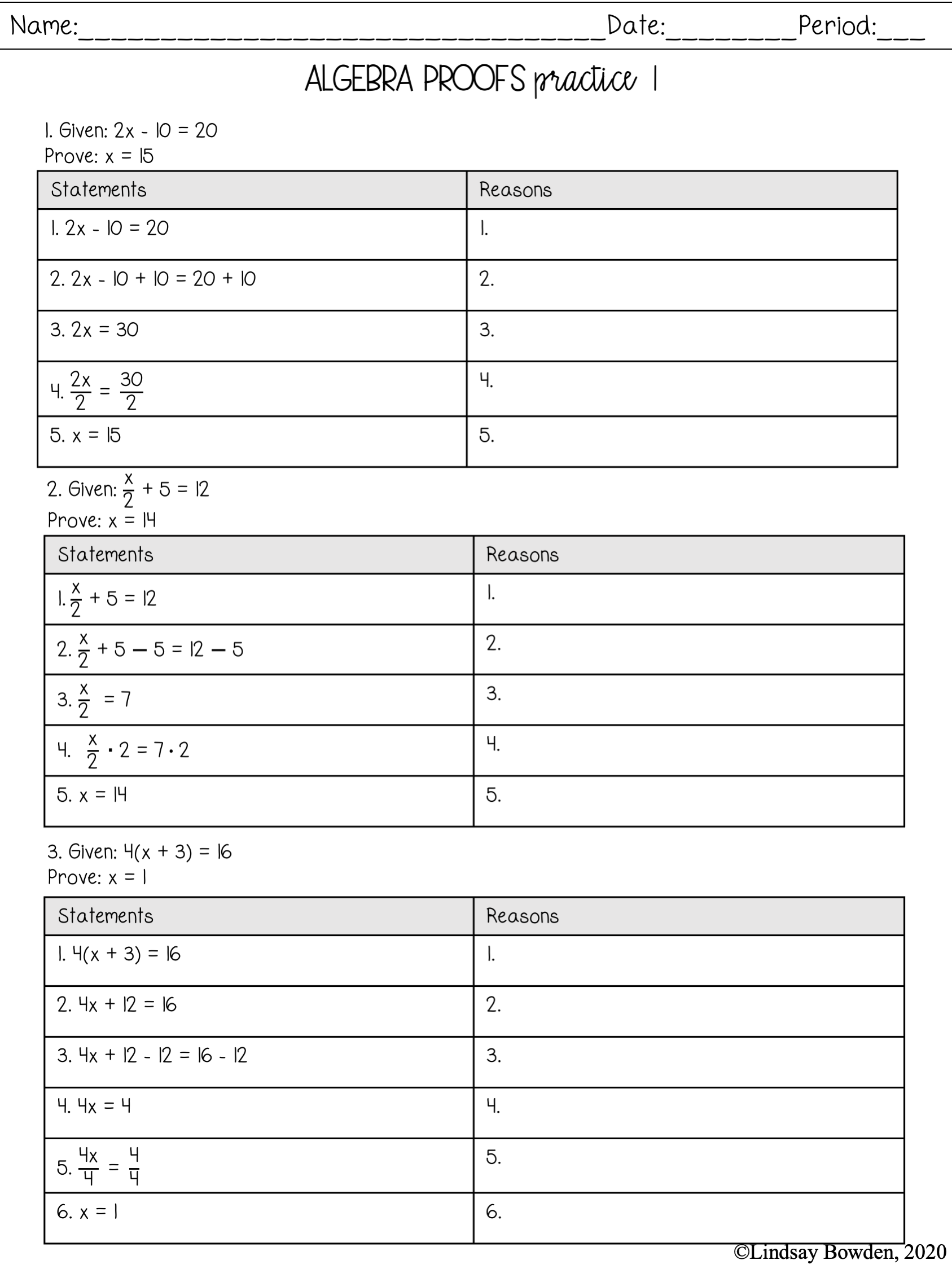
Below is a free geometry proofs practice worksheet designed to help you hone your skills:
🌟 Note: Download and print this worksheet for offline practice, or work through it online to refine your proof-writing abilities.
5. Review and Reflect

After completing proofs, take time to:
- Review your work for any logical errors.
- Reflect on the strategies used.
- Consider alternative methods to solve the same problem.
Common Pitfalls in Writing Geometry Proofs

Here are some mistakes to avoid:
- Not Labeling Diagrams: Always label diagrams completely; missing labels can lead to errors.
- Misinterpreting Given Information: Pay close attention to the information provided to ensure you don’t miss or misinterpret key facts.
- Lack of Clarity: Each statement should be clear, concise, and logically connected to the previous one.
- Overlooking Simple Proofs: Sometimes, the simplest proofs require the most clarity in reasoning.
Expanding Your Geometry Proficiency

Once comfortable with basic proofs, consider these advanced topics:
1. Advanced Proof Techniques

- Coordinate Geometry Proofs: Incorporate coordinate systems for proofs involving slopes, midpoints, and distances.
- Vector Geometry: Explore proofs using vectors, which can simplify complex geometric relationships.
2. Proofs in Real-World Applications

Understand how geometric proofs apply to real-life problems:
- Surveying: Proving properties of land for survey calculations.
- Architecture: Ensuring structural integrity and design accuracy.
- Computer Graphics: Proving relationships between shapes for rendering and animation.
Conclusion

Mastering geometry proofs is not just about solving mathematical problems; it’s about cultivating a mindset of logical reasoning, problem-solving, and critical thinking. By working through this free geometry proofs practice worksheet, you’ve embarked on a path to enhance these skills significantly. Remember, proofs are not only about proving what is true but also understanding why it is true. This knowledge equips you to handle not just the known problems but also the unknowns that lie ahead in your mathematical journey.
How often should I practice geometry proofs?

+
Regular practice is key. Aim for at least once a week to keep your skills sharp and continuously improve.
What are some common mistakes when writing geometry proofs?

+
Common mistakes include assuming what you need to prove, failing to fully label diagrams, and using illogical or incorrect reasoning. Always review your work carefully.
Why do proofs take so long to solve?

+
Proofs require careful logical thinking and often involve multiple steps. They demand precision, and taking time ensures accuracy in your reasoning.