5 Essential Tips for Polynomial Long Division Practice

Mastering polynomial long division might seem daunting initially, but with the right approach, this foundational algebraic skill becomes an invaluable tool for simplifying expressions and solving complex equations. Here are five crucial tips to enhance your practice and proficiency in polynomial long division.
Understand the Concept of Division
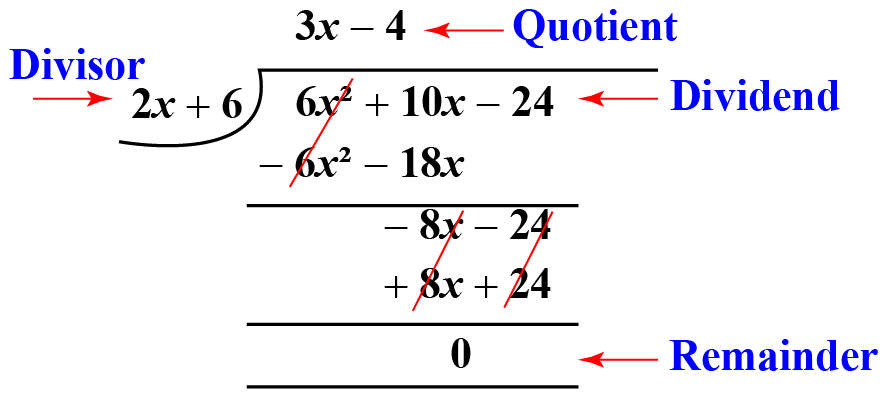
Before you dive into polynomial long division, it’s essential to grasp the basic concept of division. Division in algebra functions similarly to that in arithmetic, but instead of numbers, you’re dealing with variables and terms. Here’s how:
- Identify the terms: Just like in numeric division where you consider how many times the divisor goes into the dividend, identify the highest degree terms of the polynomials.
- Divide term by term: Divide the leading term of the dividend by the leading term of the divisor to get the first term of the quotient.
- Multiply and subtract: Multiply this term by the divisor, then subtract it from the original polynomial to find the next remainder.
💡 Note: Understanding the fundamental arithmetic principle behind polynomial division helps in visualizing the process and applying it accurately.
Set Up Your Division Properly

The setup is pivotal in polynomial long division. Here’s how to ensure you start correctly:
- Write out the polynomials: Arrange your dividend and divisor in descending order of degree. If any terms are missing, include them with a coefficient of zero to maintain consistency.
- Label your problem: Put the dividend inside a long division symbol, and the divisor to the left, as in:
) dividend divisor 
- Follow the standard algorithm: Begin dividing the highest degree term in the dividend by the highest degree term in the divisor.
⚙️ Note: An incorrect setup can lead to errors in your division process. Take the time to ensure everything is aligned correctly.
Practice Makes Perfect

There’s no better substitute for practice when mastering polynomial long division. Here are ways to enhance your practice sessions:
- Use varying complexity: Start with simple polynomials and gradually increase the complexity. This helps build confidence in the method.
- Work with different coefficients and terms: Practicing with polynomials that have fractional coefficients or variables can improve your fluency in handling complex problems.
- Time yourself: Gradually work towards completing divisions within a time limit to improve speed and accuracy.
👍 Note: Consistent practice not only solidifies your understanding but also increases your speed and reduces errors during calculations.
Check Your Work
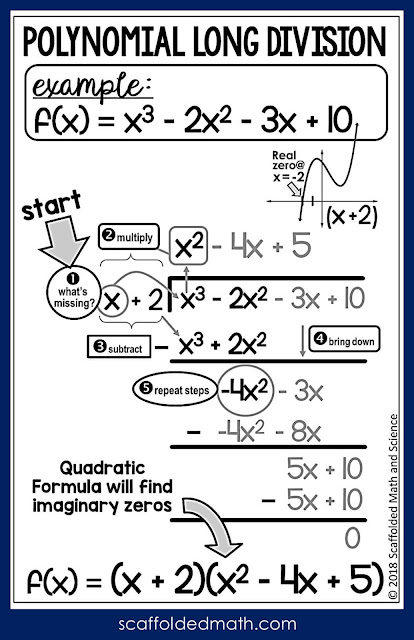
One of the most beneficial habits in polynomial long division is to always verify your results. Here are some methods to check your work:
- Re-substitution: Multiply the quotient by the divisor and add the remainder to see if it equals the original dividend.
- Use Remainder Theorem: Substitute any value into your polynomials and check if the remainders match.
- Graphical Verification: Use graphing software to plot both the original polynomial and your reconstructed one using the quotient and remainder.
Learn from Your Mistakes

Mistakes are integral to the learning process. Here’s how to turn errors into learning opportunities:
- Analyze errors: When you make a mistake, go back through each step to understand where and why the error occurred.
- Review frequently: Regularly go over previous practice problems, focusing on those where you made mistakes, to strengthen your understanding.
- Ask for feedback: If possible, have a teacher or tutor review your work to provide insights on common pitfalls.
In conclusion, mastering polynomial long division involves understanding the fundamentals, practicing with intention, and learning from your mistakes. By incorporating these tips into your study routine, you not only enhance your ability to perform polynomial long division but also improve your overall algebraic skills. Remember, proficiency in polynomial long division can unlock doors to further advanced topics in mathematics, making this skill a cornerstone for future learning.
Why is it important to practice polynomial long division?

+
Practicing polynomial long division is crucial because it:
- Improves your ability to solve complex equations and simplify expressions.
- Develops problem-solving skills and mathematical fluency.
- Prepares you for more advanced algebraic concepts and applications in calculus.
What do I do if I get stuck in the division process?

+
If you get stuck, consider:
- Rechecking your setup and division steps.
- Using synthetic division as an alternative method for simpler polynomials.
- Walking through the process with a simpler problem to refresh your understanding.
How can I make polynomial long division easier?

+
To make polynomial long division easier:
- Practice regularly to increase familiarity with the process.
- Understand the significance of each step in the division process.
- Focus on setting up the problem correctly and keep a consistent rhythm as you go through the steps.