Mastering Polygons on Coordinate Plane: Printable Worksheet

Polygons, with their straight sides and angular vertices, have been fundamental in the world of geometry for centuries. Whether it's a humble square, a steadfast triangle, or a more complex shape like a nonagon, each offers a unique challenge to the learner's mind. In this detailed guide, we will delve deep into understanding these geometric figures through the lens of the coordinate plane, offering practical exercises, insightful explanations, and a printable worksheet to solidify your grasp on this topic.
Understanding the Coordinate Plane

The coordinate plane, a two-dimensional system formed by a horizontal x-axis and a vertical y-axis, is the playground for plotting shapes. The intersection of these axes, known as the origin, has coordinates (0,0). Points on this plane are defined by pairs of coordinates (x,y), where x represents the horizontal position, and y denotes the vertical. Here’s how we can represent the basic polygons:
- Triangle: A simple three-sided figure. When plotted on the coordinate plane, the vertices of a triangle can be identified by three distinct points.
- Quadrilateral: A four-sided polygon can range from the square with all sides equal and all right angles to a kite with two pairs of equal-length adjacent sides.
- Hexagon: Six-sided figures are often encountered in real life, from the cells in a honeycomb to the stop sign you see daily.
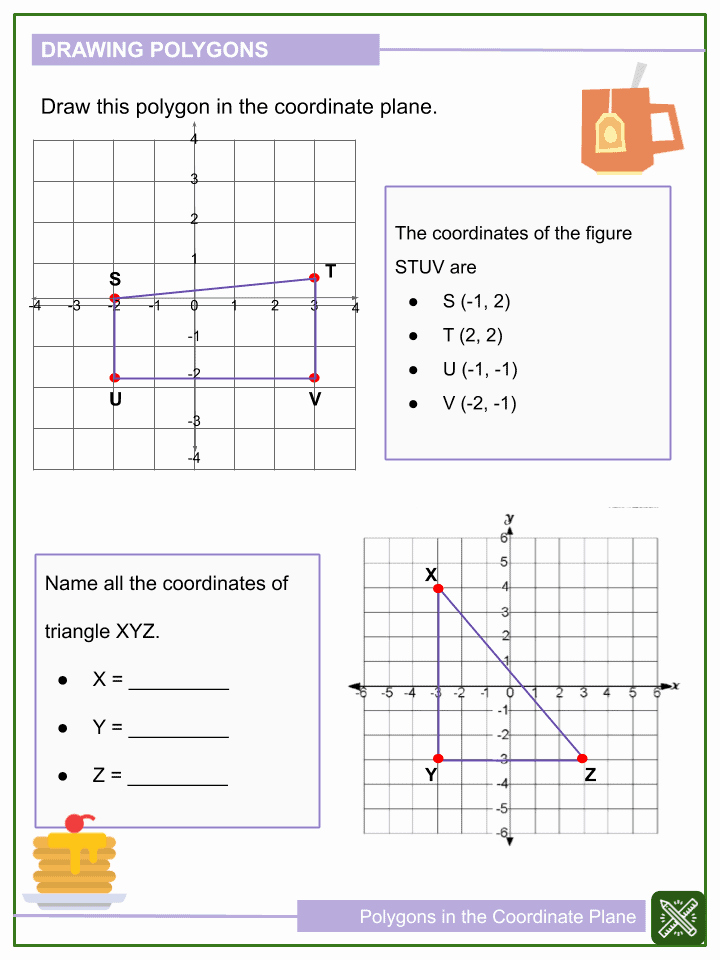
Plotting Points to Create Polygons

To construct polygons, we start by plotting their vertices. Here’s how:
- Identify the vertices: Each vertex must be defined with a specific coordinate pair.
- Plot each vertex: Mark these points on the coordinate plane.
- Connect the dots: Draw straight lines to join the points, forming the sides of the polygon.

Real-World Examples of Polygons
Geometry doesn’t just exist in textbooks; it’s all around us:
- Architecture: From the pentagonal shape of the Pentagon to the octagonal gazebo in a park, polygons shape our environments.
- Art: Artists use polygons to create dynamic compositions, balancing the visual weight with the interplay of straight lines.
- Nature: Observe the hexagonal structure of a snowflake or the almost circular arrangement of leaves on a stem.
Exploring Different Types of Polygons

Polygons come in a variety of shapes, each with distinct characteristics:
- Regular polygons: All sides and internal angles are equal (e.g., square, hexagon).
- Irregular polygons: Sides or angles are not necessarily equal (e.g., kite, scalene triangle).
- Convex polygons: Have no interior angles greater than 180°.
- Concave polygons: Have at least one interior angle greater than 180°.
Mathematical Properties of Polygons

Let’s dive into some key mathematical properties:
- Number of sides: Polygons are classified by their number of sides. A polygon with n sides is an n-gon.
- Perimeter: The sum of the lengths of all sides.
- Area: Calculated differently for each type. For regular polygons, you can use area formulas.
- Sum of Interior Angles: For any polygon with n sides, the sum of the interior angles is (n-2) * 180°.
Transformations of Polygons

Polygons on the coordinate plane can undergo various transformations:
- Translation: Shifting the polygon without altering its shape or orientation.
- Rotation: Rotating the polygon around a point.
- Reflection: Flipping the polygon over a line.
📝 Note: These transformations help in understanding symmetry and visual relationships in design.
Worksheet for Practice

To reinforce your understanding, here’s a printable worksheet:
| Task | Description |
|---|---|
| 1. Plotting | Plot a rectangle with vertices (1,1), (5,1), (5,4), (1,4). |
| 2. Identify | Identify the shape formed by plotting (2,3), (5,7), (2,7), (5,3). |
| 3. Calculate Perimeter | Find the perimeter of a triangle with vertices at (0,0), (4,0), and (2,3). |
| 4. Transform | Reflect the square with vertices at (1,1), (4,1), (4,4), (1,4) over the x-axis. |

📝 Note: Practicing with these exercises will enhance your ability to work with polygons on coordinate planes.
To wrap up, this journey through the coordinate plane and polygons not only equips you with a deeper understanding of geometry but also provides practical exercises to test and reinforce your knowledge. By mastering the plotting and transformation of polygons, you unlock new ways of visualizing and solving geometric problems, which can be applied in various fields from architecture to computer graphics.
What is the coordinate plane?

+
The coordinate plane is a two-dimensional system where points are located by their horizontal (x) and vertical (y) coordinates. The axes meet at a central point known as the origin (0,0).
How do I plot a polygon?

+
To plot a polygon, you identify each vertex by its (x,y) coordinates, plot these points, and then connect them in order to form the sides of the polygon.
What is the significance of understanding transformations in polygons?

+
Understanding transformations (like translation, rotation, and reflection) allows for the manipulation of polygons, which is crucial in fields like computer graphics, engineering, and design for visualizing symmetry and spatial relationships.
Can you explain the difference between convex and concave polygons?

+
A convex polygon has no interior angles greater than 180°, while a concave polygon has at least one angle exceeding 180°, creating an indentation or “cave” within the shape.
Why are polygons important in everyday life?

+
Polygons shape our environment; they’re found in architecture, art, nature, and even in the design of everyday objects, from the shape of signs to the structure of buildings.